Il numero di Nepero è irrazionale.

03/10/18

Il numero di Nepero è irrazionale.

Categorie: Matematica Scritto da: Umberto Cibien Commenti:0

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Eulero e  Nepero si sono  Entrambi occupati del numero e. In realtà, sembra che sia stato  Giacomo Bernoulli, il primo a considerare il numero e come limite della successione \dpi{120} a_{n}= (1+\frac{1}{n})^{n}. Ciononostante, il numero è noto più che altro come numero di Nepero.

Ricordate il problema esponenziale ?  Ad un certo punto della soluzione, diventa necessario capire se il limite:

\dpi{120} \lim_{n \to \infty}(1+\frac{1}{n})^{n} esista e abbia un valore finito.

Facciamolo in due passi.

Primo passo: dimostriamo per prima cosa che la successione :

\dpi{120} a_{n}= (1+\frac{1}{n})^{n}  è strettamente crescente.(\dpi{120} a_{1}<a_{2}<.....<a_{n}<..)

osserviamo che ogni termine è positivo.  Ricordiamo che una successione altro non è che una funzione che ha come dominio l'insieme dei numeri naturali, e come codominio (di solito ) R, insieme dei numeri reali.

N--->R, \dpi{120} n \to a_{n}.  Per prendere un po' di confidenza,  calcoliamo i primi termini della successione:

\dpi{120} a_{1}=(1+\frac{1}{1})^{1}=2

\dpi{120} a_{2}=(1+\frac{1}{2})^{2}=\frac{9}{4}

\dpi{120} a_{3}=(1+\frac{1}{3})^{3}=\frac{64}{27}

già da qui vediamo che la funzione è crescente.

Dimostriamolo però per ogni valore di n ,  usando il  binomio di Newton: (a+b)^{n}=\sum_{k=0}^{n}\frac{n!}{(n-k)!\cdot k!}a^{n-k}\cdot b^{k}.

\dpi{120} \dpi{120} (1+\frac{1}{n})^{n}=\sum_{k=0}^{n}\frac{n!}{k!(n-k)!}\cdot \frac{1}{n^{k}}\cdot 1^{n-k}

\dpi{120} \dpi{120} (1+\frac{1}{n})^{n}=\sum_{k=0}^{n}\frac{n\cdot (n-1)\cdot \cdot \cdot (n-k+1)}{k!}\cdot \frac{1}{n^{k}}

il prodotto \dpi{120} n\cdot (n-1)\cdot \cdot \cdot (n-k+1) ha k fattori, per cui a denominatore possiamo esplicitare \dpi{120} n^{k} ottenendo k frazioni.

\dpi{120} \dpi{120} (1+\frac{1}{n})^{n}=\sum_{k=0}^{n}\frac{1}{k!}\cdot \frac{n}{n}\cdot \frac{n-1}{n}\cdot \cdot \frac{n-k+1}{n}

 

\dpi{120} \dpi{120} a_{n}=\ (1+\frac{1}{n})^{n}=\sum_{k=0}^{n}\frac{1}{k!}\cdot (1-\frac{1}{n})\cdot \cdot \cdot (1-\frac{k-1}{n})

 

vogliamo confrontare  an con an+1; per an+1 avremo dei conti analoghi (basta sostituire a n -->n+1:

\dpi{120} a_{n+1}=\ (1+\frac{1}{n})^{n}=\sum_{k=0}^{n+1}\frac{1}{k!}\cdot (1-\frac{1}{n+1})\cdot \cdot \cdot (1-\frac{k-1}{n+1})

Fissiamo ora un valore di k. Osserviamo che il primo termine \dpi{120} (1-\frac{1}{n}) che compare nella sommatoria di an è minore del primo termine che compare nella sommatoria di an+1: \dpi{120} (1-\frac{1}{n+1}); questo succede per ogni fattore nei prodotti generati con un certo k,  dal primo all'ultimo:  \dpi{120} (1-\frac{k-1}{n})<(1-\frac{k-1}{n+1}). Quindi ogni addendo della sommatoria che dà an è minore del corrispondente che dà an+1. Inoltre, per k=n+1 nella seconda sommatoria  abbiamo un termine in più. Quindi senz'altro \dpi{120} a_{n}<a_{n+1}.

Per vederlo meglio:

\dpi{120} \dpi{120} a_{n+1}=\ (1+\frac{1}{n})^{n}=\sum_{k=0}^{n}\frac{1}{k!}\cdot (1-\frac{1}{n+1})\cdot \cdot \cdot (1-\frac{k-1}{n+1})+ T(n+1))

(ci siamo fermati nella sommatoria a k=n; il termine T(n+1) è il termine che si ottiene per k=n+1, ed è un termine positivo. Possiamo adesso confrontare le due somme , che hanno , fissato k,  solo come differenza  il fatto che in un prodotto compare n, nell'altro n+1:

per \dpi{120} a_{n}:

\dpi{120} \frac{1}{k!}\cdot (1-\frac{1}{n})\cdot \cdot \cdot (1-\frac{k-1}{n})

per \dpi{120} a_{n+1}:

\dpi{120} \frac{1}{k!}\cdot (1-\frac{1}{n+1})\cdot \cdot \cdot (1-\frac{k-1}{n+1})

quindi, per ogni k, essendo n<n+1

\dpi{120} \frac{1}{k!}\cdot (1-\frac{1}{n})\cdot \cdot \cdot (1-\frac{k-1}{n})< \frac{1}{k!}\cdot (1-\frac{1}{n+1})\cdot \cdot \cdot (1-\frac{k-1}{n+1})

e quindi anche per le due sommatorie:

\dpi{120} \sum_{k=0}^{n}\frac{1}{k!}\cdot (1-\frac{1}{n})\cdot \cdot \cdot (1-\frac{k-1}{n})< \sum_{k=0}^{n}\frac{1}{k!}\cdot (1-\frac{1}{n+1})\cdot \cdot \cdot (1-\frac{k-1}{n+1})

il primo membro è \dpi{120} a_{n}, il secondo è \dpi{120} a_{n+1}-T(n+1), con T(n+1)>0 Siamo quindi sicuri che \dpi{120} a_{n}<a_{n+1}

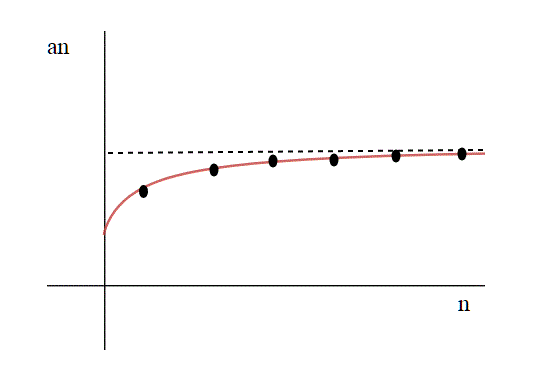
La successione è dunque strettamente crescente.

Secondo passo: la successione degli \dpi{120} a_{n} è compresa fra 2 e 3:

\dpi{120} 2<a_{n}<3 per ogni n>1.

se n=1, \dpi{120} a_{1}=(1+\frac{1}{1})^{1}=2; essendo strettamente crescente, \dpi{120} 2<a_{n} qualsiasi sia n.

Riprendiamo adesso in mano l'espressione \dpi{120} \dpi{120} a_{n}=\ (1+\frac{1}{n})^{n}=\sum_{k=0}^{n}\frac{1}{k!}\cdot (1-\frac{1}{n})\cdot \cdot \cdot (1-\frac{k-1}{n})

essendo ciascuno dei  fattori del tipo \dpi{120} (1-\frac{1}{n}),...\dpi{120} (1-\frac{k-1}{n})  minori di 1, si avrà:

\dpi{120} \dpi{120} \dpi{120} a_{n}=\ (1+\frac{1}{n})^{n}=\sum_{k=0}^{n}\frac{1}{k!}\cdot (1-\frac{1}{n})\cdot \cdot \cdot (1-\frac{k-1}{n})<\sum_{k=0}^{n}\frac{1}{k!}

Notiamo poi che \dpi{120} k!=1\cdot 2\cdot 2\cdot \cdot \cdot k\geq 1\cdot 2\cdot 2=2^{k-1}    d)

\dpi{120} a_{n}<\sum_{k=0}^{n}\frac{1}{k!}=1+\sum_{k=1}^{n}\frac{1}{k!}\leq 1 + \sum_{k=1}^{n}\frac{1}{2^{k-1}}=1 + \sum_{k=0}^{n-1}\frac{1}{2^{k}}

dove abbiamo usato la diseguaglianza  d) nel terzo passaggio ,mentre  nell'ultima sommatoria, se si cambia l'indice da k -1 a k  gli estremi vanno  cambiati  con 0 e n-1 . Ciò ci permette di capire che l'ultima sommatoria è una somma geometrica:

\dpi{120} \sum_{k=0}^{n-1}\frac{1}{2^{k}}=\frac{1-\frac{1}{2^{n}}}{1-\frac{1}{2}}=2\cdot (1-\frac{1}{2^{n}})<2

quindi \dpi{120} \dpi{120} a_{n}\leq 1 + \sum_{k=1}^{n}\frac{1}{2^{k-1}}=1 + \sum_{k=0}^{n-1}\frac{1}{2^{k}}<1+2=3

pertanto \dpi{120} 2<a_{n}<3. Questo ci basta  per concludere che la successione, essendo crescente e limitata, ammette un limite*, che chiamiamo proprio e.  Dunque  \dpi{120} \dpi{120} 2<e\leq 3.

  • In realtà dovremmo citare un noto teorema sulle successioni crescenti e limitate , che afferma proprio quanto detto. Non avendo parlato mai a fondo di successioni, ci limitiamo ad intuire che essendo crescente e limitata superiormente, alla fine dovrà convergere ad un numero limitato. Inoltre questo limite potrebbe anche essere uguale a 3, ma vedremo che è impossibile.
crescente1
Una funzione crescente e superiormente limitata, tende ad un  valore finito. Nel nostro caso la funzione non assume tutti i valori, ma solo quelli relativi ai pallini, essendo appunto una successione. Chiaramente il risultato finale non cambia.

La funzione esponenziale \dpi{120} e^{x}

Due parole sulla funzione esponenziale; siamo talmente abituati ad usarla che forse non ci ricordiamo nemmeno come è definita.  Infatti, finchè si tratta di usare degli esponenti interi o razionali, sappiamo tutti cosa significa \dpi{120} e^{n} , e^{\frac{m}{n}}. Ma quando l'esponente è un numero reale x? Abbiamo visto in questo articolo  come la definì Newton. Come una serie di potenze di cui si ricavò i coefficienti imponendo che la funzione fosse uguale alla sua derivata. Il risultato finale fu questo:

e^{x}= \sum_{n=0}^{\infty}\frac{x^{n}}{n!} . Per quanto appena detto sappiamo poi  che D\dpi{120} e^{x}=e^{x}.

 

Irrazionalità di e

Il numero di Nepero e, definito come  limite della successione

\dpi{120} \dpi{120} \lim_{n \to \infty}(1+\frac{1}{n})^{n}=e

 è un numero irrazionale.

Supponiamo per assurdo che e  sia un numero razionale. Allora  \dpi{120} \dpi{120} \dpi{120} e=\frac{p}{q} con p, q numeri interi.

Sfruttiamo adesso la formula di Taylor, che potete trovare qui nell'archivio. In particolare, siamo interessati allo sviluppo di Maclaurin  con il resto di Lagrange:

f(x) = f(x0) + (x ) f ’(x0) + f ”(x0) (x )2/2 + f III(x0)(x –)3/6 + f IV(x0)(x )4/24 + …. + f n(x0) (x )n /n! + Rn+1

Dove:

Rn+1 = f n+1(xn+1)(x )n+1  /(n + 1)!

Applichiamolo alla funzione \dpi{120} e^{x} (che ha tutti i requisiti)

\dpi{120} \dpi{120} \dpi{120} \dpi{120} e^{x}=1+x+\frac{x^{2}}{2!}+....+\frac{x^{n}}{n!}+ \frac{e^{x_{n}}}{(n+1)!}\cdot x^{n+1} dove 0<xn<x

ponendo x=1, abbiamo:

\dpi{120} e=\sum_{k=0}^{n}\frac{1}{k!}+\frac{e^{x_{n}}}{(n+1)!}     ;0<xn<1

sostituiamo adesso ad \dpi{120} \dpi{120} \dpi{120} e=\frac{p}{q}  e moltiplichiamo ambo i membri per n!:

\dpi{120} \dpi{120} \dpi{120} n!e=n!\cdot \frac{p}{q}=\sum_{k=0}^{n}\frac{n!}{k!}+ \frac{e^{x_{n}}}{n+1}

essendo  0<xn<1, ed essendo crescente la funzione esponenziale, \dpi{120} 1=e^{0}<e^{xn}<e<3, quindi \dpi{120} e^{xn}<3;

Prendiamo adesso n>max(3,q). I numeri n!p/q risulta intero. chiaramente anche il numero n!/k! è intero e quindi anche

la sommatoria  \dpi{120} \sum_{k=0}^{n}\frac{n!}{k!}.  Quindi anche la differenza  \dpi{120} n!\cdot \frac{p}{q}-\sum_{k=0}^{n}\frac{n!}{k!} è un intero. Tale differenza è uguale a \dpi{120} \frac{e^{x_{n}}}{n+1};  ma abbiamo preso n>3, ed essendo \dpi{120} e^{xn}<3, risulta:

\dpi{120} \frac{e^{x_{n}}}{n+1}<1.  Quindi l'identità \dpi{120} \dpi{120} \dpi{120} e=\frac{p}{q} è assurda, e il numero di Nepero non può essere razionale. E quindi e non può nemmeno essere uguale a 3, che è un numero razionale. Quindi 2<e<3.

 

Articoli correlati

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.