Questo articolo fa parte della serie dedicata alla Relatività di Epstein, all'interno della sezione d'archivio  "Relatività Ristretta"

 

Dopo la dilatazione dei tempi, continuiamo con il semplice metodo di Epstein per descrivere la relatività ristretta. Questa volta tocca alla contrazione delle lunghezze e alla mancanza di sincronizzazione di orologi in moto relativo. Applichiamo, infine, il metodo per via puramente grafica per ritornare, ancora una volta, sul paradosso dei gemelli.

Contrazione delle lunghezze.

Ammettiamolo… mentre determinare la dilatazione del tempo è cosa estremamente semplice anche nel diagramma di Minkowski, molto meno lo è la contrazione delle lunghezze. Spesso ci si confonde e ci si fa ingannare da un qualcosa che sembra più lungo e, invece, è più corto (acrobazie della geometria iperbolica…). Adottando il procedimento di Epstein, ogni difficoltà sparisce e la contrazione diventa risultato immediato.

Seguiamo la determinazione con l’esempio della Fig.  5

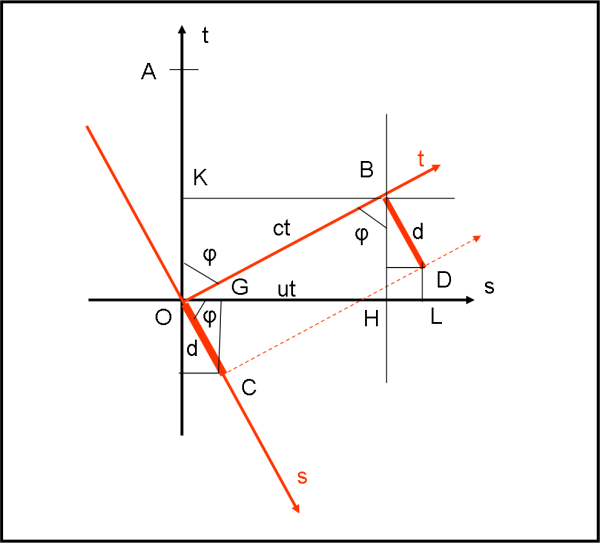
Come al solito (a) è il sistema di riferimento nero e (b) è quello rosso che si muove con velocità spaziale u. Sappiamo subito tracciare l’asse dei tempi rosso e il corrispondente asse dello spazio, ricordando (vedi QUI) che:

u/c = sen φ

Lungo lo spazio di (b) inseriamo un'asta OC di lunghezza d. Essa è ovviamente ferma nel sistema rosso e nel tempo t si sposta, parallelamente a se stessa, in BD. La lunghezza OB vale, come sempre ct. Nello stesso periodo di tempo il punto A di (a) si è spostato lungo l’asse t nero. Si deriva subito, come già descritto precedentemente, che il sistema (a) vede una dilatazione del tempo da parte del sistema (b), infatti mentre A ha percorso il tratto OA, il sistema (b) ha percorso solo OK.

Ma, ciò comporta anche che la lunghezza OB viene vista da (a) proiettata sul suo asse spaziale in OG e quindi (a) non può fare altro che considerare proprio OG la lunghezza dell’asta.  Ricordano che COG = φ, dato che BOG = 90 - φ, è banale scrivere:

OG = OC cos φ          (sen²φ + cos²φ) = 1

quindi  OG = OC √(1 – u²/c²)

Esattamente la (3) relativa ai tempi. In poche parole, il sistema (a) vede una contrazione della lunghezza d che è data dallo stesso fattore moltiplicativo, che altri non è che 1/γ. Ossia:

OG = d’ = d/γ            [ricordiamo che γ  = 1/√(1 – u²/c²) è il fattore di Lorentz]

Immaginiamoci un bel fotone che porti “in mano” un’ asta (priva di massa, ovviamente): bene, per noi avrebbe lunghezza nulla come nullo è il tempo che vediamo scorrere sul suo orologio. Non meravigliamoci più di tanto… il fotone vedrebbe la stesse cose accadere al nostro sistema… e avremmo ragione entrambi!

La perdita di sincronizzazione

Ciò che è simultaneo per un sistema non lo è più per un sistema in movimento rispetto al primo. Questa considerazione fondamentale per tutta la relatività ristretta (relatività della simultaneità), si ricava in modo estremamente facile con il diagramma di Epstein (e non dobbiamo certo stupirci). In realtà, basta usare la Fig. 6 (che è praticamente la Fig. 5) ed effettuare la proiezione sull’asse del tempo nero.

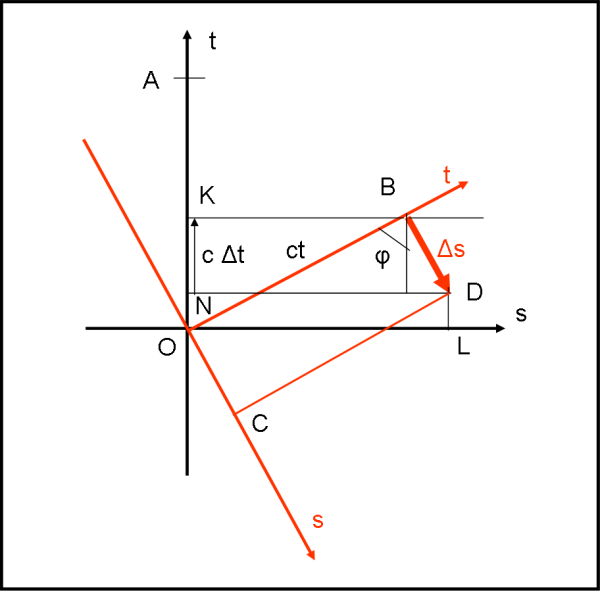
Nel sistema (b) consideriamo due orologi perfettamente sincronizzati (O e C),  come in Fig. 5, che quando arrivano in B e D restano ovviamente sincronizzati nel sistema rosso (ovvero continuano a misurare la stessa ora). Il sistema (a) legge, invece, una differenza di tempo Δt tra i due orologi (segmento . Sia Δs la differenza di spazio nel sistema (b) tra i due orologi. Si ottiene facilmente che:

KN = Δt c = - Δs sen φ = - Δs u/c

Δt = - Δs u/c²

Il segno meno è stato inserito in quanto l’orologio più avanti spazialmente per (b) resta indietro temporalmente per (a).

Ciò che è simultaneo per il sistema rosso non lo è più per quello nero (e viceversa).

Ancora il paradosso dei gemelli

Abbiamo in mano tutte le relazioni fondamentali ed esse possono essere applicate agendo anche soltanto graficamente. Facciamo un caso pratico, descrivendo il paradosso dei gemelli, che sarà anch’esso di un’ovvietà imprevista, solo attraverso un foglio di carta quadrettata.

I due gemelli hanno 25 anni al momento della partenza. Imponiamo che il gemello astronauta (B) viaggi a un velocità di 12/13 di quella della luce. Dopo 26 anni, quando il gemello sedentario (A) compie 51 anni, l’astronauta torna a casa: quanti anni ha?

L’astronauta deve, perciò, allontanarsi dalla terra per 13 anni e poi tornare indietro nel tempo che rimane. Se non tornasse indietro ma continuasse nel viaggio la dilatazione del tempo sarebbe valida per entrambi i gemelli ed entrambi direbbero che è il fratello a rimanere più giovane (avrebbero ragione, ma non potrebbero incontrarsi).

In Fig. 7, utilizziamo solo un foglio a quadretti dove in ascissa ci sono gli anni luce (1 quadretto = 1 anno luce) e in ordinata gli anni (1 quadretto = 1 anno). Gli assi neri si riferiscono al gemello sedentario A.

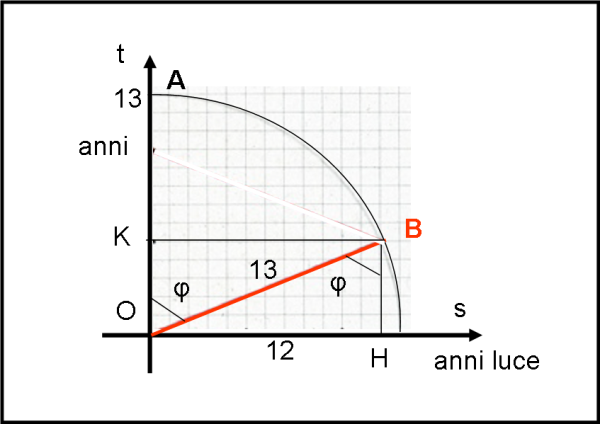
Dobbiamo tracciare l’asse dei tempi rosso del gemello astronauta. Sappiamo che la velocità vale 12/13 di quella della luce, ossia sappiamo che sen φ = u/c = 12/13. bisogna, perciò, disegnare un triangolo rettangolo che abbia come ipotenusa 13 quadretti e come cateto maggiore 12 quadretti.

In pratica, basta tracciare una circonferenza di centro O e raggio uguale a 13 quadretti e poi tracciare la perpendicolare all’asse s  dal punto H, tale che OH = 12 quadretti, fino a incontrare la circonferenza. Quel punto B unito a O indica l’asse dei tempi del gemello viaggiatore (rosso).  Inoltre, sappiamo anche che quando è giunto in B sono ovviamente passati 13 anni di tempo proprio.

E’ immediato determinare quanti anni sono passati per lui nel sistema del fratello nero A. Basta tracciare la perpendicolare da B all’asse dei tempi di A, ossia BK. OK è il tempo che misura il gemello sedentario ed è esattamente uguale a 5 anni. Il gemello A conclude, come è più che logico, che per il gemello astronauta sono passati solo 5 anni, mentre per lui ne sono passati ben 13. Tuttavia, alla stessa conclusione arriverebbe anche il gemello rosso (basterebbe proiettare OA sull’asse OB…).

Giunto in B, però, l’astronauta decide di tornare indietro (Fig. 8 ) e per farlo deve eseguire la stessa traiettoria dell’andata con il segno della velocità u invertita.

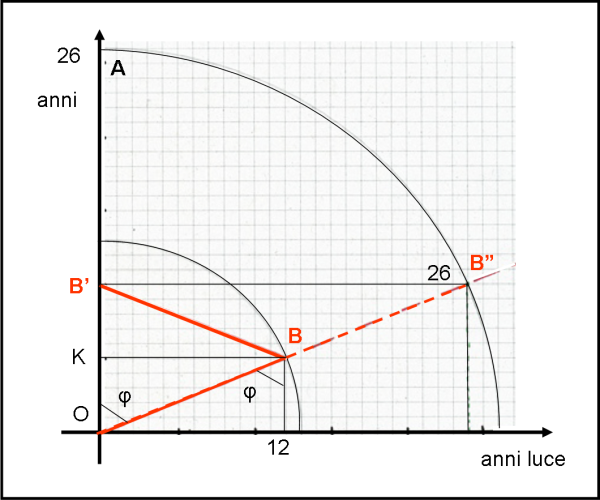
Basta perciò ribaltare il triangolo OBH. In realtà, viene cambiato il sistema inerziale di B e quando torna nel sistema di A (in B’), il tempo passato per lui è veramente di solo 10 anni contro i 26 di A. Non dimentichiamo che tornando sulla Terra -e fermandosi- ritorna a far parte integrante del sistema Terra e il suo orologio inizia a girare come quello di A.

Il sistema inerziale originario di B l’avrebbe portato in B” dopo 26 anni e A avrebbe continuato a misurare il suo tempo come dilatato (sono passati per BB” solo 10 anni se visti da A), ma la stessa identica constatazione la farebbe anche B” rispetto ad A. Nel diagramma si nota anche benissimo che i tempi propri di B” e A sono rimasti identici e pari a 26 anni.

Se volessimo essere più precisi, basterebbe inserire nella figura anche le parti in cui B è costretto ad accelerare e a decelerare. In entrambe le situazioni il suo tempo si dilaterebbe di meno (andrebbe a velocità istantanea inferiore). La Fig. 9 riporta uno schema approssimato di quello che capiterebbe realmente e il diagramma di Epstein non ha nessun problema a rappresentarlo con estrema semplicità e chiarezza.

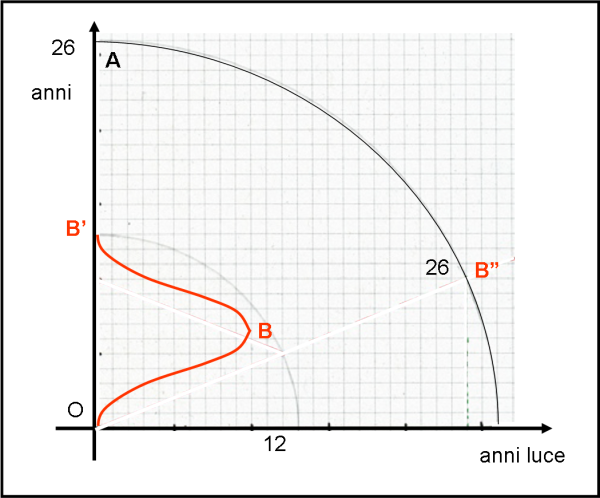
Per raggiungere la velocità di crociera e per poter invertire la rotta l’astronauta sarebbe un po’ meno giovane rispetto al caso del raggiungimento istantaneo della velocità di andata e ritorno. L’importante è che il tragitto da O-B-B’ sia uguale al tragitto OB”. I tempi propri dei due gemelli devono essere uguali

Ridendo e scherzando, abbiamo descritto il paradosso dei gemelli in un modo ancora diverso dal solito e attraverso un diagramma addirittura banale.