Questo articolo è stato inserito nelle pagine d'archivio Dinamica e Meccanica e in Meccanica Quantistica.

 

Per stabilire chi è il vincitore tra Achille e la Tartaruga bisogna normalmente passare al limite oppure farli andare sui campi da sci. Molto più semplice è invece stabilire il vincitore tra una Tartaruga-muone (ad esempio) e un Achille-fotone. E tutto avviene in silenzio senza dover aspettare che venga frantumato il solito muro del suono.

Probabilmente l’inizio di questo articolo sembra essere un po’ strano e confusionario… Cosa c’entrano Achille e la Tartaruga, un muone, un fotone e ìl muro del suono? No, non sto dando i numeri ma sto solo collegando fenomeni molto simili. Cominciamo, perciò, con la nostra strana gara…

Il fotone si sente la particella (in fondo, non lo è nemmeno) più veloce dell’Universo e sfreccia alla sua velocità costante irraggiungibile che indichiamo con la lettera “c” (che sta per celeritas = velocità in latino) ossia la velocità della luce, quasi 300 000 km/s.

Quando il muone-tartaruga  (potevamo scegliere qualsiasi altra particella carica di massa molto piccola) affronta il fotone e gli propone la gara, il piccolo quanto di luce (così è meglio) non può che mettersi a ridere e commentare: “Tu, caro muone ti sei montato la testa dopo che quel tale Einstein ha dimostrato che sei capace di vivere più a lungo di quanto dovresti, solo perché viaggi molto veloce. A parte il fatto che tutto si dimostra ragionando con i due sistemi di riferimento (il tuo e quello di chi ti aspetta sulla Terra) resta sempre il fatto che tu resti sempre una vera tartaruga per me. Comunque accetto la sfida… scegli pure tu il campo di gara!”

Quest’ultima concessione è decisamente fatale per il fotone, dato che il muone decide di gareggiare all’interno di un serbatoio pieno di acqua. Eh sì, il fotone non ha mai studiato molto bene la fisica e non sa, abituato a viaggiare nello spazio praticamente vuoto, che la luce che si propaga in un mezzo che non sia il vuoto rallenta in modo anche sensibile. Non è nemmeno difficile calcolare di quanto si riduce dato che basta conoscere l’indice di rifrazione dell’acqua.

Beh… per chi ha qualche problema di memoria possiamo ricordare che un raggio di luce che passa dal vuoto all’acqua, è costretto ad avvicinarsi alla normale alla superficie di confine tra i due mezzi e il rapporto tra il seno dell’angolo di incidenza nel vuoto (ϑ_i) e quello, più piccolo, del raggio penetrato nell’acqua (ϑ_r) è proprio dato dall’inverso dell’indice di rifrazione dell’acqua (n_r) (considerando, ovviamente, uguale a 1 l’indice di rifrazione nel vuoto n₀). In semplicissime formule (e con l’aiuto della Fig. 1)…

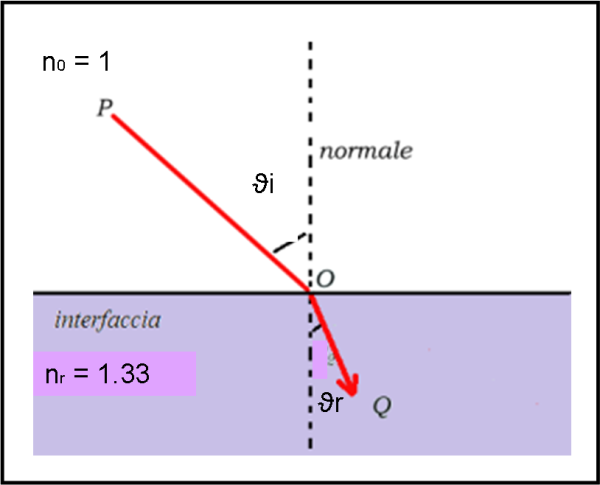
sin ϑ_i/sin ϑ_r = n₀/n_r = 1/n_r

Passando alle velocità, e chiamando c_a la velocità della luce nell'acqua, abbiamo semplicemente che:

c/c_a = n_r/n₀ = n_r

ossia:

c_a = c/n_r

Nel caso dell’acqua (a 20°C)

n_r  ≅ 1.33

e quindi:

ca ≅ c/1.33 ≅ 226 000 km/s

Il muone, invece, può decisamente andare più veloce, pur restando ben al di sotto di 300 000 km/s (lui non andrebbe mai contro al postulato di Einstein sulla velocità della luce nel vuoto).

Insomma, la nostra tartaruga vincerebbe facile e senza bisogno di limiti o trucchi del genere. Tuttavia, la gara deve essere seguita dai giudici e loro hanno bisogno di una prova decisiva sul vincitore, dato che “vedere” la corsa tra un muone e un fotone nell’acqua non è cosa banale.

Alla tartaruga-muone, allora, non resta che spiegare un esperimento abbastanza facile da comprendere che, nel caso lui avesse ragione, farebbe diventare l’acqua di un colore azzurro. Ha anche un nome particolare: EFFETTO CERENKOV.

Tuttavia, si rende conto che la giuria ha delle basi molto limitate a riguardo ed è abituata ad assistere a gare tra oggetti ben visibili e a fenomeni ben cronometrabili… Il muone si vede costretto a spiegare un effetto molto simile, ma ben osservabile nel mondo di tutti giorni: il superamento del muro del suono.

Il muone comincia a spiegare che quando un aereo si muove nell’aria causa, attraverso l’urto con le particelle che la costituiscono, delle onde di pressione  che si propagano con la velocità del suono nell’aria. Se l’aereo va relativamente piano, si assiste al ben noto effetto doppler, ossia chi lo vede arrivare verso di lui sente  le onde con una frequenza maggiore di chi lo vede allontanarsi (basta sentire un’ambulanza che passa vicino e notare la differenza di suono mentre si avvicina e mentre si allontana).

Fin qui tutto bene… ma, adesso aumentiamo la velocità dell’aereo fino a farlo arrivare e a superare la velocità delle onde sonore. Le onde che emette si accavallano tra loro e alla fine è l’aereo che si trova davanti a un treno di onde che lascia dietro di sé. Ciò che succede per varie velocità lo vedete in Fig. 2,

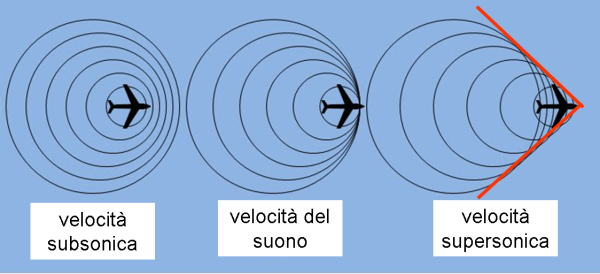
mentre ciò che avviene al superamento della velocità del suono si può vedere nel video di Fig. 3.

 

La compressione dell’aria in queste condizioni  si manifesta lungo un vero e proprio cono che ha l’aereo nel suo vertice. Questo cono produce un “boom”, un suono violento che non è udibile dal’aereo, ma da tutti coloro che vengono investiti dal cono.

Se si è a terra, si sente il boom dove il cono interseca il terreno, come è mostrato in Fig. 4.

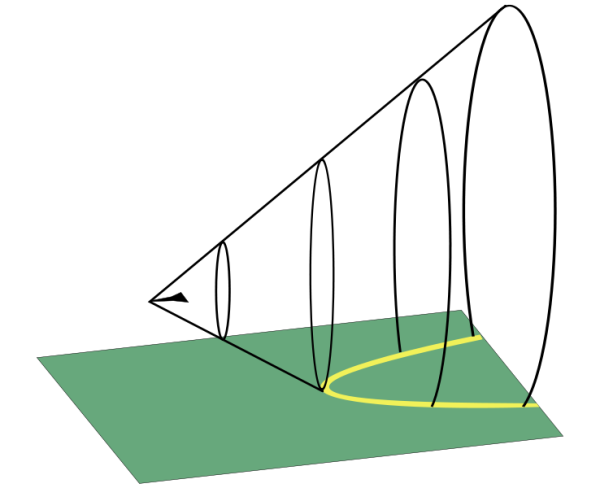
L’effetto del superamento del muro del suono (ossia il momento in cui la velocità dell’aereo supera la velocità del suono nell’aria) si vede anche chiaramente attorno all’aereo dove è più evidente la compressione delle onde acustiche, ossia della propagazione delle particelle spostate (Fig. 5)

I giudici annuiscono, anche se gli occhi di qualcuno sembrano indicare che è la prima volta che sentono questo discorso. Alla fine, però, sono tutti d’accordo sul fenomeno e sono tutti pronti a seguire il seguito della storia. Il fotone, che non è certo un attore dell’Universo senza esperienza, ma che non ha molto tempo per riflettere dovendo sempre andare alla massima velocità possibile, comincia a subdorare qualcosa e comincia a perdere molta della sua sicurezza.

Il muone passa, finalmente, alla sua sfida e inizia il discorso in modo molto simile al caso precedente: “Immaginiamo che io penetri nell’acqua con una velocità inferiore a quella della luce. Creo un po’ si scompiglio, ma niente di speciale, dato che i colpi che do alle molecole e ai loro atomi non producono problemi duraturi e tutto torna, immediatamente, alla situazione precedente.

Tuttavia, se la mia velocità è superiore a quella della luce nell’acqua, il mio effetto sugli atomi incontrati dà luogo a una polarizzazione e all’emissione di raggi gamma, ossia dei veri e propri fotoni, che non possono che viaggiare alla loro velocità. In poche parole, il mio passaggio crea un treno d’onde simili a quelle acustiche dell’aereo. Anch’io sono capace di portarmi dietro un un “cono” di onde, andando più veloce di quanto esse si propagano (Fig. 6).

Queste onde che si propagano dimostrano che io sto proprio andando più veloce di loro e tutto ciò si nota benissimo perché questa radiazione creata dalla mia maggiore velocità tinge di azzurro l’acqua. Guardate cosa succede a quella in cui è immerso un reattore nucleare e dite se non è un effetto ben visibile (Fig. 7)!

 

Ciò che succederà nella gara sarà lo stesso che capita quando si vogliono scoprire i neutrini… Loro sono tra le particelle più timide ed elusive dell’Universo. Tuttavia, siamo molto amici e quando uno di loro entra nell’acqua  preferisce trasformarsi in me (durante l'interazione neutrino-protone o neutrone), molto meno pauroso di mettermi in mostra. Avendo velocità maggiore di quella della luce produco l’effetto Cerenkov e permetto di individuare il passaggio di un neutrino. Ovviamente, la faccenda è un po’ più complicata, ma per voi reputo che sia più che sufficiente: nessun colore vince il fotone, colore azzurro vinco io!”.

Tutti sono pronti alla gara, ma il fotone dà un chiaro segno di umiltà e ammette che il risultato è decisamente segnato dalla logica della fisica. Si ricorda di vecchi discorsi sentiti da suoi fratelli di altre lunghezze d’onda e di ben più grande esperienza e ammette la sua sconfitta. Stringe la mano al muone–tartaruga, saluta e ringrazia i giudici che, in fondo, in fondo, erano piuttosto ansiosi di vedere quella suggestiva luce azzurra. Quindi va a cercare un vecchio testo che spiega il tutto in modo molto più accurato, utilizzando le assurde e fantastiche regole della meccanica quantistica dove si spiega perché  anche la luce ha i suoi problemi quando deve attraversare qualcosa che non sia il vuoto:

“… Il fatto che l’ampiezza finale, dopo la trasmissione attraverso il vetro, ruoti rispetto a quella del passaggio senza scattering (percorso diretto, come se vi fosse solo aria), crea l’impressione che il vetro ritardi il passaggio della luce (ossia la luce impieghi più tempo). In realtà, questo effetto è dovuto alla rotazione e all’accorciamento della freccia a causa dello scattering. Questa capacità di “rallentamento” dovuto alla minore o maggiore inclinazione della freccia finale si chiama indice di rifrazione del materiale. Lo stesso effetto si ottiene, ovviamente, aumentando lo spessore del vetro, dato che si sommano più freccette e la direzione finale si piega di più. Questo è il vero fenomeno su cui si basa una lente, che utilizza uno spessore variabile. In parole semplici, dato che la freccia finale ha una certa inclinazione rispetto a quella senza scattering (ossia quella prima dell'entrata nel vetro) si conclude che essa deve essere partita a un tempo diverso rispetto a quello dell'ampiezza senza scattering. Tempo diverso vuol dire più tempo per raggiungere il rivelatore... e il gioco è fatto: la luce sembra viaggiare più lentamente…”

Per saperne di più si legge con molta calma e attenzione la QED di quel genio indiscusso che è Richard Feynamn e capisce perché anche la luce deve sottostare a certe leggi capaci di non renderla sempre vincente!

Anche i fotoni sono creature dell’Universo e non sono superiori a nessuno.

P.S.: la maggior parte delle figure sono state recuperate da Wikipedia