Categorie: Relatività
Tags: Minkowski Minkowski per tutti Non quiz relatività ristretta relatività speciale simultaneità sistema di riferimento visione diretta
Scritto da: Vincenzo Zappalà
Commenti:9
Minkowski per tutti. 1: Le cinque supernove **
Questo quiz-non quiz fa parte della serie "Minkowski per tutti". La soluzione è inserita in questo stesso articolo, ma sarebbe più interessante provare, prima di leggerla, a darla nei commenti, anche solo per esprimere le eventuali difficoltà incontrate.
Non voglio sicuramente ricominciare a trattare la relatività ristretta che trova ampio spazio nell'archivio. Tuttavia, avendo visto che lo spaziotempo di Minkowski è l'articolo più letto del nostro Circolo, mi è sembrato giusto tastare un po' il polso dei lettori che l'hanno affrontato. Per far ciò, vorrei presentare qualche esercizio di grande semplicità, ma sufficiente a mettere alla prova le conoscenze raggiunte, soprattutto nelle questioni fondamentali: chiamerò questa serie "Minkowski per tutti". Conoscendo la reticenza dei più nell'uscire allo scoperto, non mi aspetto molte risposte "pubbliche", ma sono sicuro che privatamente molti cercheranno di risolverli. Le risposte si possono ottenere schiacciando su "mostra risposta", ma... chi è relativamente speciale non lo farà di certo!
Questo e i prossimi esercizi hanno due asterischi. Ovviamente, i due asterischi si riferiscono a chi si è già costruito le basi della relatività ristretta.
Premessa: simultaneità per un sistema e per un singolo "personaggio" del sistema.
Questo primo esercizio (ma anche gli altri) si basa soprattutto sulla differenza sostanziale che esiste tra ciò che accade in un sistema di riferimento e ciò che vede un certo "personaggio" appartenente al sistema di riferimento (abbiamo già avuto problemi a riguardo...). Nel primo caso l'evento è un qualcosa di comune a tutto il sistema, nel secondo l'evento tiene conto della particolare posizione spaziotemporale del personaggio in questione. Cerco di spiegarmi ancora meglio, richiamando il significato di sistema di riferimento. Consideriamo per esempio quello della Terra. Se trascuriamo i movimenti relativi tra il Sole, i pianeti, le stelle rispetto al nostro pianeta (lo possiamo fare perché stiamo trattando con fenomeni in cui la velocità è nettamente superiore a quelle tra i corpi celesti) il sistema Terra non vuole certo dire solo il pianeta Terra, ma tutto il sistema che si muove solidamente con lui.
In particolare, se lo consideriamo come sistema in quiete, saranno in quiete tutti gli oggetti del firmamento e tutti gli orologi (immaginati presenti in qualsiasi luogo del sistema) saranno sincronizzati tra loro. Ne segue che tutti gli eventi che hanno lo stesso valore della coordinata tempo sono simultanei nel sistema, qualsiasi sia la loro reciproca distanza spaziale. Detto in altre parole, esiste un ordine cronologico ben preciso degli eventi, indipendentemente dalla loro posizione spaziale.
Consideriamo la Fig. 1, in cui vi è il sistema di riferimento terrestre S considerato in quiete, con il suo asse del tempo e il suo asse dello spazio.
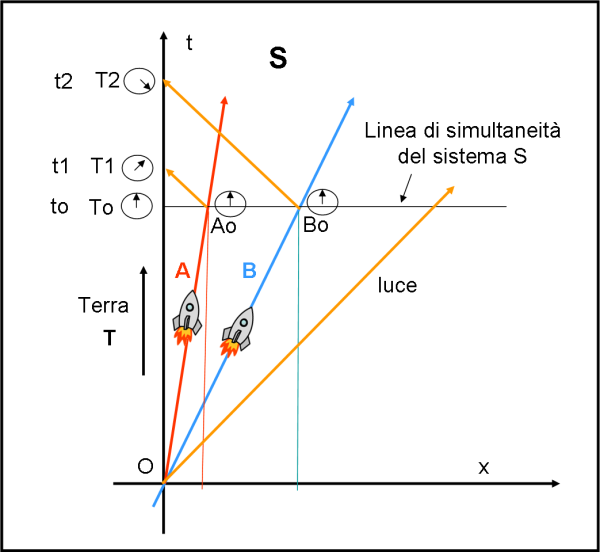
All'istante O partono due astronavi A e B, con velocità diverse. Contemporaneamente si muove anche la Terra T lungo la sola direzione del tempo. Le astronavi attraversano lo spazio ma istante per istante sono "controllate" da un orologio che è perfettamente sincronizzato con quello della Terra T. Ciò succede malgrado le astronavi si allontanino sempre di più dalla Terra intesa come singolo personaggio. In parole estremamente semplificate, se tiriamo una retta perpendicolare all'asse del tempo terrestre, blocchiamo una serie di eventi relativi alle due astronavi, e alla Terra stessa, che avvengono tutti in modo simultaneo, dato che gli orologi posti lungo quella retta segnano per definizione la stessa identica ora (T0, A0 e Bo).
In queste condizioni possiamo dire che ci stiamo riferendo a una simultaneità relativa a un sistema di riferimento ben definito.
Consideriamo, adesso, la faccenda sotto un altro punto di vista. Vogliamo definire gli eventi non rispetto al sistema di riferimento della Terra, ma rispetto al personaggio Terra. In altre parole, definiamo come evento quello in cui la Terra VEDE un certo fenomeno. In questa situazione tutti gli eventi simultanei nel sistema non possono più trascurare la loro distanza dalla Terra. Affinché la Terra riesca a vedere gli eventi simultanei nel suo sistema è necessario che la loro luce la raggiunga nello stesso istante. Immaginiamo, ad esempio, che nel momento in cui si verificano i vari eventi simultanei nel sistema Terra, parta un lampo di luce. Come sappiamo la luce viaggia a 45° in qualsiasi sistema di riferimento (assumendo come coordinate l'anno e l'anno luce), obbedendo a uno dei postulati della teoria stessa.
L'evento più vicino alla Terra, simultaneo nel sistema Terra a To, è Ao: il suo segnale arriva sulla Terra intesa come singolo personaggio in T1, al tempo t1. T1 non è più un evento simultaneo con T0. L'evento più lontano, sempre simultaneo nel sistema Terra a T0 è B. Il suo segnale arriverà sul personaggio Terra solo al tempo t2, posteriore a t1. T2 non è simultaneo con To e T1. La luce non ha velocità infinita...
Possiamo concludere che nel sistema di riferimento della Terra gli eventi T0, A0 e B0 sono simultanei, ma il personaggio Terra vede gli eventi in ordine cronologico diverso: prima T0, poi A0 (quando è in T1) e poi B0, quando è in T2.
Non confondiamo quindi eventi simultanei in un sistema di riferimento e eventi simultanei in quanto visti nello stesso identico istante da un personaggio facente parte del sistema.
Non ci resta che proporre un semplice esercizio che serva come conferma della propria comprensione. Ovviamente, per eseguirlo bisogna conoscere come si trasformano i sistemi di riferimento nel diagramma di Minkowski, ma questo lo devo dare come concetto assodato...
Le cinque supernove
Nel diagramma spaziotemporale di Minkowski sono segnati 5 eventi molto importanti: 5 supernove, indicate con A,B,C,D ed E, nella Fig. 2. Ovviamente, questi straordinari eventi sono osservati da tutti i telescopi terrestri, ma anche dagli scienziati a bordo di un astronave la cui traiettoria è anch'essa segnata nello spaziotempo della figura.
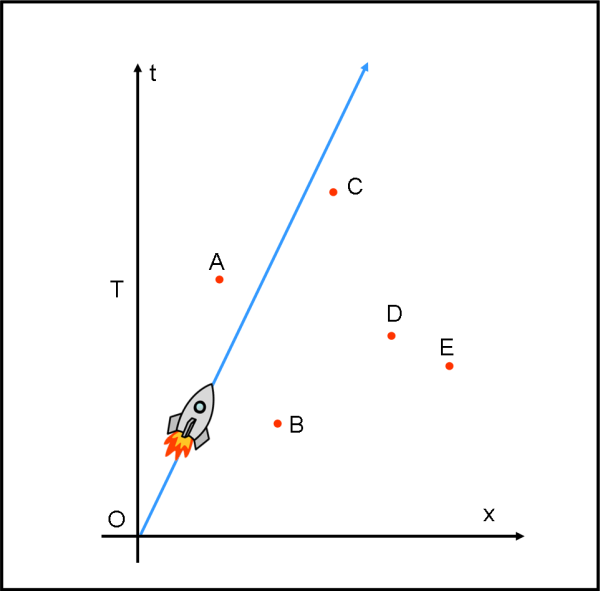
Si chiedono le risposte alle seguenti domande:
- In che ordine cronologico scoppiano le supernove nel sistema di riferimento della Terra?
- In che ordine cronologico scoppiano le supernove nel sistema di riferimento dell'astronave?
- In che ordine cronologico sono viste scoppiare le supernove dalla Terra?
- In che ordine cronologico sono viste scoppiare le supernove dall'astronave?
Gli amanti del quiz, possono dare le loro risposte nei commenti, gli altri non devono fare altro che cliccare sui successivi pulsanti e togliersi subito la curiosità!
Chi è arrivato fin qui può tranquillamente rispondere a un'altra facile domanda:
Quali stelle progenitrici delle nostre cinque supernove potrebbero essere raggiunte, partendo da O, prima di scoppiare, anche facendo cambiare rotta alla nostra astronave?
La serie completa dei quiz - non quiz dedicati al diagramma di Minkowski la trovate QUI






9 commenti
W Epstein.
ma dai... non è vero! Basta avere pazienza, ragionare con calma e poi uno entra nell'ottica relativistica. E' il modo migliore per capire la simultaneità relativa e per non cadere più nel mix tra tempo luce e sistemi di riferimento... Insisti e vedrai che partite farai!!!!
ATTENZIONE LEGGERE SOLO DOPO AVER TENTATO DI RISOLVERE IL QUIZ, ALTRIMENTI LA LETTURA PUO’ NUOCERE GRAVEMENTE ALLA SALUTE DEI NEURONI.
Caro Enzo, prima di rispondere alle domande vorrei fare alcune premesse.
Per indicare graficamente quando tutti gli orologi sincronizzati del sistema di riferimento della Terra segnano lo stesso tempo basta tracciare delle linee parallele all’asse X.
D’altronde l’asse X è definito come l’insieme dei punti aventi la medesima coordinata temporale zero, ossia con t =0 (nel caso di diagrammi cartesiani con coordinata y=0).
E’ un po’ come se avessimo una serie di amici solidali con il sistema di riferimento terrestre dotati di orologi sincronizzati fra loro… tutti gli orologi degli amici solidali con la Terra che si trovano sulla medesima linea parallela all’asse X segnano il medesimo tempo.
Detto in altre parole, questa misura del tempo riferito al proprio sistema di riferimento tiene conto che la luce ha velocità finita.
Pertanto se a 1000 anni luce scoppia una supernova, la luce dell’esplosione arriverà sulla Terra dopo 1000 anni ed in tal caso i terricoli vedono ciò che è accaduto 1000 anni prima.
Anche l’astronave ha un suo sistema di riferimento, diverso da quello terricolo ed anche quel sistema di riferimento ha un’asse X’, caratterizzato dal medesimo tempo, ossia t’=0.
Ovviamente, nel diagramma di Minkowski, l’asse X’, al fine di garantire che la velocità della luce sia sempre la stessa indipendentemente dal sistema di riferimento, avrà la stessa inclinazione (stesso angolo) rispetto all’asse X, di quella, dell’asse t’ rispetto all’asse t (così la luce, il cui angolo è di 45°, si troverà sempre al centro di questi due assi).
Anche in questo caso è un po’ come se avessimo una serie di amici solidali con il sistema di riferimento dell’astronave (per esempio una serie di astronavi che viaggiano alla stessa velocità con la stessa direzione e verso, per cui mantengono sempre la stessa distanza fra loro, ossia sono solidali tra loro) dotati di orologi sincronizzati fra loro… tutti gli orologi degli amici solidali con l’astronave che si trovano sulla medesima linea parallela all’asse X’ segnano il medesimo tempo.
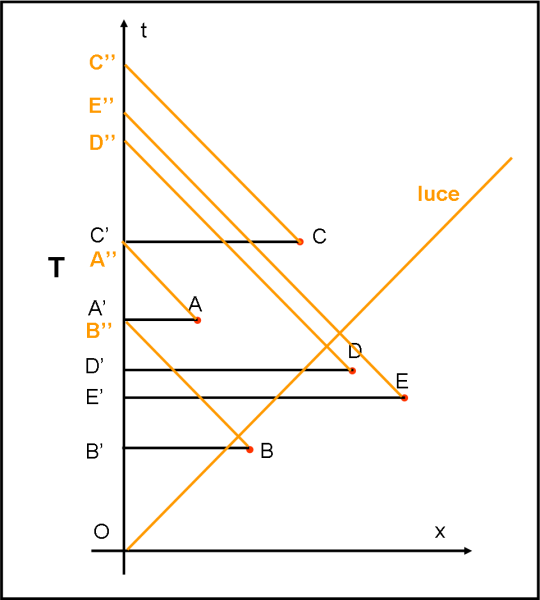
Nella figura 1 sono state tracciate delle linee, passanti per i vari eventi, parallele all’asse X (in nero) dove gli orologi terricoli segnano tutti lo stesso tempo t, ed altre parallele all’asse X’ (in blu), dove gli orologi delle astronavi solidali tra loro segnano tutti lo stesso tempo t’.
Dato che il tempo scorre in unica direzione (dal basso verso l’alto) guardando dove le linee parallele all’asse X incrociano l’asse del tempo t, è facile ricostruire l’ordine cronologico delle esplosioni di supernove secondo il sistema di riferimento terricolo: B; E; D; A; C.
Cambiando sistema di riferimento, ossia considerando il sistema di riferimento delle astronavi, guardando dove le linee parallele all’asse X’ incrociano l’asse del tempo t’, è facile ricostruire l’ordine cronologico delle esplosioni di supernove secondo il sistema di riferimento delle astronavi solidali tra loro: E; B; D; A; C.
Come è facile notare, le esplosioni delle stelle E e B sono cronologicamente invertite cambiando sistema di riferimento… d’altronde ogni sistema ha il suo tempo.
Ancor più facile è rispondere alle domande 3 e 4, poiché basta considerare solo il tragitto compiuto dalla luce partita dalle esplosioni di supernove e vedere quando questa raggiunge chi si trova sulla Terra e chi si trova sull’astronave.
Questa volta non è necessario costruire un sistema di riferimento con tanti amici solidali dotati di orologi sincronizzati tra loro (sincronizzati solo per il proprio sistema di riferimento, ma non per altri sistemi), poiché ci interessa solo sapere cosa vede un terricolo e cosa vede un astronauta.
Nella figura 2, la luce (che nel diagramma di Minkowski viene rappresentata come una linea a 45°) interseca l’asse del tempo terrestre t, secondo il seguente ordine cronologico: B; A; D, E; C.
Pertanto il terricolo vede esplodere prima la supernova B, poi la A, poi la D, la E e infine la C.
La sequenza è mutata rispetto alla cronologia indicata dal sistema di riferimento terrestre, ma d’altronde l’osservazione del terricolo non tiene conto della velocità della luce, dato che si limita a considerare solo quando questa arriva.
Per capire meglio questo semplice concetto, basta pensare a due diverse supernove, una posta a 100 anni luce e l’altra a 1000 anni luce, anche se la luce delle due esplosioni arriva sulla Terra nello stesso istante le due stelle non sono certe esplose nel medesimo momento.
Per quanto riguarda l’astronauta, basta vedere quando la luce raggiunge l’asse del tempo t’, da cui si ricava cosa vede l’astronauta e il conseguente ordine cronologico delle esplosioni: B; D; E; A; C.
Ovviamente tale ordine cronologico è diverso sia da quello misurato dal sistema di riferimento delle astronavi, sia da quello visto dal terrestre.
Infine è semplicissimo rispondere all’ultima domanda.
Le stelle, che in un certo istante esplodono, sono solidali con il sistema di riferimento terrestre (tale approssimazione è valida considerato che non si muovono certo a velocità relativistiche rispetto alla Terra e possono quindi essere considerate quasi “ferme”), pertanto nel sistema terricolo si muovono solo nel tempo, ossia lungo linee parallele all’asse t.
Pertanto tali stelle, nel loro “movimento temporale”, saranno caratterizzate da un passato pre evento esplosione (linea tratteggiata verde) e da un futuro post evento esplosione (linea tratteggiata fucsia).
Ammettiamo di usare un’astronave che viaggia quasi alla velocità della luce (99,9 %).
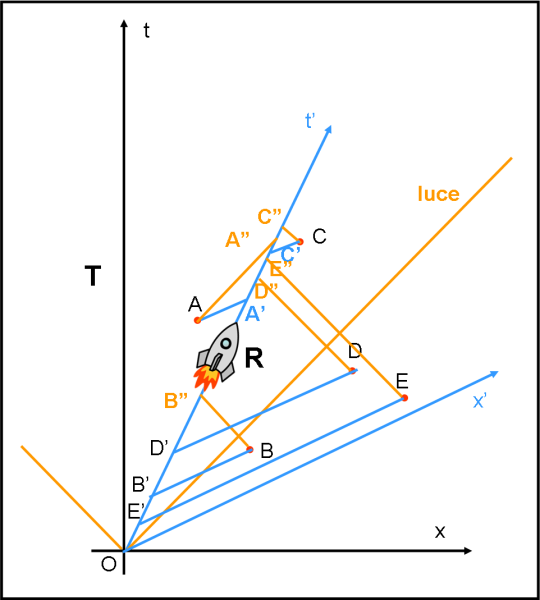
Come mostra la figura 3, l’astronave che si muove lungo l’asse del tempo t'', interseca le stelle A e C prima della loro esplosione (vedi i due pallini verdi che congiungono l’asse del tempo t'' alle linee tratteggiate verdi), mentre interseca le altre tre stelle solo dopo la loro esplosione (l’asse del tempo t'' interseca solo le linee tratteggiate fucsia dopo l’esplosione).
Ciò significa che per quanto veloce possa viaggiare l’astronave è impossibile raggiungere le stelle B; D; ed E prima che esplodano, poiché bisognerebbe viaggiare più veloci della luce…
Paolo
Seguite il consiglio di Paolo!!!! :-)
Intorno alla risposta 2
La risposta la capisco se devo intendere che il cono di luce dell'astronave è compreso fra la retta della luce disegnata come bisettrice dell'angolo fra gli assi x,t del sistema di riferimento terricolo ed una seconda retta della luce, per l'astronave, da disegnare simmetricamente rispetto all'asse t' ...
o sbaglio?
Ciao, una volta che hai tracciato il cono di luce che parte da O non ti serve altro, dato che l’astronave parte da O.
Gli eventi B; D ed E (esplosioni supernove delle tre stelle) si trovano a destra della retta bisettrice tra gli assi x e t, che indica il percorso della luce che parte da O (parte destra del cono di luce), per cui per raggiungerle prima della loro esplosione bisognerebbe viaggiare più veloci della luce e ciò è impossibile.
Paolo
Grazie. Ma io non so disegnare il cono di luce dell'astronave.
Vedo un solo lato, l'altro dove è?
Ciao guarda la figura 4 dell'articolo (inserita nella risposta 1), da O (origine degli assi x e t) vedi a destra la retta bisettrice gialla che indica la parte destra del cono di luce ed a sinistra sempre da O parte un'altra retta gialla che graficamente è sviluppata solo per un breve tratto.
Il cono di luce del'evento O (partenza dell'astronave) è quello compreso tra queste due rette gialle .
Tutto ciò che è all'interno del cono di luce è raggiungibile (partendo da O) senza superare la velocità della luce, tutto ciò che è all'esterno NO!
Ciò significa anche che gli eventi all'interno del cono di luce possono essere anche connessi tra loro (l'informazione ha avuto il tempo di trasmettersi da un evento all'altro), mentre gli eventi all'esterno del cono di luce non possono essere connessi tra loro (l'informazione non può viaggiare più veloce della luce, per cui non ha avuto il tempo di arrivare).
Paolo
grazie Paolo, ormai per te la RR è come un panino al prosciutto. Te la mangi in un boccone!!