Categorie: Relatività
Tags: quiz non quiz relatività speciale sistemi di riferimento velocità relativa
Scritto da: Vincenzo Zappalà
Commenti:12
Ancora relatività speciale: la capsula, il modulo e l'astronave **
Un altro semplice esercizio di relatività speciale. Qualche piccolo calcolo e via!
Perché battere tanto sulla RR? Perché è fondamentale... Basti pensare che la stessa RG deve utilizzarla per determinare le sue regole fondamentali. Gli orologi vengono visti rallentare se la gravità aumenta? Ovvio... La gravità è un'accelerazione, ossia un continuo cambiamento della velocità. L'unica differenza è che solo l'orologio che sente la gravità viene visto rallentare da lontano, mentre chi guarda non viene accelerato e quindi il suo orologio non viene visto rallentare, anzi accelera, se è visto da chi subisce la gravità. Non c'è simmetria. Banale (quasi)...
Solo se si capisce la RR si può entrare nella RG.
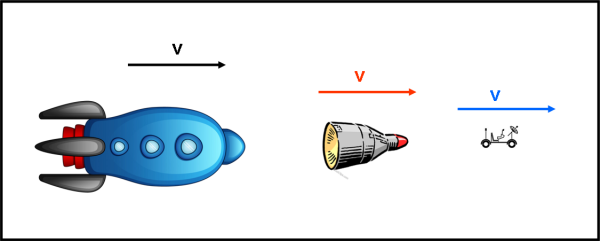
Un’astronave A è partita dalla Terra e viaggia alla velocità v verso un certo pianeta P. A un certo istante dall’astronave viene espulso un modulo B, munito di sensori speciali, che si muove nella stessa direzione dell’astronave con una velocità v rispetto all'astronave A. Giunti nei pressi di P, dal modulo viene lanciata una capsula C diretta proprio verso il pianeta (un robottino?) con la stessa velocità v rispetto al modulo B.
Qual è la velocità della capsula C rispetto alla Terra ?
RISPOSTA
Chi vuole conoscere subito la risposta, non deve fare altro che schiacciare "mostra risposta" (invitiamo, però, chi conosce le basi della RR a provare, prima, da solo...)






12 commenti
Caro Enzo, diciamo che se avessimo posto la medesima domanda a Galileo, avrebbe risposto sommando le tre velocità, ossia V (da Terra) = V + V + V = 3V.
Einstein, però, non sarebbe per nulla d’accordo su questa soluzione, soprattutto se si tratta di velocità che si avvicinano a quelle della luce.
Il motivo è semplice, la velocità della luce non è superabile ed è la stessa per qualunque sistema di riferimento, ossia: per la Terra, per l’astronave, per il modulo B e per la capsula C.
Ammettendo che V sia uguale a 0,5 C, secondo Galileo la capsula per la Terra dovrebbe viaggiare più veloce della luce, ossia a 1,5 c
V (da Terra) = 3 V = 3 x 0,5c = 1,5 c
E’ quindi necessario applicare la composizione relativistica delle velocità
http://www.infinitoteatrodelcosmo.it/2015/06/08/composizione-relativistica-delle-velocita/
A mio avviso, la prima cosa da fare è vedere qual è la velocità della capsula C secondo l’astronave, applicando la formula della composizione delle velocità relativistiche (limitatamente alla direzione del moto, ossia senza considerare le direzioni spaziali y e z).
U = U’ + V / (1 + U’V/C²)
Per l’astronave: U è la velocità della capsula, V la velocità del modulo B, U’ la velocità della capsula secondo il modulo B.
Nel quiz si dice che U’ è uguale a V, quindi:
U (per l’astronave) = V + V/ (1 + VV/C²)) = 2V/(1 + V²/C²).
Ricordando che ß= V/C, si può semplificare:
U (per l’astronave) = 2V/(1 + ß²).
Questa è la velocità della capsula, misurata dal sistema di riferimento dell’astronave, ma il quiz chiede di trovare la velocità della capsula secondo la Terra.
Di nuovo occorre applicare la formula delle composizione relativistica delle velocità.
Questa volta U è la velocità della capsula secondo la Terra, U’ la velocità della capsula secondo l’astronave e V è la velocità dell’astronave secondo la Terra.
Precedentemente abbiamo trovato che la velocità della capsula secondo l’astronave, ora indicata come U’, era uguale a 2V/(1 + ß²), quindi non resta che sostituirla nella formula:
U = U’ + V / (1 + U’V/C²)
U (per la Terra) = (2V/(1 + ß²)) + V / (1 + (2V/(1 + ß²)) V/C²)
U (per la Terra) = (2V + V(1 + ß²)/(1 + ß²)/(1 (1 + ß²) + (2VV))/C²(1 + ß²)
U (per la Terra) = (2V + V + Vß²)/(1 + ß² + 2(V²/C²))
U (per la Terra) = (3V + Vß²)/(1 + ß²+ 2 ß²)
U (per la Terra)= V (3 + ß²)/(1 + 3ß²)
Nel caso di velocità non relativistiche, dato che V è molto, molto più piccola di C, ß =V/C ≃ 0
Sostituendo a ß il valore zero, si ottiene il risultato che avrebbe fornito Galileo:
U = V (3 + 0²)/(1 + 3 x 0²) = V (3 +0)/(1 + 0) = 3V/1 = 3V
Come si può notare la composizione relativistica delle velocità consente sia di evitare risultati assurdi con velocità superiori a quelle della luce, sia nel caso di velocità trascurabili rispetto a quelle della luce, lo stesso risultato della relatività Galileiana (basta pensare che un razzo che viaggia a 36.000 km/h, viaggia solo a 10 Km/s e quindi a un trentamillesimo della velocità della luce ).
).
Paolo
Buongiorno, io risolverei nel seguente modo:
Supponendo che il modulo B venga lanciato dall'astronave in quiete rispetto alla Terra per ottenere la velocità del modulo C rispetto alla Terra compongo relativisticamente le velocità del modulo B (che chiamo VB) e di C (che chiamo VC), ottenendo la velocità della capsula C rispetto alla Terra (che chiamo V'C):
V'C=(VB+VC)/(1+VBVC/c^2) (1) formula della composizione relativistica delle velocità applicata considerando che B e C abbiano il vettore velocità avente medesima direzione
ma, poichè il problema pone VA=VC, la relazione (1) diviene:
V'C=(2VB)/(1+VB^2/c^2) (2)
V'c così ottenuta ha sempre la stessa direzione di VB e di VC.
Poichè però il modulo B è stato lanciato dall'astronave che ha velocità VA rispetto alla Terra occorre nuovamente applicare la composizione relativistica della velocità della capsula C rispetto alla Terra ottenuta dalla (2) con la velocità dell'astronave rispetto alla Terra:
V"C=(VA+V'C)/(1+VAV'C/c^2) (3) formula della composizione relativistica delle velocità applicata con V'c e VA aventi medesima direzione
ma la relazione (2) posso scriverla sostituendo VA al posto di VB perchè il problema le pone uguali. Così fatto la (3) diviene:
V"C=(VA+(2VA/(1+VA^2/c^2))/(1+(2VA^2/(1+VA^2)/c^2)c^2)
Se non ho poi sbagliato i calcoli (cosa invece probabile...) si arriva alla fine al risultato:
V"C=VA(3c^2 + VA^2)/(c^2 + 3VA^2) (4)
Mi sembra che la (4) per valori di VA piccoli (1 m/s) restituisca praticamente il risultato della relatività galileiana, cioè la somma delle singole velocità dà come risultato il triplo della velocità di A.
Sarà giusto? Mah.....
Impegnato com'ero nei miei calcoli non mi sono accorto che Paolo aveva appena scritto le stesse cose (o quasi).
Vabbè, tutto torna e quindi son contento (sarà contento anche il prof. Zappalà che in 2, per ora, si sono cimentati).
cari Paolo e Guido,
sembrerebbe -forse- una sciocchezza leggere dei commenti con la soluzione, quando essa è già presente nel testo (volendo leggerla)... e, invece, è un segno meraviglioso! Questo dimostra che ci sono ancora persone che credono nell'onestà, che si cimentano e solo dopo vanno a controllare, qualsiasi sia il risultato. Che dirvi... COMPLIMENTI e GRAZIE... voi avete capito il vero spirito del Circolo e spero che i prossimi quiz non.quiz vi stimolino ancora di più e vi facciano considerare la RR una vera amica.
Per me la cosa più bella è che mi sto divertendo. Conoscere vagamente i principi generali (peraltro in modo molto approssimativo, nel mio caso, non essendo uno specialista della materia) è molto diverso dall'approfondire provando ad applicarsi a risolvere problemi e quesiti, anche se semplici. Tra riflessioni, calcoli, tentativi, errori e nuovi tentativi ci si avvicina a comprendere davvero la sostanza che sta dietro a tante frasi usate (e spesso abusate) nei testi divulgativi. Alcuni argomenti rimarranno sicuramente per me troppo difficili da capire ma qualche passo avanti lo sto facendo, l'orizzonte mi si amplia e questo è fonte d'entusiasmo. Un blog davvero utile, per quanto mi riguarda.
Andando a ruota libera si potrebbe fare il seguente ragionamento: l'esercizio in fin dei conti propone una specie di iterazione dello stesso procedimento (all'inizio considero un primo sistema di riferimento in moto rispetto a quello in quiete (modulo e capsula rispetto alla Terra) poi aggiungo un ulteriore sistema di riferimento in moto a sua volta rispetto alla Terra (astronave, capsula e poi modulo) e così via, tutti con la stessa V uno rispetto all'altro. E' come se stessi facendo delle iterazioni successive inscatolando un sistema di riferimento nell'altro. A qs punto posso chiedermi quanto "pesa" la composizione relativistica delle velocità ad ogni iterazione rispetto al sistema in quiete (Terra). Cioè calcolo nel caso del sistema astronave+capsula la differenza tra la Vtot secondo Galileo (sommo VA e VB cioè 2VA) e Vtot secondo Einstein. Dovrebbe uscire un valore Δ1 pari a 2VA(ß^2/1+ ß^2) con ß=VA/c.
Poi calcolo nel caso del sistema astronave+capsula+modulo la differenza tra Vtot secondo Galileo (sommo VA, VB e VC cioè 3VA) e Vtot secondo Einstein, usando ora la formula trovata alla fine dell'esercizio. Dovrebbe uscire un valore Δ2 pari a 8VAß^2/1+ 3ß^2.
Confrontando le due quantità Δ1 e Δ2 (per es. facendo la differenza tra la seconda e la prima) mi sembra che risulti Δ2>Δ1. Cioè procedendo con le iterazioni la composizione relativistica delle velocità "pesa" sempre più. Rispetto al sistema in quiete (Terra) la composizione einsteniana delle velocità si mangia una fetta sempre maggiore della velocità totale rispetto a quanto avrebbe pensato Galileo. Continuando nelle iterazioni l'incremento della velocità rispetto al sistema in quiete (Terra) appare via via minore anche se continuo ad aggiungere sistemi con velocità sempre uguale l'uno rispetto all'altro.
E' giusto il ragionamento?
Scusate lo sproloquio e consideratelo solo un mio esercizio mentale.
caro Guido,
il tuo ragionamento è corretto! In pratica dice che l'andamento della velocità relativistica tende asintoticamente al valore c, mentre quella galileiana può andare all' infinito... Basterebbe usare un diagramma velocità-tempo. Nel caso di Galileo avresti una retta, nel caso di Einstein una curva che comincia in modo analogo ma che poi tende a una retta orizzontale che è la velocità della luce. O diagrammi simili...
La serie continua, comunque... e avanti senza paura!!!!
La formula generale per n oggetti che si distaccano l'un l'altro con velocità è:
è:
Se n = 100 e la velocità di distacco fosse il 3% della velocità della luce ( 9000 km/sec) si raggiungerebbe facilmente la velocità della luce. Fattibile?
direi proprio di no..., caro Leandro, la velocità della luce è raggiungibile solo all'infinito... (asintoto). Se si raggiungesse si potrebbe anche superare aumentando il numero di capsule......
Non ho controllato la formula... domani lo farò
Non vorrei sbagliare, Leandro, ma il fattore che trovi tu è sempre minore di 1...
ß < 1 e quindi sia A = 1+ß che B = 1-ß sono quantità positive e A > B
Ne segue che il numeratore è sempre minore del denominatore e il fattore che calcoli è sempre minore di 1. Per cui c non si raggiunge mai a meno di porre ß = 1
((1 + 1)100 / 2 100 = 1
Si, intendevo velocità prossima a c , però sfruttando tanti piccoli incrementi di fattibilità tecnica. Dovrei fare un calcolo dell'energia totale necessaria, considerando anche le masse.
scusa Leandro... avevo interpretato male il tuo "raggiunge c".
Mettiamola così...
Se valesse Galileo le cose sarebbero ben più facili. Dopo 33 capsule arriveremmo alla velocità della luce e, soprattutto, dovremmo sempre impartire la stessa accelerazione alla capsula che viene lanciata.
Con Einstein le cose si complicano e si può anche usare la dinamica relativistica per capire che ad ogni nuovo lancio è cambiata la quantità di moto (o se preferisci la massa relativistica). Qualsiasi nuova capsula ha bisogno di un'energia sempre maggiore fino a diventare quasi infinita per v prossima a c. Passando alla RG possiamo dire che l'accelerazione necessaria aumenta sempre di più e si ottiene un incremento sempre più piccolo della velocità
Tuttavia, sono molto contento che un banale esercizio di RR abbia dato spunto per un discorso ben più ampio e ti ringrazio per i nuovi stimoli che proponi. Ovviamente si può sempre provare, ma vedrai che non faresti molta strada...
Abbiamo bisogno di persone che pensano e riflettono come te...