Categorie: Relatività
Tags: avventura spaziale gemelli Minkowski Minkowski per tutti nuovo paradosso relatività speciale
Scritto da: Vincenzo Zappalà
Commenti:23
NEW: Minkowski per tutti. 3: I gemelli sono proprio... paradossali! *** (con risposta nascosta)
Questo quiz-non quiz fa parte della serie "Minkowski per tutti". La soluzione è inserita in questo stesso articolo, ma sarebbe più interessante provare, prima di leggerla, a darla nei commenti, anche solo per esprimere le eventuali difficoltà incontrate.
Ho dovuto costruire una storia piuttosto rocambolesca per dare un risvolto pratico a un altro paradosso dei gemelli. Poverini... tutto ciò che succede a loro è sempre paradossale! Un piccolo strappo alla nuova regola: questa volta la soluzione sarà data tra pochi giorni...
Due esperti astronauti e ingegneri spaziali di altissima qualità decidono che sulla Terra "fa ormai troppo caldo" e decidono di abbandonarla per sempre, alla ricerca di un mondo migliore. Anzi, non credendo molto nella razza umana o aliena che sia, decidono di costruirsi una supernave, la cui forma sembra proprio quella di uno spaghetto rigido e cavo (un bucatino o -meglio- un bucatone?), lungo decine di chilometri, al cui interno si sono ricreate le migliori condizioni per una vita serena: foreste, laghi, montagne in miniatura, campi da sci, ecc., ecc. Non chiedetemi come sia possibile, ma con la tecnologia psicostruttiva del XXXII secolo, tutto si può fare (o quasi... dato che il riscaldamento globale continua imperterrito a mietere vittime virtuali). Basta pensare a un qualcosa di tecnologico, relativamente semplice, e le schiere di micro-robot virtuali ultra specializzati la costruiscono in men che non si dica. In realtà, proprio i due astronaut avevano messo a punto la tecnologia del pensiero...
Senza entrare troppo nei particolari tecnici, finalmente, i due amici decidono di partire insieme alle loro famiglie. Per avere una certa privacy, i due nuclei familiari si sistemano ai due estremi opposti della lunghissima nave, in due stupendi appartamenti sferici. Uno schema dell'astronave è riportata in Fig. 1.
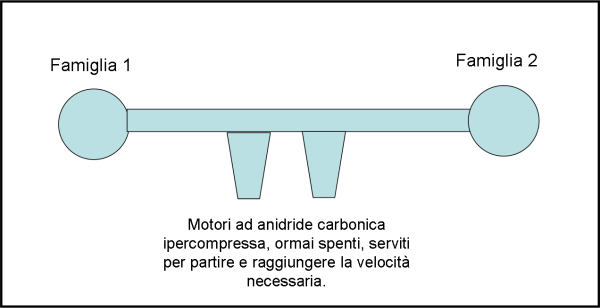
Il tempo passa e l'astronave si è fermata, ancorandosi a un pianeta (tenuto a debita distanza) privo di vita (non si sa mai). I due astronauti e le loro mogli decidono di dare un senso etico alla loro impresa che li sta soddisfacendo pienamente e decidono di far nascere un nuovo figlio, un vero figlio del futuro. Con facili preparativi che non sto a raccontarvi per la privacy, riescono a sincronizzare al miliardesimo di miliardesimo di secondo le due nascite. In poche parole, due perfetti gemelli nati da madri diverse. Un mondo nuovo, che deve anche avere un tempo nuovo scandito da un unico orologio posto al centro dell'astronave. Tutti gli altri vengono distrutti e Il nuovo tempo ZERO è quello della nascita dei gemelli!
Tutto sembra filare perfettamente liscio e i gemelli crescono spensierati. Ma ecco, un brutto giorno, giungere un asteroide probabilmente un po' invidioso (o magari inviato da qualche maligno terrestre?) che colpisce l'astronave proprio nella parte centrale, dove sono sistemati i due motori a CO2. Una tragedia che lascia miracolosamente salvi i due nuclei familiari, tenuti ormai insieme solo da una sottile asta molto rigida, che non permette, però, nessun contatto tra di loro. In pratica, due sfere lussuose, abbandonate nello spazio e tenute alla stessa distanza da un "filo". Un sistema in quiete veramente poco ... tranquillo. La situazione è mostrata in Fig. 2.
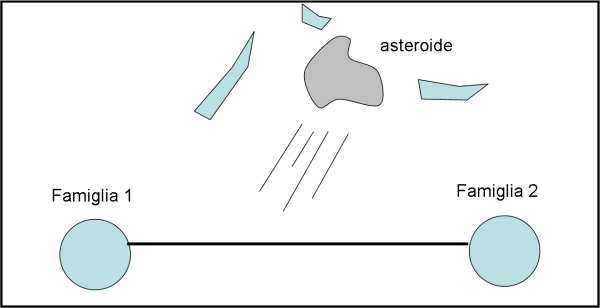
Forse proprio colui che aveva ordito il sabotaggio, pentitosi, o qualche nave pirata di passaggio si accorge del dramma e corre ai ripari informando la Terra. Viene immediatamente costruita una nave "acchiappafarfalle" (così chiamata in gergo) capace di recuperare dei naufraghi "al volo" attraverso due speciali reti (da cui il nome) poste ai due estremi del velivolo di soccorso. In questo caso deve recuperare istantaneamente i due moduli abitativi e i loro abitanti. Un'operazione che deve essere fatta con precisione millimetrica e con una astronave lunga il giusto. Qualcosa come quella mostrata in Fig. 3.
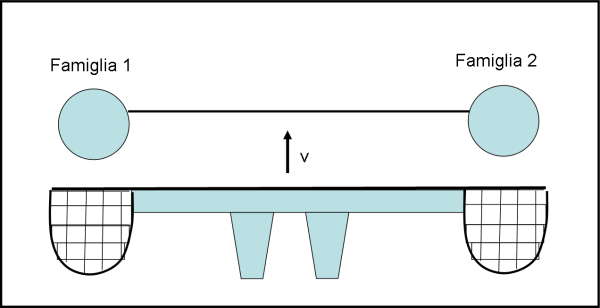
Un ciliegina sulla "torta"... Chi ha costruito la nave di soccorso è un amico carissimo dei due astronauti salvati al volo e ha costruito l'acchiappa farfalle esattamente come l'astronave originale. Con poche azioni psicostruttive la situazione torna identica a quella originale di Fig. 1.
Tuttavia, questa volta le due famiglie decidono di non fermarsi più e vagare per sempre nello spazio. La prima cosa che fanno è comunque correre una verso l'altra e abbracciarsi. Tutto bene? Vengono subito fatte le visite del caso con strumentazione medica d'avanguardia. Qualcosa, però, non va proprio per il verso giusto e si nota soprattutto nei due gemelli. Sembra proprio che siano stati colpiti da un "nuovo" paradosso. I genitori ci riflettono sopra e poi capiscono il motivo dell'apparente disfunzione (estremamente reale, però). Anzi, usano questa informazione per stabilire con precisione la velocità con cui stanno viaggiando.
Domande
1) Qual è la stranezza trovata nei due gemelli?
2) Qual è la formuletta (semplicissima) che permette di determinare la velocità della nuova astronave?
Le risposte sono decisamente facili e alla portata di moltissimi lettori... anche se necessitano di una certa dose di riflessione. Questa volta, perciò, faccio un piccolo strappo alla nuova regola e inserirò la risposta tra qualche giorno... Vale la pena meditarci sopra e costruire avventure anche più fantasiose e credibili della mia...
Forza, amici vicini e lontani, maghi e maghetti vari, principianti ed esperti, date le risposte e scrivete la vostra storia. Sono sempre più convinto convinto che entrare dentro alle bizzarrie dello spaziotempo sia un esercizio indispensabile, dopo più di cent'anni di vita della relatività einsteniana.
PS: ho inserito tre asterischi, ma, in realtà, riflettendoci un poco, potrebbero essere solamente due...
Questo articolo fa parte della serie MINKOWSKI PER TUTTI






23 commenti
Forza ragazzi... buttatevi che poi potremo anche finire su Andromeda... con un paradosso "filosofico"...
Ma un riposino ogni tanto ...no ? Io su Andromeda non ci torno.
Proporrei di chiamare con la lettera D la distanza tra le due sfere (decine di chilometri) corrispondente alla lunghezza del corridoio che le collega. Il valore di D determina l'entità della stranezza osservata ( se D fosse nullo, le due sfere coinciderebbero e non ci sarebbe niente di strano da osservare)
fin qui ci siamo... ma non solo la distanza...
ma non solo la distanza...
Ma come? tutte quelle belle serate a bere bicchieroni di Galoxhyar nelle taverne di Pungor IV ?
A Pungor IV , quella sera, mi sono giocato a dadi il mio Millennium Falcon e tutte le matite colorate della Caran D'Ache. Ho dovuto tornare a casa con l'Astro-stop e da allora non faccio più grafici a colori.
Niente grafici e niente formulette... Comunque, la butto lì, visto che tutti sono intenti a pensare....(spero).
Se l'astronave fosse ferma, le due famiglie giungerebbero al centro del corridoio (origine) senza alcun sfasamento temporale, i neonati avrebbero la medesima età e si troverebbero esattamente nello stesso stadio di sviluppo.
Viceversa, dato che l'astronave si muove a velocità v, gli assi di riferimento spazio e tempo ruotano, avvicinandosi alla bisettrice ( Minkowski) e i luoghi di nascita, che ad astronave ferma avevano le stesse coordinate temporali, vengono visti, nel nuovo sistema di riferimento, con valori di coordinate temporali diversi tra loro.
Per un gemello la coordinata temporale apparirà diminuita e per l'altro aumentata. Tra i due si crea quindi un gap temporale "delta t" che produce la "stranezza" osservata. Questa stranezza, potrebbe essere legata ad un diverso stadio di sviluppo, come la crescita di capelli, o denti, che anticipa per uno dei due rispetto all'altro. L'entità di questa manifestazione è legata al valore del delta t che la produce, che è proporzionale alla distanza D che separa i due luoghi di nascita e a beta ( = v/c), ossia alla velocità del movimento, rapportata alla velocità della luce.
Se è possibile quantificare lo sfasamento temporale "delta t", essendo nota la lunghezza del corridoio D, allora è possibile ricavare la velocità "v" del movimento .
non dovevo lasciarti solo quella notte!!! Tu e i tuoi giochi d'azzardo... e volevi convincer anche me con il tuo programmino sicuro... Pfui...
Caro Enzo, non ho ancora letto la soluzione e solo ora ho avuto il tempo per provare a rispondere.
Tu dici che l’astronave è ancorata ad un pianeta, per cui si può considerare come appartenente allo stesso sistema della Terra (è pressoché ferma rispetto alla Terra).
La nascita dei due gemelli avviene quando l’astronave è ancorata la pianeta, per cui avviene nel medesimo tempo per l’astronave e per la Terra (dato che in questa fase appartengono allo stesso sistema di riferimento).
Pertanto il tempo per i gemelli scorre allo stesso modo, finché l’astronave rimane ancorata al pianeta e nel sistema di riferimento terrestre lo stesso tempo (linea di simultaneità) è indicato da linee parallele all’asse x.
Tralasciamo cosa succede dopo l’impatto con l’asteroide, considerando semplicemente che l’astronave non è più in grado di viaggiare a causa della perdita dei motori e che la distanza tra le due famiglie rimane la stessa (qualche decina di chilometri).
L’informazione che l’astronave ha perso i motori impiegherà comunque un certo tempo per giungere a Terra (il tempo necessario alla luce per percorrere la distanza tra astronave e Terra).
Quando arriva l’astronave di soccorso, questa è costretta a “fermarsi”, per agganciare l’astronave in avaria.
Trascurando il tempo necessario per accelerare, quando l’astronave accende i motori e raggiunge una certa velocità di crociera le linee di simultaneità per il sistema astronave non sono più parallele all’asse x, ma diventano parallele all’asse x’ (inclinato rispetto all’asse x dello stesso angolo tra l’asse t’ e l’asse t).
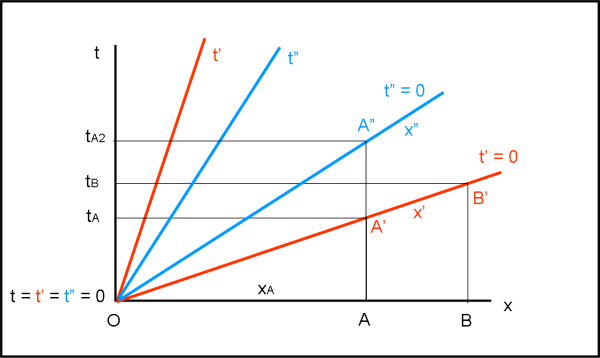
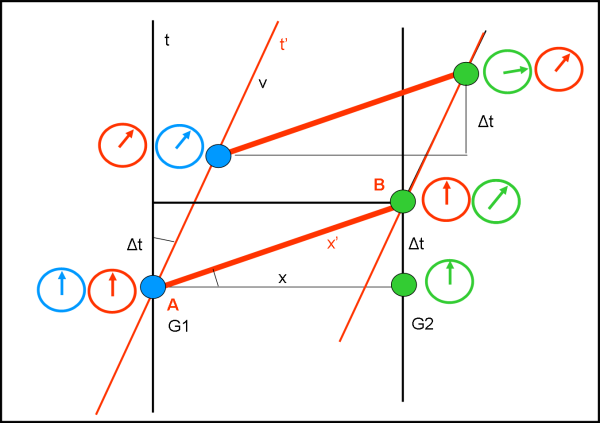
Dopo il salvataggio ogni sistema ha le sue linee di simultaneità (quelle dove gli orologi di quel sistema misurano lo stesso tempo), nere per la Terra e l'astronave prima del recupero (linee parallele all'asse x) e rosse per l'astronave in movimento dopo il recupero e l'avvio dei motori (linee parallele all'asse x').
Tale situazione è mostrata nella figura sottostante.
Come è facile notare, prima del salvataggio, le due famiglie F1 e F2, si muovono con la medesima rapidità lungo gli assi del tempo t, paralleli all’asse del tempo terrestre.
Pertanto, prima del salvataggio, i gemelli nati sull’astronave quando era ancorata al pianeta, hanno sicuramente la medesima età, come indica la linea di simultaneità al tempo t F1-2, del sistema Terra e astronave “ferma”.
Dopo il salvataggio e l’avvio dei motori (considerando trascurabile il tempo per raggiungere la velocità di crociera), per le due famiglie cambia completamente la linee di simultaneità, per cui gli eventi simultanei per il sistema Terra non lo sono per il sistema astronave “in movimento” e viceversa.
Per il sistema Terra e l'astronave “ferma”, prima del recupero dell'astronave in avaria il gemello F1 ha la stessa età del gemello F2 (linea di simultaneità t 1-2), dopo il recupero il gemello F2 ha un'età maggiore rispetto al gemello F1 (tF'2 > tF1-2).
Per il sistema astronave “in movimento”, dopo il recupero dell'astronave e l'avvio dei motori (senza considerare il tempo di accelerazione) la linea di simultaneità (rossa) che congiunge le due famiglie cambia completamente (t'F'1-2).
Ciò significa che quando le due famiglie si muovono per incontrarsi, se il gemello della famiglia 1 si trova all’incirca nella stessa posizione spaziotemporale dell’astronave ferma (F1 = F'1), il gemello della seconda famiglia non è più nella stessa posizione di prima (F2 ≠ F'2) e si è mosso lungo una linea parallela all’asse t’.
E' del tutto evidente che quando le due famiglie si incontrano notano a mio avviso non una ma due cose strane.
Tali stranezze sono il risultato del cambiamento del sistema di riferimento dopo l'avvio dei motori dell'astronave (o meglio dopo che l'astronave raggiunge la sua costante velocità di crociera).
La prima cosa “strana” è che il gemello della seconda famiglia (F2) è leggermente più vecchio di quello della prima famiglia (F1).
E’ un po’ come se con l’astronave in movimento, la famiglia F1 incontrasse la famiglia F2 del “futuro”, o perlomeno del futuro per il sistema Terra e per il sistema astronave ancorata al pianeta (astronave ferma)....
D’altronde con l’avvio dei motori, le due famiglie si muovono lungo gli assi del tempo t’ e non più lungo gli assi del tempo t, per cui se per l’astronave F’1 e F’2 sono eventi simultanei, per la Terra non lo sono affatto.
Quindi quando le due famiglie si incontrano, notano che il gemello F2 è leggermente più vecchio del gemello F1… è un po’ come se il gemello F2 abbia subito istantaneamente un salto temporale notevolmente maggiore rispetto al gemello F1 (tF’2 > tF1-2).
Ovviamente tutto ciò non avviene proprio istantaneamente, in realtà dall’avvio dei motori al raggiungimento della velocità di crociera passa un certo intervallo di tempo (è un po’ come se il sistema di riferimento mutasse continuamente fino a raggiungere quello finale della velocità di crociera), per cui il salto temporale non è istantaneo ma un pochino più diluito di quanto mostrato in figura.
Ciò non toglie che gli effetti di questo cambio di sistema di riferimento si fanno sentire eccome, tanto che il gemello F2 è leggermente più anziano del gemello F1.
La seconda stranezza è che il percorso che separa le due famiglie (il lungo corridoio della parte centrale dell'astronave), sembra più lungo rispetto a prima.
Innanzitutto vorrei fare una piccola premessa.
Per misurare una lunghezza o una distanza, ovviamente devo farlo nello stesso tempo…
Pertanto il sistema Terra misura le distanze lungo l’asse x o sue linee parallele (ossia quando tutti i suoi orologi sincronizzati segnano lo stesso tempo t), mentre il sistema astronave in movimento misura le distanze lungo il suo asse x’ o sue linee parallele (quando tutti i suoi orologi sincronizzati segnano lo stesso tempo t’).
Le due famiglie, con l’astronave in movimento, si muovono solo lungo gli assi del tempo t’ e la loro distanza per il sistema astronave in movimento è rappresenta dal segmento rosso F’1-F’2 (al tempo t’F’1-2).
Il sistema Terra può misurare la distanza tra le due famiglie con l’astronave in movimento solo usando linee parallele all’asse x, ossia quando queste tagliano gli assi del tempo t’ lungo cui si muovono le estremità (F’1 e F’2)dell’astronave in movimento.
Quindi, anche tenendo conto che il sistema astronave in movimento ha le sue unità di misura (non fatevi ingannare da segmenti che in alcuni casi possono apparire più lunghi, poiché bisogna sempre considerare le rispettive unità di misura), la distanza tra le due famiglie F’1 e F’2 misurata dal sistema Terra appare contratta ed è uguale al segmento F1-F2 (ossia alla distanza d tra le due famiglie con l’astronave ferma).
Quindi, quando le due famiglie si ricongiungono, si accorgono anche che il corridoio è più lungo rispetto a quando l’astronave era ferma.
Misurando il corridoio dell’astronave in movimento (segmento rosso parallelo all’asse x’ che unisce F’1 a F’2), con le specifiche unità di misura di quel sistema (X’(F’2) - X’(F’1)) e confrontandolo con le misure conosciute dell’astronave ferma (X (F2) - X(F1)), ossia quelle usate anche per costruire l’astronave di soccorso è possibile ricavare la velocità di crociera.
Infatti basta applicare la nota formula sulla contrazione delle lunghezze:
(X’(F’2) - X’(F’1)) = (X (F2) - X(F1)) 1/√(1-v²/c²)
Per semplicità chiamiamo d0 la distanza tra le due famiglie misurata dal sistema astronave in movimento (X’(F’2) - X’(F’1)) e d la distanza misurata dal sistema Terra (X (F2) - X(F1))
d0 = d/√(1-v²/c²)
√(1-v²/c²) = d/ d0
1-v²/c² = d²/d0²
1- d²/d0² = v²/c²
(d0²- d²)/d0² = v²/c²
(d0²- d²) c²/d0² = v²
v = √(d0²- d²) c²/d0²
v = (c/d0) √(d0²- d²)
Spero di non aver toppato, anche se ho presente che il quiz parlava di una sola stranezza e di ricavare la velocità usando la differenza di età tra i due gemelli e non la lunghezza del corridoio… ma a volte seguire strade diverse può essere interessante… o può anche aumentare la possibilità di sbagliare… ma è proprio sbagliando e ragionando sugli errori che si impara…
Paolo
caro Paolo,
OK per la prima parte... ma non sono molto d'accordo con la seconda (sempre che l'abbia capita bene...). L'astronave di soccorso vista dalla terra ha una lunghezza contratta rispetto a quella che era la distanza tra le famiglie sulla vecchia astronave. Poco c'importa cosa vede adesso la Terra (la distanza originaria tra le famiglie era ben maggiore di quanto disegnato da te)... La figura che ho fatto io è un po' diversa e la formula la ricavo in altro modo... considerando solo la distanza originaria tra le due famiglie. Secondo me la lunghezza propria è diminuita rispetto a quella originaria...
Potrei anche sbagliare... ovviamente...
Caro Enzo, non so io ho fatto questo ragionamento.
Facciamo finta che l’asse x passi per F1 e F2 (segmento nero) e che l’origine degli assi sia in F1.
Guardando la figura, ammettiamo che il segmento rosso F’1 – F’2 sia lungo secondo il sistema di riferimento S’ (quello dell’astronave) esattamente 1 secondo luce.
Tracciando da F’2 la parallela all’asse t’, dovrei incrociare l’asse x (passante per F1 e F2) esattamente ad 1/γ (se la velocità è di 0,8 c esattamente a 0,6 secondi luce).
Per questo ho ritenuto che il segmento nero F1-F2 sia la misura contratta vista dal sistema in quiete (terra) del segmento rosso F’1-F’2.
Se provo a verificare le misure con un righello i conti tornano e trova la velocità corretta
Dove sbaglio?
Paolo
caro Paolo,
non mi trovo con la tua figura... Dov'è la striscia di Universo della nave bloccata sul pianeta? Questa deve essere una striscia con x1 e x2 costanti. I due gemelli devono essere catturati istantaneamente nel sistema della nave di soccorso, ma devono esser entrambi sulla striscia di universo della nave rotta. Questo non lo vedo nella tua figura, dato che F2 si è spostato misteriosamente in F2', mentre prima di essere raccolto deve stare lungo la perpendicolare a x di F2. Sia F1 che F2 devono essere ancora sulla loro striscia di universo nel momento in cui vengono prelevati dall'astronave di soccorso. F2' non ha alcun significato... chi sarebbe ?
Caro Enzo forse ho capito dove sta il problema.
Io ho inteso che l’astronave di soccorso, arriva, si ferma, ingabbia quella in avaria (figura 3) comprese le due famiglie e poi parte a velocità relativistica.
Quindi per me quando l’astronave di soccorso si ferma il suo sistema di riferimento è lo stesso della Terra e di quella in avaria (con la linea di simultaneità nera parallela all’asse x) ed in quel frangente carica F1 e F2.
Una volta che l’astronave riparte e raggiunge la velocità di crociera F’2 è l’evento simultaneo con F’1.
Se non ho capito male, invece nel quiz l’astronave di soccorso già viaggia alla sua velocità di crociera quando carica le due famiglie.
Il mio dubbio era che così facendo non coincidono le lunghezze delle due astronavi, ossia non si può impacchettate l’astronave in avaria come nella figura 3.
In pratica io ho considerato il quiz come un’astronave che da ferma parte a velocità relativistica, cambiando così le sue linee di simultaneità (anche se ora pensandoci bene in questo caso ho dei dubbi che i due gemelli risultino con età diverse… la loro età non coincide se viste dal sistema Terra) …
Forse l’errore è questo !
Paolo
penso proprio di sì...
Infatti, scrivo:
"capace di recuperare dei naufraghi "al volo" attraverso due speciali reti (da cui il nome) poste ai due estremi del velivolo di soccorso. In questo caso deve recuperare istantaneamente i due moduli abitativi e i loro abitanti. Un'operazione che deve essere fatta con precisione millimetrica e con una astronave lunga il giusto"
La Fig. 3 non è un diagramma di Minkowski e forse può ingannare... La nave deve avere delle dimensioni tali che la sua lunghezza sia più corta nel sistema della Terra rispetto alla distanza tra le due capsule (quello che tiene unite assieme viene tranquillamente eliminato, ossia la nave originaria può essere incapsulata, dato che le due sfere sono libere anche se ancora trattenute a malapena nello stesso sistema terrestre). In pratica è la Fig. 38 dell'articolone su Minkowski.
Per trovare dt in funzione di lunghezza originaria e velocità basta usare una delle equazioni della trasformazioni di Lorentz, assumendo il primo gemello (a sinistra) come origine degli assi di entrambi i sistemi...
Può darsi che non sia riuscito a spiegarmi bene... ma dovevo mantenere i gemelli nello stesso sistema prima di essere prelevati simultaneamente da un oggetto in volo...
caro Mau...
tu a quale figura avevi pensato? Avevo tratto in inganno anche te oppure sei in linea con la mia spiegazione... Non vorrei proprio aver prodotto un non quiz spiegato male...
Stai tranquillo che non ti mando su Andromeda, ma te la faccio solo guardare al telescopio....
Caro Enzo sono io che ho frainteso il quiz ed ho commesso un errore nel cercare di fornire la soluzione… ma come ho sempre sostenuto sbagliare non è un problema, l’importante è analizzare gli errori e superarli….
Come d’altronde è appena accaduto…
Paolo
Caro Paolino,
Sapessi quanti errori ho fatto io... e ne farò ancora... per cui statemi dietro e fermatemi quando ve ne accorgete. Per non commettere errori bisognerebbe non cercare di migliorarsi, ma questo sarebbe un errore ben più grave!
Essendo più superficiale di Paolo in materia di RR, mi sono lasciato guidare da quella frase "recuperare al volo" e il discorso conseguente viene a coincidere con le tue spiegazioni. A volte basta pensare meno, anche se chi pensa di più, come Paolino, impara di più.
Se i motori , invece che venire distrutti fossero stati semplicemente accesi, portando istantaneamente il sistema alla velocità v , non sarebbe successa la stessa cosa?
direi di no,dato che entrambi passerebbero immediatamente nel nuovo sistema senza nessun tempo dt di attesa. Tuttavia, pensare a una velocità costante immediata sarebbe dura....
Giusto così per fare un piccolo test.
Ammettiamo di voler passare da fermi ad una velocità di 0,8 c (ossia circa 240 000 000 mt/sec).
Passare in un secondo a tale velocità ridurrebbe gli sventurati astronauti a dei frullati a causa dell’accelerazione.
Basta ricordare che:
a = (V1-V0)/(t1 – t0) = (240 000 000 – 0)/(1 - 0) = 240 000 000 mt/sec²
Considerato che l’accelerazione di gravità terrestre è pari a 10 mt/ sec², significa che gli astronauti dovrebbero sopportare un’accelerazione 24 milioni di volte maggiore della gravità terrestre.
Poveri astronauti…
Ammettiamo invece di limitarsi ad un’accelerazione costante pari a 5g ossia 5 volte l’accelerazione di gravità terrestre al suolo, per cui:
a = 50 mt/sec²
Quanto tempo ci vorrebbe (misurato dal sistema terricolo) per raggiungere la velocità di crociera di 0,8c ?
a = (V1-V0)/(t1 – t0)
(t1 – t0) = (V1-V0)/a
(t1 – t0) = (240 000 000 -0)/50 = 4 800 000 secondi (quasi 5 milioni di secondi)
Espressi in ore:
4 800 0000/3600 = 1333,33 ore
Espressi in giorni:
1333,33 /24 = 55,55 giorni (poco più di 55 giorni)
Spero che il test ed il ragionamento siano corretti…
Paolo
In realtà, Paolo, perché mai dovrebbero sentire un'accelerazione? Tu hai posto come tempo un secondo, ma nel nostro caso è molto di meno: è un passaggio istantaneo da 0 a 0.8 c... sempre teoricamente... e senza pensare a quantità di moto... sarebbe come se una mosca immobile entrasse dentro un aereo. Lei starebbe sempre ferma fino a sbattere contro la parte posteriore... e , schiacciata, inizierebbe subito a muoversi a 0.8 c. O ho capito male il problema...?
Ah... ma forse tu ti riferivi al caso sollevato da Mau... chiedo perdono!
Giuro che non prenderò mai più "al volo" due famiglie di astronauti. Vederli ridotti a polpettone informe....
A meno che .... Non provengano da un pianeta che ha proprio quel valore di gravità, a cui sarebbero abituati da sempre, una specie di super buco nero. Qualcuno sarà pur abitato...
Salve, scusate ma a me la soluzione non sembra giusta.
"Maggiore è la distanza tra due eventi simultanei in un sistema in quiete e maggiore è lo sfasamento del tempo rispetto a un sistema in moto con una certa velocità v1."
Giusto, però solo se la distanza di cui si parla è nella stessa direzione della velocità v1, non è forse vero?
In questo caso, la distanza tra i due gemelli ha la componente parallela a v1 pari a zero (come si capisce dalla freccia e anche dalla posizione dei motori in Fig 3), quindi non mi aspetto nessuno sfasamento di tempo (né contrazione della distanza D).
O si tratta forse di un errore nella figura?
Caro Dario,
la Fig. 3 fa solo vedere la situazione nello spazio a due dimensioni. Tutt'altra cosa è passare allo spaziotempo di Minkowski. Per come si costruiscono le cose, se qualcosa si muove rispetto a qualcos'altro, v1 non può essere parallela a una linea che è ferma. La rappresentazione la vedi bene nella Fig. 5. B viene raccolto prima di A.
Il diagramma di Minkowski che usiamo è a una sola dimensione spaziale, quella dell'asse x.