Categorie: Relatività
Tags: eventi Minkowski Minkowski per tutti ordine cronologico quiz non quiz relatività speciale simultaneità relativa sistemi di riferimento
Scritto da: Vincenzo Zappalà
Commenti:12
Minkowski per tutti. 4 : un treno in galleria **
Questo quiz-non quiz fa parte della serie "Minkowski per tutti". La soluzione è inserita in questo stesso articolo, ma sarebbe più interessante provare, prima di leggerla, a darla nei commenti, anche solo per esprimere le eventuali difficoltà incontrate.
Questo esercizio è veramente un classico per la RR e potrebbe sembrare un paradosso solo a chi non l’ha compresa appieno. Ricordiamo che i fenomeni fisici devono essere uguali in ogni sistema di riferimento, ma non possiamo pretendere che si mantenga la simultaneità dei vari eventi. Un esercizio veramente facile alla portata di molti...
Abbiamo due “personaggi” nella nostra avventura ferroviaria: un treno e una galleria. Per quello che vogliamo mostrare in questo quiz non-quiz c’interessa poco sapere se è più lungo il treno o la galleria (si potrebbe farlo utilizzando l’iperbole di calibrazione o le formule relative), dato che vogliamo limitarci alla successione di certi eventi dello stesso fenomeno “il treno entra ed esce da una galleria”.
Poniamo come sistema in quiete quello della galleria. Il sistema in moto ad alta velocità è invece il treno. Per rendere un po' più difficile e "personale" l'esercizio non disegniamo nessuna figura di partenza e lasciamo il compito ai lettori.
Ricordiamo solo che il sistema nero è quello in quiete ed è immediato disegnare la galleria come un segmento AB dove a sinistra c’è l’entrata e a destra l’uscita. La lunghezza della galleria è una lunghezza propria dato che viene misurata nello stesso istante del sistema in quiete.
Per non costringerci a utilizzare l’iperbole di calibrazione (ma lo faremo.., ah… se lo faremo!) nello stesso grafico disegniamo il sistema di riferimento rosso relativo al treno (t’, x’) e la sua lunghezza CD in questo sistema. La velocità che imprimiamo è importante per la risposta, così come la lunghezza del treno. Esso si dispone ovviamente lungo l’asse spaziale x’. La sua lunghezza è quella propria, dato che viene misurata nello stesso istante t’.
Ovviamente, la stessa lunghezza, misurata nel sistema della galleria, deve essere diversa (contrazione delle lunghezze...).
Si chiede:
a) Stabilire l’ordine cronologico dei seguenti eventi, nei due sistemi di riferimento (galleria e treno).
Evento 1 : entrata della testa del treno in galleria Ten; evento 2: uscita della testa del treno dalla galleria Tus; evento 3: entrata della coda del treno in galleria Cen; evento 4: uscita della coda del treno dalla galleria Cus
b) Nel sistema dell’osservatore O il treno sparisce completamente all’interno della galleria? Se sì, in quale intervallo di tempo Δt?
c) Nel sistema del treno, il treno rimane completamente all’interno della galleria? Se sì, in quale intervallo di tempo Δt’?
Ribadiamo che la risposta dipende molto dalla vostra scelta fatta sulla lunghezza propria della galleria, sulla velocità del treno e sulla lunghezza propria del treno. Potete anche variare queste impostazioni e notare se scaturiscono diverse soluzioni...
RISPOSTA
Chi vuole conoscere subito la risposta, non deve fare altro che schiacciare "mostra risposta" (invitiamo, però, chi conosce le basi della RR a provare, prima, da solo...)
Questo semplice esercizio permette di affrontare con sicurezza un celebre “paradosso-non paradosso” della RR, che abbiamo già trattato e che inseriremo tra questi problemi didattici (non andatelo a cercare...): quello dell’auto e del garage (magari anche con la porta chiusa…).
Questo articolo fa parte della serie MINKOWSKI PER TUTTI







12 commenti
Caro Enzo, provo a rispondere al quiz, sperando che altr@ provino a rispondere, senza leggere prima la soluzione (e nemmeno la mia possibile soluzione) come ho fatto anch'io.
Parto dalla prima domanda, avvertendo che la risposta dipende dalle lunghezze proprie e dalla velocità utilizzata.
La prima figura mostra una prima possibile soluzione, usando le diverse linee di simultaneità dei due sistemi (quello dove gli orologi sincronizzati di quel sistema segnano lo stesso tempo).
Ovviamente ogni sistema misura le sue distanze quando gli orologi sincronizzati segnano lo stesso tempo, quindi usando linee parallele all'asse x per il sistema galleria e parallele all'asse x' per il sistema treno.
Le due estremità della galleria si muovono solo lungo le due linee nere parallele all'asse del tempo t (questa è la linea di universo della galleria), mentre le due estremità del treno si muovono solo lungo le due linee rosse parallele all'asse del tempo t' (questa è la linea di universo del treno).
Ovviamente ciò che è simultaneo per un sistema non lo è per l'altro ed ognuno ha le proprie misure di spazio e tempo... solo la velocità della luce è identica per entrambi i sistemi di riferimento.
E' del tutto evidente che mentre per il sistema della galleria prima entra la coda del treno e poi esce la testa (tTu > tCe), per il sistema treno la coda del treno entra solo dopo che è uscita la testa del treno (t'Ce>t'Tu).
Quindi, mentre per il sistema galleria il treno rimane per un certo intervallo di tempo dentro la galleria, per il sistema treno non è così, ossia quando la coda del treno entra in galleria, la testa è già uscita da un po'.
La figura 2, prova a rispondere alle altre due domande.
Per il sistema galleria, quando la coda del treno entra in galleria (evento Ce), la testa del treno non ha ancora raggiunto l'uscita della galleria (evento Tu), ossia tTu > tCe.
Il sistema galleria misura la distanza su assi paralleli all'asse x , pertanto i due estremi del Treno (che si muovono lungo gli assi t) si trovano all'interno della galleria (Ce-T < L).
Il segmento Ce-T non è altro che la lunghezza contratta del treno vista dal sistema galleria, ossia Ce-T = L’/γ.
Ciò significa che al tempo tCe del sistema galleria, la testa del treno (T) si trovava ad una certa distanza dall'uscita della galleria (Δx).
Dato che la velocità del treno è conosciuta in rapporto a quella della luce (β = V/C), è ovvio che per percorrere tale distanza il treno impiega un certo intervallo di tempo (Δt).
Quindi considerato che Δx non è altro che la differenza tra la lunghezza propria della galleria e quella contratta del treno misurata dal sistema galleria, ossia:
Δx = L - L’/γ
e che tale distanza è anche uguale a:
Δx = β Δt
uguagliando le due equazioni, si ottiene:
L - L’/γ = β Δt
Δt = (L – L’/γ)/ β
Questo è l'intervallo di tempo in cui il treno rimane all'interno della galleria secondo il sistema galleria, ossia l'intervallo di tempo che scorre da quando la coda del treno entra in galleria (tCe) a quando la testa del treno esce dalla galleria(tTu).
Per il sistema treno, invece, quando la coda del treno entra in galleria (evento Ce), la testa del treno è già uscita dalla galleria (evento Tu), ossia t'Ce > t'Tu.
Infatti, la lunghezza propria del treno (L') risulta maggiore di quella contratta della galleria (L/γ) ossia :
L' > L/γ
segue
Cambiando le lunghezze di galleria e/o treno e/o la velocità, si possono ottenere anche altre risposte.
Il procedimento seguito è lo stesso di quelle precedentemente descritto, ma cambia la lunghezza della galleria.
Ora per entrambi i sistemi il treno rimane all'interno della galleria per un certo intervallo di tempo ed infatti l'ordine cronologico degli eventi è lo stesso per entrambi i sistemi di riferimento e nello specifico sia per il treno, sia per la galleria, quando la coda del treno entra in galleria (Ce), la testa non ha ancora raggiunto l'uscita (Tu):
tTu>tCe
t'Tu>t'Ce
Ovviamente l'intervallo di tempo non è lo stesso.
Per il sistema della galleria, prima era già stato ricavato l'intervallo di tempo (ovviamente ora cambia il valore della lunghezza propria L) della galleria, ossia:
Δt = (L – L’/γ)/ β
Per il sistema del treno, la velocità (espressa come β = V/C) non è altro che il rapporto tra Δx'/Δt', ossia
β = Δx'/ Δt'
e 'Δx' = β Δt'
Inoltre Δx' non è altro che la differenza tra la lunghezza contratta della galleria misurata dal sistema treno (L/γ) e quella propria del treno (L'), ossia:
Δx' = L/γ - L'
uguagliando le due equazioni, si ottiene:
L/γ -L' = β Δt'
Δt' = (L/γ - L')/ β
A mio avviso è inutile proseguire con altri esempi... come per esempio una galleria che per entrambi i sistemi è troppo corta rispetto alla lunghezza del treno, ossia dove per entrambi i sistemi quando la coda del treno entra in galleria la testa è già uscita dalla galleria...
Spero di non aver commesso errori.
Paolo
Paganini non ripete, ma la RR è diventato il pane di Paolo... (non controllo nemmeno i calcoli...). Forse sarebbe bene inserire il tutto nell'articolo... vediamo...
Gli altri non si spaventino... basta molto meno, una sola figura senza calcoli...
Buongiorno, ma come faccio ad inserire i disegni? Ho provato a salvarli come immagini ma quando tento di copiarli nel testo non vedo nulla.
Scusate la mia imperizia.
scusa Guido... è meglio che ri risponda Scherzy... lui è il mago tecnologico... io sono moooolto imbranato! Abbi pazienza...
Ciao Guido, anche se non sono papalscherzone.... per inserire un immagine, prima devi caricarla su qualche sito (io uso postimage, ma vanno bene anche altri), poi dalla barra degli strumenti clicca su inserisci/modifica immagine (l'icona assomiglia a quella con due montagne ed un punto sopra a destra) e copi il link diretto della tua immagine su "sorgente", clicchi Ok e dovrebbe comparire l'immagine nel tuo post.
Paolo
grazie Paolino... ormai hai una costante velocità relativistica !!!!
Ciao Guido, quando accedi a
https://postimage.org
Per caricare le tue immagini è preferibile che ti registri a quel sito (gratis) affinché le immagini restino disponibili anche in futuro.
Non registrandosi restano per un periodo limitato e poi non si vedono più nel tuo commento.
A motivo della mia scarsa dimestichezza con Minkowski seguo i suggerimenti del testo del quiz-non quiz, comincio quindi con il riportare il segmento CD (treno) sull’asse x’ del sistema di riferimento ad esso solidale (assi in rosso). Stabilisco una lunghezza di CD arbitraria. Allo stesso tempo ho implicitamente stabilito la velocità del treno, cioè del sistema di riferimento in moto rispetto a quello in quiete, la velocità di tale sistema (assi rossi) influisce sull’angolo di apertura tra l’asse t’ e x’: maggiore la velocità minore l’angolo tra gli assi, per v=c gli assi coincidono (angolo nullo). Poiché la lunghezza del segmento CD è una lunghezza propria occorre riportarla nel sistema di riferimento solidale con la galleria (sistema in quiete) tracciando la parallela all’asse t’ (tratteggio), ottengo così la lunghezza del treno contratta, segmento CDgal. Sull’asse x riporto ora il segmento AB che rappresenta la galleria, che scelgo di lunghezza arbitraria (lunghezza propria poichè è misurato nel proprio sistema di riferimento). Traccio ora le linee parallele all’asse del tempo t del sistema di riferimento in quiete. Le 2 linee verticali verdi rappresentano la galleria (ferma nel suo sistema di riferimento). Allo stesso modo traccio anche la linea rossa passante per D e parallela all’asse del tempo t’ (in rosso) del sistema di riferimento solidale col treno. L’asse T’ e la parallela ad esso rappresentano il treno (fermo nel proprio sistema di riferimento).
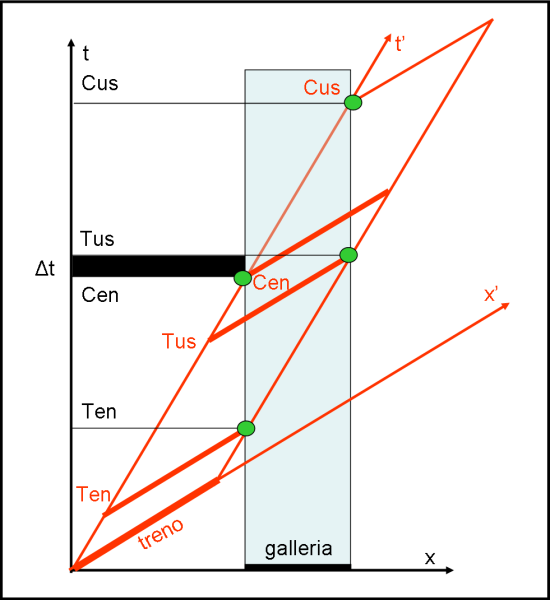
Nel sistema in quiete (assi t-x neri) posso quindi riportare il treno (segmento blu) in vari istanti, poiché si sposta la sua ascissa cambia e anche la sua ordinata. Tra queste posizioni scelgo gli istanti Ten in cui la testa del treno entra in galleria, Tus in cui la testa esce dalla galleria, Cen in cui entra la coda e Cus in cui la coda esce, contrassegnati dal pallino in blu, l’ordinata dei punti stabilisce così la mia sequenza nel sistema di riferimento in quiete:
Ten, Cen, Tus, Cus
Ora cambio sistema di riferimento e passo al sistema solidale con il treno, il segmento ora è quello nero con i pallini neri che contrassegnano gli stessi eventi di prima: testa che entra, coda che entra etc etc però i segmenti questa volta fanno ciò che faceva la galleria nel caso precedente, cioè non si spostano se non lungo l’asse t’ (il tempo proprio scorre mentre il treno sta fermo, la galleria si muove):
Poiché le linee di contemporaneità sono parallele all’asse x’ (nella figura sono nascoste dai segmenti neri che rappresentano il treno) la loro intersezione con l’asse t’ stabilisce gli istanti corrispondenti agli eventi di ingresso testa treno, uscita testa treno e così via.
La sequenza degli eventi non cambia rispetto all’altro sistema di riferimento: Ten, Cen, Tus, Cus.
Però si vede bene che mentre i 4 eventi sono circa equidistanti nel tempo nel sistema di riferimento in quiete (assi neri) i 4 medesimi eventi non sono più circa equidistanti nell’altro sistema (assi rossi, vedi intervallo C’en-T’us rispetto a T’en-C’en).
Se cambio la velocità del treno cambia l’inclinazione di t’ e x’ e cambiano le mutue posizioni dei pti neri, in particolare chiudendo la forbice degli assi x’-t’ (aumentando la velocità del treno) si arriva ad una condizione in cui gli istanti C’en e T’us coincidono nel sistema di riferimento rosso mentre si mantengono separati in quello nero. Stringendo ancor più la forbice l’istante T’us scavalca l’istante C’en e finisce per precederlo. In altri termini la galleria subisce una contrazione tale della lunghezza da diventare, nel sistema di riferimento rosso, più corta del treno.
Nel sistema di riferimento in quiete (galleria ferma) il treno è completamente contenuto nella galleria tra gli istanti Cen e Tus (vedi segmenti azzurri), nell’altro sistema di riferimento accade la stessa cosa ma per un intervallo di tempo minore (sempre paragonandolo alle rispettive unità di misura temporali). Le condizioni di velocità in cui C’en e T’us coincidono (caso poco sopra accennato) corrisponde all’unico istante in cui treno e galleria sono di pari lunghezza.
Le figure mi sono costate una quantità di tempo e fatica inaudite, la prossima volta allego una scansione di un disegno fatto a mano che faccio prima!
Molto bene Guido... ti ringrazio per la volontà di provare e per l'attenzione che hai messo nella descrizione. Ce ne fossero tanti come te... Se vuoi inserire un disegno, va bene lo stesso... anzi è ancora più istintivo...(però fatto bene, mi raccomando ). E' vero o no che prendendo dimestichezza con Minkowski molte cose acquistano un significato più profondo e generale, rendendo la RR una realtà ben comprensibile? Ed evitando gli errori che ancora si leggono su molte pagine del web...
). E' vero o no che prendendo dimestichezza con Minkowski molte cose acquistano un significato più profondo e generale, rendendo la RR una realtà ben comprensibile? Ed evitando gli errori che ancora si leggono su molte pagine del web... 
E' verissimo! W Minkowski! Già studiando cosa significa e come si rappresentano gli eventi su di esso si riesce a capire ma usandolo per fare gli esercizi si accende davvero la luce. Devo dire che è stato impegnativo l'inizio e ci ho messo un po' ma ragionandoci bene sopra e soprattutto ponendomi le domande giuste sono riuscito a inquadrare il suo uso. Fondamentale davvero perchè si "vedono" proprio gli eventi che si spostano nello spaziotempo al cambiare dei sistemi di riferimento.
grande Guido!!!!
