La nostra avventura “golfistica” rispecchia, con varianti solo apparenti, un "problema" noto per essere stato introdotto in un programma televisivo condotto da Maurice Halprin, noto con lo pseudonimo di Monty Hall. Il problema è anche noto come paradosso di Monty Hall, poiché la soluzione può apparire controintuitiva, ma in realtà non lo è affatto.

Noi abbiamo introdotto un secondo “giocatore”, ma, in realtà, niente abbiamo cambiato rispetto al problema classico che consiste in una semplice doppia richiesta da parte del conduttore a un singolo giocatore.

Questo il caso classico: vi sono tre porte. Una di queste nasconde una splendida automobile, mentre le altre due nascondono una capra. Il conduttore sa benissimo dove stanno le capre e l’automobile (questo fatto è importante). Viene chiesto al giocatore di scegliere una porta. In queste condizioni è ovvio che la probabilità che ha  di vincere l’automobile è 1/3.

A questo punto è anche chiaro che le altre due porte assieme abbiano una probabilità pari a 2/3 (due possibilità su 3). In poche parole, ogni porta ha 1/3 di probabilità. Per cui 2 porte hanno 1/3 + 1/3 = 2/3 di probabilità. Tuttavia, è anche ben noto che dietro a una di queste due deve esserci una capra.  E il conduttore non ha problemi ad aprire proprio quella porta.. Arriviamo così al punto chiave che può mettere in imbarazzo. La probabilità di 2/3 delle due porte rimane la stessa anche per l’ultima porta ancora chiusa, dato che era ovvio che ce ne fosse una con la capra. Averne lasciate due chiuse o averne aperta una, sicuramente con la capra, non cambia assolutamente la probabilità delle due porte rimaste che ormai si presentano come una sola. La probabilità resta 2/3 sia prima che dopo l’apertura della porta con la capra. L’ultima porta chiusa ha quindi conservato la probabilità 2/3.

A questo punto il conduttore chiede al giocatore se preferisce tenersi la porta scelta all’inizio o cambiarla con l’altra rimasta chiusa. Le loro probabilità sono rimaste quelle che erano all’inizio (1/3 contro 2/3) e cambiando porta il giocatore ottiene i 2/3 di probabilità contro l’1/3 iniziale che è rimasta sempre lo stessa. Teniamo, infatti, conto che l’avere aperto una porta con un capra, che doveva sicuramente esserci nelle due rimaste, non cambia assolutamente la probabilità della prima porta scelta. Se, invece, il conduttore, avesse scelto a  casaccio la porta finale del giocatore, la probabilità sarebbero state uguali al 50%. In questo caso la scambio di porta casuale avrebbe cambiato completamente la situazione e si sarebbe caduti nel caso banalissimo di due porte, una con l’auto e una con la capra…

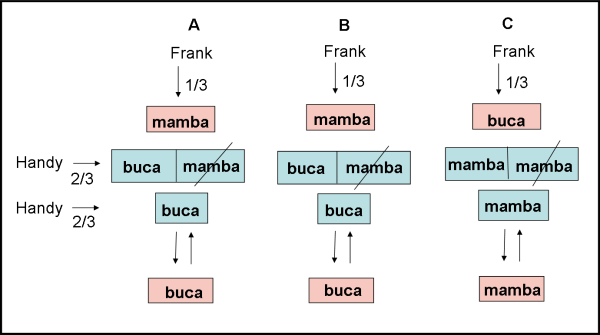
Riassumiamo con una figura la situazione con tutte le possibili configurazioni (3) e ciò che sembrerebbe paradossale diventa, invece, del tutto lampante e verificabile…

Frank ha tre sole possibilità (A, B, C): in A sceglie il mamba, in B anche, e in C la buca. (probabilità di scegliere la buca è pari a 1/3).

Handy ha a disposizione tre coppie di porte: in A ha un mamba e la buca, in B ha nuovamente il mamba e la buca, in C, ha due mamba. La sua probabilità di avere la buca è pari, ovviamente, a 2/3.

Entra in campo il giudice che elimina la porta con il mamba, cosa questa che non cambia assolutamente le probabilità di Handy, dato che era ovvio che nei tre casi ci fosse sempre almeno un mamba.

Handy ha tre possibilità: in A la buca, in B la buca e in C il mamba: proprio 2/3 di probabilità di avere la buca contro l’1/3 di Frank che è rimasto con la probabilità iniziale.

E’ quindi naturale che, cambiando la porta, Frank si ritrovi con due possibilità su 3 di avere la buca e Handy si debba accontentare di 1/3.