Il numero di Nepero è trascendente. Parte quarta.*****

Categorie: Matematica Scritto da: Umberto Cibien Commenti:0

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

Ricapitoliamo

Ricordo che dobbiamo dimostrare la falsità dell'eguaglianza:

P1+P2=0. Che è equivalente a dimostrare la falsità di:

$\fn_cm \fn_cm \fn_cm \frac{P_{1}+P_{2}}{\rho!}=\frac{P1}{\rho!}+\frac{P_{2}}{\rho!}=0$ .

Cioè:

$\fn_cm \fn_cm \fn_cm \frac{P1}{\rho!}+\frac{P_{2}}{\rho!}\neq 0$

per un certo valore di $\fn_cm \rho$ . Il primo termine è un intero, mentre vogliamo dimostrare che il secondo non lo è.

La dimostrazione continua.

Nell'ultima puntata di questa serie ,abbiamo dimostrato che P1, definito da:

$\dpi{120} \dpi{120} \dpi{120} P_{1}= a_{0}I_{\rho}(0)+a_{1}\cdot eI_{\rho}(1)+a_{2}\cdot e^{2}I_{\rho}(2)+....+a_{n}\cdot e^{n}I_{\rho}(n)$

è divisibile per $\fn_jvn \rho$ ! .

$\fn_cm I_{\rho}(0)$ = $\fn_cm \fn_cm \fn_cm \fn_cm \fn_cm \dpi{120} \pm (n!)^{\rho+1}\cdot \rho! + N(\rho+1)!$ dove N è un certo intero. (Infatti $\fn_cm I_{\rho}(0)$ si compone di un termine divisibile per $\fn_cm \rho!$ e di una somma di termini tutti divisibili per ( $\fn_cm \fn_cm \rho+1$ )!, per cui possiamo raccogliere ( $\fn_cm \fn_cm \rho+1$ )! )

i termini rimanenti che compongono P1 sono:

$\fn_jvn a_{1}\cdot eI_{\rho}(1)+a_{2}\cdot e^{2}I_{\rho}(2)+....+a_{n}\cdot e^{n}I_{\rho}(n)$

e abbiamo visto che sono tutti divisibili per ( $\dpi{120} \rho+1$ )!

Possiamo quindi scrivere :

$\fn_cm \fn_cm P_{1}=\pm a_{0} (n!)^{\rho+1}\cdot \rho! + a_{0}N(\rho+1)! + M(\rho+1)!$ dove M è un intero. Raggruppando possiamo compattare la scrittura:

$\fn_cm \fn_cm P_{1}=\pm a_{0} (n!)^{\rho+1}\cdot \rho! + Z(\rho+1)!$ dove $\fn_cm Z=M+a_{0}N$ è ancora un intero. Dividiamo adesso ambo i termini per $\fn_cm \rho!$

$\fn_cm \fn_cm \fn_cm \fn_cm \fn_cm \frac{P_{1}}{\rho!}=\frac{ \pm a_{0}(n!)^{\rho+1}\rho!}{\rho!}+\frac{Z(\rho+1)!}{\rho!}$ e semplificando:

$\fn_cm \fn_cm \dpi{120} \dpi{120} \frac{P_{1}}{\rho!}= \pm a_{0}(n!)^{\rho+1}+Z(\rho+1)$ e portando a primo membro $\fn_cm \pm a_{0}(n!)^{\rho+1}$ otteniamo:

$\fn_cm \fn_cm \fn_cm \fn_cm \fn_cm \frac{P_{1}}{\rho!}-(\frac{ \pm a_{0}(n!)^{\rho+1}\rho!}{\rho!})=Z(\rho+1)$ che significa:

$\dpi{120} \dpi{120} \frac{P_{1}}{\rho!}\equiv \pm a_{0}(n!)^{\rho+1}$ mod ( $\dpi{120} \rho+1$ ) *

ovvero che $\fn_cm \frac{P1}{\rho!}$ , $\fn_cm \pm a_{0}(n!)^{\rho+1}$ danno lo stesso resto divisi per $\dpi{120} \rho+1$ .

Il fatto che $\dpi{120} \dpi{120} \frac{P_{1}}{\rho!}\equiv \pm a_{0}(n!)^{\rho+1}$ mod ( $\dpi{120} \rho+1$ ) è molto importante, e ci permetterà di concludere la dimostrazione nell'articolo finale.

*( due numeri a, b sono equivalenti modulo z se e solo se la loro differenza è multipla di z)

Adesso che abbiamo finito con le proprietà di P1, veniamo a a P2:

$\dpi{120} \dpi{120} \dpi{120} \dpi{120} P_{2}= a_{1}\cdot eJ_{\rho}(1)+a_{2}\cdot e^{2}J_{\rho}(2)+....+a_{n}\cdot e^{n}J_{\rho}(n)$

Vogliamo dimostrare che per $\fn_jvn \rho$ abbastanza grande, $\fn_cm \fn_cm \frac{|P_{2}|}{\rho!}$ è un numero arbitrariamente piccolo. Riprendiamo la definizione dei $\fn_cm \fn_cm \dpi{120} J\rho(b)$ :

$\fn_cm \dpi{120} J\rho(b)=\int_{0}^{b}z^{\rho}[(z-1)(z-2)....(z-n)]^{\rho+1}e^{-z}dz$ .

Da adesso in poi lavoreremo con i valori assoluti.

Ricordo che una funzione continua definita in un intervallo chiuso ha sempre un massimo e un minimo. A noi , in questo conteso, ci interessa che esista un massimo.

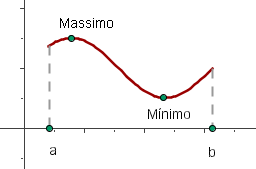
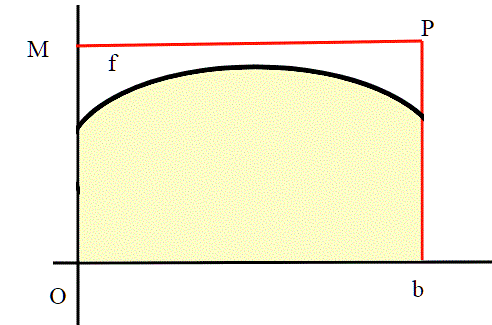
Consideriamo il massimo K di $\fn_cm \fn_cm |z(z-1)(z-2)....(z-n)|$ nell'intervallo [0,n] e il massimo $\fn_cm k_{1}$ di

$\fn_cm \fn_cm \fn_cm |(z-1)(z-2)....(z-n)e^{-z}|$ sempre in [0,n]. si ha:

$\fn_cm \fn_cm |z^{\rho}[(z-1)(z-2)....(z-n)]^{\rho+1}e^{-z}|\leq k_{1}K^{\rho}$ basta infatti moltiplicare membro a membro le le due diseguaglianze:

$\fn_cm \fn_cm \fn_cm \fn_cm \fn_cm |z(z-1)(z-2)....(z-n)|^{\rho}\leq K^{\rho}$

$\fn_cm \fn_cm \fn_cm \fn_cm \fn_cm |(z-1)(z-2)....(z-n)e^{-z}|\leq k_{1}$

consideriamo adesso i singoli integrali $\fn_cm \fn_cm \dpi{120} |J\rho(b)|\leq \int_{0}^{b}|z^{\rho}[(z-1)(z-2)....(z-n)]^{\rho+1}e^{-z}|dz$ per b=1....n

per ogni b avremo $\fn_cm \fn_jvn \fn_cm \fn_cm \dpi{120} |J\rho(b)|\leq bk_{1}K^{\rho}$ , visto che b è l'ampiezza dell'intervallo.

$\fn_cm \fn_cm \left\{\begin{matrix} |J\rho(1)|\leq 1\cdot k_{1}K^{\rho}\\ |J\rho(2)|\leq 2\cdot k_{1}K^{\rho}\\ .....\\ |J\rho(n)|\leq n\cdot k_{1}K^{\rho} \end{matrix}\right.$

Chiaramente l'area sottesa da una funzione f positiva limitata da un numero M è minore del prodotto M*b che è l'area del rettangolo OMPb che la contiene.

Sommiamo adesso tutti i membri di destra e di sinistra e poi poniamo $\fn_cm \fn_cm k_{2}=(|a_{1}|e +2 |a_{2}|e^{2}+....+ n|a_{e}|e^{n})\cdot k_{1}$

Otteniamo : $\fn_cm \fn_cm \fn_cm \dpi{120} \dpi{120} \dpi{120} \dpi{120} |P_{2}|=| a_{1}\cdot eJ_{\rho}(1)+a_{2}\cdot e^{2}J_{\rho}(2)+....+a_{n}\cdot e^{n}J_{\rho}(n)|<|a_{1}\cdot eJ_{\rho}(1)|+|a_{2}\cdot e^{2}J_{\rho}(2)|+....+|a_{n}\cdot e^{n}J_{\rho}(n)|$

ma quest'ultima espressione è minore di $\fn_cm \fn_cm (|a_{1}|e +2 |a_{2}|e^{2}+....+ n|a_{e}|e^{n})\cdot k_{1}K^{\rho}$ e la somma dentro parentesi è proprio $\fn_cm k_{2}$ .

Concludiamo allora che $\fn_cm \fn_cm |P_{2}|\leq k_{2}K^{\rho}$ , e quindi $\fn_cm \frac{|P_{2}|}{\rho!}\leq \frac{k_{2}K^{\rho}}{\rho!}$ .

Il termine di destra può assumere valori molto piccoli al crescere di $\fn_cm \rho$ . Ma lo vedremo in dettaglio nella prossima parte, che sarà anche quella finale.

L	M	M	G	V	S	D
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31

Il numero di Nepero è trascendente. Parte quarta.*****

Articoli correlati

Soluzione del "banale" esponente **

(Q) Un semplice esponente ... **

Soluzioni dello scontro evitato **/***

Evitiamo uno scontro **/***

Lascia un commento Cancel Reply

Soluzioni dello scontro evitato /*

Evitiamo uno scontro /*