Categorie: Matematica
Tags: geometria Nobody pappidi Pappo percorso minimo quiz
Scritto da: Vincenzo Zappalà
Commenti:34
A spasso dentro una circonferenza ***
Avevate pensato di non incontrarli più? Sbagliato! Ecco di nuovo Pippo, Pappo e Peppa alle prese con Nobody, sempre più perverso (malgrado le promesse). Un semplice (ma forse non troppo) problemino di geometria euclidea (finalmente!).
In attesa di qualche bella news e della prima stella che ci racconterà la sua vita, mi sembra giusto tornare a qualche problemino di geometria (è tanto che li abbiamo sospesi,,,). La soluzione è semplice, ma abbisogna di un qualcosa di non banalissimo... inoltre, non è detto che la mia sia la soluzione migliore!
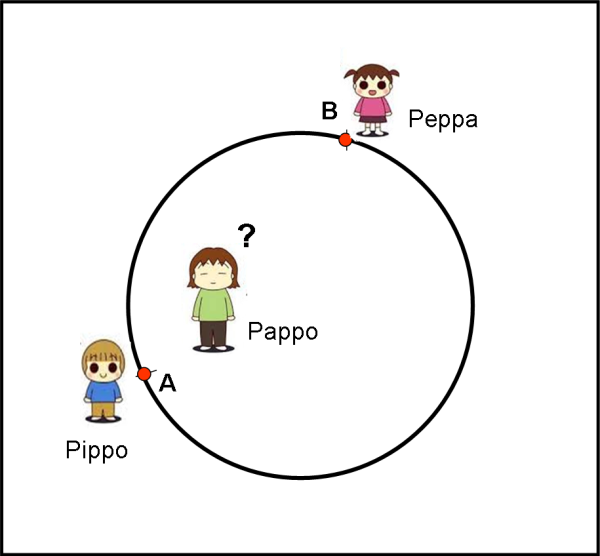
Nobody riesce a catturare con uno stratagemma sia Pippo che Peppa e li lega saldamente in due punti di un muro che limita un grande cortile di forma perfettamente circolare. Poi chiama Pappo e gli dice che libererà sua sorella e suo fratello solo se calcolerà esattamente il raggio del cortile.
Per poterlo fare, permette a Pappo di misurare il percorso che compie per andare da Pippo a Peppa camminando dentro al cortile sempre in linea retta e avvicinandosi sempre di più a Peppa. Non può, perciò, assolutamente proseguire dopo che ha raggiunto la sorella o allontanarsi da lei. E’ libero di scegliere il tragitto e di cambiare direzione quante volte vuole, ma solo di un angolo di 90°. Pappo ha a disposizione solo un metro rigido molto lungo (ma decisamente minore del raggio) e una squadretta che gli permetta, nel caso, di cambiare direzione in modo ortogonale rispetto al tragitto compiuto precedentemente. Inoltre, non può percorrere due volte lo stesso tragitto.
Pappo ci pensa un attimo e poi dice: “Lo farò senz’altro e utilizzerò il percorso più corto possibile. Ti sfido, infatti, a riuscirci con un percorso minore del mio, con quei piedoni enormi che hai! Se non ci riuscirai devi giurare di non molestarci più”. Nobody ridacchia e poi accetta la sfida. Conoscendo Pappo, però, la sua risata è un po’ trattenuta...
Si chiede:
(1) Che tipo di percorso deve fare Pappo per andare da Pippo (A) fino a Peppa (B) per potere calcolare il raggio r ? (rivolta ai teorici)
(2) Perché è così sicuro di utilizzare il percorso minimo possibile? (rivolta a chi ama le cose pratiche, tipo ingegneri giocatori di golf o costruttori di meridiane)
(3) Scrivere la relazione che lega il raggio ai tratti rettilinei utilizzati, cercando di semplificarla al massimo (rivolta ai matematici)
QUI la soluzione






34 commenti
Carissimo Prof, due interrogativi:
Riconosco che una risposta affermativa a queste due domande faciliterebbe di molto il problema, ma meglio esserne certi
Gent.mo Ing.
In effetti, le tre stelle facevano intuire che non poteva essere così semplice. Infatti, sarebbe bastato partire da A in una qualsiasi direzione , procedere in linea retta fino a incontrare la recinzione del giardino. Da quel punto, proseguire poi a 90 gradi (con l'uso della squadra) in linea retta fino a incontrare di nuovo la recinzione nel punto C. Per costruzione, quindi, i punti A e C sarebbero stati gli estremi del diametro della recinzione circolare , che avremmo calcolato subito con il teorema di Pitagora (avendo precedentemente misurato i due cateti con il metro a disposizione). Ma, dovendo Pappo partire da Pippo e arrivare necessariamente a Peppa, la cosa si complica non poco e quanto da me sopra scritto serve solo confondere le idee. Sorry
Il percorso di Pappo, che deve muoversi avvicinandosi sempre di più a Peppa , potrebbe essere quello disegnato nella figura ACDB
Prende come origine degli assi xy il punto A quindi le coordinate di A sono (0,0)
Il punto C avrà coordinate (0, AC)
Da C si muove orizzontalmente fino a D (allineamento con B) e verticalmente fino a B
il punto B avrà coordinate (CD, AC+DB)
L'equazione del cerchio passante per i tre punti A , B , C è la seguente
Pappo dovrà sostituire a x e y i valori delle coordinate di A B C ottenendo tre equazioni in cui le tre incognite sono a b c
A esempio, dalla prima sostituzione con i valori di coordinate di A
sostituendo le coordinate di B e C...
dalla prima equazione ricavo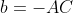
Sostituendo b nella seconda equazione ricavo a
Noti i valori di a , b ,c si può ottenere immediatamente il raggio
effettivamente... ma Pappo dice che può usare il metodo facendo praticamente il minimo percorso in assoluto...
prova con AC non verticale... e senza introdurre equazioni (Pappo non le conosce ancora...)
Vedo di seguire le tue indicazioni, però....
Se non ci fosse il vincolo di DOVER raggiungere Peppa, il percorso sarebbe brevissimo....
Il percorso inizia da A, perpendicolarmente alla circonferenza e va in C, con distanza = lp (il metro deve essere molto preciso ...)
Perpendicolarmente si sale da C a D
Da D si va in E ancora con distanza lp
Perpendicolare fino all'ultimo punto F.
Stesso ragionamento visto prima, Avendo tre punti ADF sulla circonferenza, di coordinate note con distanza totale esigua.
Se ho a disposizione una squadra, allora posso partire da A in direzione perpendicolare alla tangente in A alla recinzione (basta posizionare la squadra in maniera che uno dei suoi lati sia tangente al cerchio). Se tale possibilità non è ammessa, potete evitare di leggere il seguito
Proseguo lungo la suddetta direzione (avvicinandomi così a Peppa) fino a quando, sempre con la squadra, non traguardo Peppa. Chiamo tale punto C. Ovviamente, essendomi mosso lungo la perpendicolare alla tangente alla recinzione, sarò passato dal centro, senza però saperlo. Ora, da C mi muovo verso Peppa fino a raggiungerla. Chiamo p e q le lunghezze dei due tratti AC e CB percorsi, misurati con il metro. Considero il triangolo ABH, chiamando con H l'intersezione del prolungamento di AC fino a incontrare la recinzione (in pratica l'estremo del diametro AH). Tale triangolo è ovviamente rettangolo. Considero ora i due triangoli, anche essi rettangoli, ACB e HCB. Essi sono pure simili, allora posso scrivere :
AC/CB = CB/CH
cioè:
p/q=q/(2R-p)
da cui si ottiene :
R=((q^2/p)+p)/2
Propongo questa impostazione:
Pappo percorre l'arco da A a B con tratti a scalinata di 90°. la somma di tutti i tratti paralleli alla corda fornisce la lunghezza C della stessa ( AB = 2AC) , mentre la somma dei moduli dei tratti verticali fornisce 2S, ossia il doppio della misura della Saetta (2DC).
L'angolo a=arctg(DC/AC) è quindi noto
Benché non si conosca il punto O, si ricava facilmente l'angolo c
Infatti b= 90-a e c = 180-2b = 2a
dalla relazione tra la semicorda AC e il raggio R , ossia AC=R sen c ricavo il raggio R
R= AC/senc
Se non si può usare neanche un pochino di trigonometria, allora...
Il procedimento è lo stesso descritto nel post precedente fino ad individuare le misure di AC e DC
La distanza AD è calcolabile come ipotenusa del triangolo rettangolo ACD di cui sono noti i cateti.
Per il punto E, medio di AD, passa la bisettrice dell'angolo c
Sappiamo che l'angolo b = 90-a e che l'angolo c= 180-2b = 2a
Il triangolo rettangolo OED è quindi simile ad ACD, pertanto il rapporto tra ipotenusa e cateto minore è lo stesso.
AD / DC = OD/ DE Dato che DE = AD/2, AD/DC = 2 OD/AD OD è il raggio cercato, R e lo ricavo
R= AD^2/2 DC =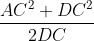
La lunghezza del percorso che segue il profilo dell'arco, sommando i segmenti paralleli e perpendicolari alla corda, è la somma della distanza AB + 2DC.
Nel caso che la corda abbia lunghezza pari al lato del quadrato inscritto nella circonferenza la somma AB+2DC vale&space;=&space;R\sqrt{2}&space;+R\sqrt{2}(\sqrt{2}-1)&space;=2R)
Questa è la stessa distanza 2R che si ottiene sommando le proiezioni della corda sugli assi perpendicolari passanti per il centro, ossia la soluzione proposta da Arturo. A seconda che le corde siano più lunghe o più corte di questa particolare corda, il percorso minimo si otterrebbe (credo) ora con una, ora con l'altra soluzione. Ad esempio nel caso di una corda più corta, come il lato dell'esagono inscritto nella circonferenza, ossia lunga come il raggio, il percorso delle proiezioni sugli assi dovrebbe risultare più lungo. Al contrario, con una corda lunga come il lato del triangolo equilatero inscritto, il percorso lungo le proiezioni sugli assi risulterà più breve.
Se poi Pappo, eseguendo le sue misure, percorresse la linea spezzata formata da tutte le piccole ipotenuse che approssimano la curva dell'arco di cerchio, insomma, "camminasse lungo le ipotenuse" usando la squadra per misurare i cateti, la distanza percorsa lungo l'arco risulterebbe inferiore a quella delle proiezioni della corda sulle coordinate scelte da Arturo anche per alcune corde più lunghe di quella del lato del quadrato inscritto.
Infatti, se la corda avesse proprio la lunghezza del lato di un quadrato inscritto nella circonferenza, il percorso lungo gli assi avrebbe lunghezza 2R, mentre lungo l'arco sarebbe più breve, pari a R pi/2.
Tutto quanto, ovviamente , da verificare con maggiore accuratezza.
dunque, nessuna tangente esterna (c'è un muro!). Seguire la corda a pezzettini (non ho ben capito li significato delle varie lettere... riscrivi per bene) non si avvicina certo al minimo percorso, nessun angolo misurabile se non 90° e, poi, riscrivi tutto stando attento alle lettere e spiegando meglio... Ma poi raggiunge Peppa? Raggiungere Peppa è un obbligo fondamentale... e decisivo.
I am sorry...
Piccolo aiuto...
leggete bene le mie risposte e poi vi chiedo: "Qual è il minimo percorso fattibile?", dovete avvicinarvi a quello il più possibile...
Il minimo percorso per andare da A a B è la corda AB.
Percorrendola senza deviare si ricava solo l'informazione sulla sua lunghezza, insufficiente per trovare il raggio.
Iniziando a percorrerla da A, nel momento in cui ci si allontana dalla corda a 90°, la distanza da B aumenta, infrangendo la regola che ci si deve sempre avvicinare.
Quindi la direzione iniziale non può essere quella della corda AB né quella della perpendicolare alla circonferenza. Dalla primo post abbiamo anche escluso la direzione verticale e la possibilità di usare equazioni.
Da escludere anche la trigonometria? Immagino di si.
Dovendo partire da A secondo una direzione che comunque avvicina Pappo al punto B, e poiché il percorso tra quelli fattibili deve essere tale da permettere di determinare il raggio della circonferenza, direi che le direzioni possibili sono le rette che passano da A, intersecano la circonferenza e formano con l'asse x un angolo compreso tra quello della corda AB e quello della tangente alla circonferenza nel punto A. Considerando una qualsiasi di queste direzioni, procedendo fino a incontrare la circonferenza in un punto X , poi svoltando a 90 gradi e proseguendo fino a traguardare a 90 gradi il punto B per poi , infine, raggiungerlo, non mi viene tuttavia un'idea su come determinare il raggio. A meno che non prenda, tra queste direzioni, quella parallela al raggio passante per B. In tal caso saprei come calcolare il raggio [ = ((p^2/q)+q)/2 indicando con p e q le lunghezze misurate del secondo e terzo tratto del percorso, espressione praticamente identica a quella che avevo scritto prima] e il percorso risulterebbe pure il minimo tra quelli relativi a tali direzioni . Ma, ahimè, non essendo visibile il centro, non posso stabilire quale è la direzione parallela al raggio passante per B. Comunque, non credo sia un caso che il valore minimo della lunghezza del percorso che trovo in questo caso sia identico a quello che ho trovato prima considerando la perpendicolare alla tangente nel punto A.
Attendiamo idee migliori.
(incidentalmente, essendomi fissato con un uso perverso della squadretta, ho notato che potrei comunque determinare la perpendicolare alla tangente alla circonferenza nel punto A anche in presenza di un muro invalicabile. Ma questa è un'altra storia )
)
forza ragazzini ... non siete lontanissimi. Anzi... qualcosa di giusto c'è stato e l'ho anche detto... leggete bene nei commenti...
e vorrei la relazione tra r e i tragitti effettivamente compiuti da Pippo per raggiungere Peppa...
Vi posso assicurare che basta il teorema di Pitagora.... e qualche similitudine qua e là...
E poi mi piacerebbe che rendeste minima una certa cosa, ma lì c'è da pensarci sopra...
Cari Enzo e Arturo. tra poco mi devo mettere in auto e quindi stop ai quiz fino a stasera, anzi a domani sera, causa assemblea condominiale che si annuncia tumultuosa.
Intanto, metto questa figura che magari può aiutare ( o essere fuorviante, chissà)
Pappo va da A verso C , quando è in quadratura con B gira di 90° a sinistra e va fino a B.
M è il punto medio di AB, quindi noti AC e CB, MB è calcolabile come metà ipotenusa.
Il centro O si trova sulla perpendicolare ad AB in M
OB è il raggio cercato
MC è uguale a MB, quindi noto ( i punti BCA appartengono alla circonferenza che ha diametro AB e centro in M)
OB ed MC sono le diagonali del quadrilatero OMBC
Da qui in poi occorre fare qualche ragionamento su similitudini di triangoli che lascio all'amico Arturo.
Pappo percorre la corda da A a B, poi torna indietro fino a metà corda e percorre perpendicolarmente il tratto dalla corda alla circonferenza
c=corda
f=tratto perpendicolare alla corda fino alla circonferenza
f è parte del raggio di misura «r» da calcolare perpendicolare alla corda, insieme ad altri due raggi che hanno gli estremi sulla circonferenza coincidenti con gli estremi della corda, si viene così a creare un triangolo rettangolo con ipotenusa il raggio da calcolare come cateto mezza corda, l’altro cateto è pari al raggio diminuito della componente f, pertanto possiamo calcolare applicando pitagora:
r²=(c/2)²+(r-f)²
quindi
r²=c²/4+r²+f²-2rf
2rf= c²/4+f²
Quindi
r=c²/8f+f/2
caro Mauro,
ti fermo subito...
tu scrivi: "Pappo percorre la corda da A a B e poi torna indietro fino a metà corda..."
Nel quiz si dice chiaramente: "non può percorrere due volte lo stesso tragitto"
mi spiace... devi cambiare procedimento...
Partendo da A percorro un tratto nella direzione verso B. Più avanti vediamo quanto può essere la lunghezza di questo tratto.
Alla fine del tratto devio di 90° verso la circonferenza fino a raggiungerla. Chiamo h la lunghezza di questo tratto.
Devio nuovamente di 90° fino a raggiungere la circonferenza, percorrendo quindi una corda parallela ad AB.
A questo punto devio di 90° a destra e percorro una lunghezza h. Devio a sinistra di 90° mettendomi nuovamente sulla direttrice AB che percorro fino a raggiungere B.
Dalle lunghezze dei tratti percorsi posso ricavare le lunghezze delle due corde parallele che chiamo c1 e c2 e la loro distanza h. Queste tre grandezze sono legate tra loro e con il raggio da questa relazione
Che si può risolvere in R ottenedo
Tra i percorsi possibili il percorso più corto è quello che devia di meno dalla congiungente A e B, quindi quello con il minimo h.
Di conseguenza il primo tratto dovrebbe essere il più corto possibile, compatibilmente con i vincoli che sono dati e con la precisione della misura. Teoricamente può essere reso piccolo a piacere a meno che non ci sia il vincolo di percorrere in linea retta una lunghezza non superiore a quella del regolo.
Allora il percorso minimo è quello con c2 di lunghezza massima, cioè corrispondente alla lunghezza del regolo, almeno nel caso di un regolo abbastanza lungo da poter realizzare il percorso in figura.
caro Fabry,
sarebbe perfetto, ma... come fa Pappo a dirigersi verso Peppa con esattezza (l'esattezza è richiesta , altrimenti non valgono le varie relazioni...)? Io avevo detto nel testo: "... un metro rigido molto lungo (ma decisamente minore del raggio)...". L'hai detto tu stesso : "avendo un regolo abbastanza lungo...", ma non lo è...
aggiungo, per correttezza, che è proprio per questo problema che Pappo dice a Nobody che si potrà avvicinare moltissimo al percorso minimo, ma non raggiungerlo veramente... In ogni modo, avere i piedi piccoli può servire se si ha un buon occhio...
PER TUTTI: e pensare che Euclide non avrebbe avuto problemi (senza equazioni e trigonometria)
Il percorso è formato da quattro segmenti
AC + CD + DE + EB per ciascuno di essi viene registrata la misura.
Da A alla circonferenza in C, poi gira di 90° a destra e si muove verso D (registra la distanza CD) . Prosegue fino ad essere in quadratura , quando è in E, con il punto B , gira di 90°a sinistra e giunge fino a B ove si ferma.
L'ipotesi è che Pappo sia in grado di valutare quando si trova allineato contemporaneamente con il punto A e il punto B, nel momento in cui è nel punto D. Inoltre deve capire di trovarsi in quadratura con la direzione verso B, nel momento in cui passa per il punto E
Il punto F è intermedio tra C e B e per esso passa la bisettrice dell'angolo COB che è il doppio dell' angolo CAB
I segmenti OB e OC sono uguali al raggio cercato R.
I due triangoli rettangoli ACD e OFC sono simili. Quindi ne consegue che il rapporto tra le ipotenuse è lo stesso del rapporto tra i cateti.
OC/AD = CD/CF
OC =R = CD*AD/CF = CD* radq(AC^2 + CD ^2) * 1/ ( 1/2 radq((CD+DE)^2 + EB^2))
.... in questo momento LATEX non è accessibile ....
Il raggio risulta espresso in funzione dei soli dati misurati durante il percorso
Per ridurre la lunghezza del percorso l'angolo iniziale con la direzione AB deve essere il più piccolo possibile. in modo da arrivare a toccare la circonferenza a brevissima distanza dal punto B.
La valutazione delle misure dei segmenti CD DE ed EB diventa però molto critica
Se non è possibile proseguire lungo la direzione iniziata oltre una data misura, inferiore al raggio, nel disegno il punto C andrà fatto scivolare sulla circonferenza verso il punto A , finché AC avrà la lunghezza imposta,
Il collegamento dei vari punti segue comunque la stessa logica, e le considerazioni del calcolo restano le stesse.
In realtà nel testo si dice che il cambio di direzione è facoltativo e non imposto.
Per questo mi aspettavo che l'obiezione alla soluzione di Fabrizio fosse sul fatto che , deviando di 90° dalla retta AB, la distanza da B andava aumentando e non diminuendo.
Vedo che invece è stato contestato il vincolo sulla lunghezza del righello , come se fosse obbligatorio girare di 90° alla fine del righello. (questo non mi era chiaro in partenza).
Latex continua ad essere latitantex...
caro Mau,
l'obiezione su Fabrizio era anche giustamente quella dell'allontanamento, ma il regolo può essere usato solo per proseguire in linea retta, ma non certo per arrivare al punto finale. Non per niente il primo pezzo va fatto a casaccio e ad occhio in modo da arrivare più vicini possibili a B. Poi è tutta questione di brevi distanze, addirittura misurabili con la sola squadretta. Anzi il limite dipende proprio da quanto riesci a rendere piccoli gli ultimi tragitti, I piedoni di Nobody sono meno adatti...
Tuttavia, ho ancora un problema sulla tua soluzione: mentre accetto che capisca quando è in E (va avanti lungo il regolo, si ferma, inserisce la squadretta e questa dovrebbe bastare a misurare EB. Se non è ancora in E, va avanti centimetro per centimetro fino al punto E esatto, non mi torna la decisione di essere nel punto D. La distanza DA è troppo lunga per il regolo e ricadiamo nell'ipotesi di Fabrizio (a parte l'allontanarsi...).
Si può fare ancora meglio...
Forza e pensiamo al grande Euclide (meno conosciuto- ma non ce ne sarebbe nemmeno bisogno)
In attesa di Euclide, posso rinunciare al punto D.
Il percorso è di 3 elementi: AC + CE +EB
La distanza AB è l'ipotenusa di un triangolo rettangolo che ha cateti AC+EB e CE, che è simile al triangolo rettangolo CFO.
AB= radq((AC+EB)^2 + CE^2)
CFO ha cateti CF e FO e ipotenusa = CO (raggio cercato)
CF = 1/2 radq(CE^2 + EB^2)
rapporto ipotenuse = CO/AB = rapporto cateti = CF/CE da cui ricavo CO (raggio cercato)
CO = AB* CF/CE = radq((AC+EB)^2 + CE^2)* 1/2 radq(CE^2+EB^2) / CE
Se faccio in tempo aggiungo una figura nuova (senza il punto D)
Ecco la figura
E l'espressione di R in funzione dei tratti del percorso
R=CO = AB* CF/CE = radq((AC+EB)^2 + CE^2)* 1/2 radq(CE^2+EB^2) / CE
Mi devo fermare qui, sperando non ci siano errori.
Adesso tocca a Euclide...
bene... bravo Mau... manca solo la pare matematica finale, ma devo dire che ci sei arrivato anche se in modo un po' diverso dal mio. Ma io sono più vecchio e legato ai vecchi... Ah... Euclide e il teorema delle corde! Non se lo ricorda più nessuno!
Scusate, ma non riesco a trovare un modo per dimostrare che i triangoli AGB ed OCF sono simili.
Anzi, pensando che per essere simili dovrebbero avere gli angoli uguali e che il punto A può essere in una posizione arbitraria, se fossero simili dovrebbero essere simili anche tutti i triangoli costruti come AGB a partire da un diverso punto A' con gli stessi punti B e C. Cosa che non mi torna poichè l'angolo in A' cambierebbe dovendo passare sempre per B e C.
Forse c'è qualcosa che non ho capito della costruzione?
I due triangoli sono ambedue rettangoli.
Dal centro O , la corda CB è vista sotto un angolo doppio di quello con cui è vista dal punto A, sula circonferenza.
Ossia COB = 2 CAB
Quindi l'angolo COF, che è la metà dell' angolo COB, risulta uguale all'angolo CAB, che è anche GAB
I due triangoli GAB e COF hanno pertanto gli stessi angoli.
Maurizio, quello che dici sugli angoli in A e O è certamente valido quando F, O ed A sono allineati. Ma è valido anche quando A è posizionato diversamente. come nel nostro caso? Significherebbe che comunque posto A, vederebbe il segmento CB sempre sotto lo stesso angolo.
Sì, Fabrizio, tutti gli angoli alla circonferenza che insistono sullo stesso arco sono tra loro congruenti in quanto tutti sono la metà del corrispondente angolo al centro, insistente sullo stesso arco.
Pensa solo al caso di un arco pari alla semicirconferenza... l'angolo al centro vale 180° e tutti i punti della circonferenza vedono il diametro (la corda della semicirconferenza) sotto un angolo di 90°, cioè la metà di 180°.
Non si tratta di un caso particolare, ma vale per qualsiasi arco.
Puoi vederla così...se cambi il punto alla circonferenza, le due linee ruotano attorno agli estremi della corda del medesimo angolo.
Ma esistono dimostrazioni formali di questa proprietà.
Maurizio, hai ragione!
Una dimostrazione trigonometrica sono riuscita a ricavarla.
Grazie della spiegazione.
Bene, bene... penso che possa iniziare a scrivere la mia soluzione, che, ovviamente, non è molto diversa, ma fa uso di un bel teorema spesso dimenticato (ma che si dimostra subito)...
Niente di che, Fabrizio, ero certo che in pochissimo tempo avresti ricavato una dimostrazione rigorosa, come è stato.
A parte la geometria, il fatto che mi incuriosisce è che, anche per me , "intuitivamente" sembra strano che l'angolo resti uguale al variare del punto sulla circonferenza.
Per qualche motivo si è indotti a pensare che allontanandosi dalla posizione centrale, sull'asse della corda, l'angolo debba ridursi.
Credo di aver trovato una possibile spiegazione "psicologica" in questa figura:
La prima idea che viene in mente è quella raffigurata nel quadrato giallo. Penso alla base AB e al triangolo ABC, (l'ho disegnato quasi fosse equilatero). I vari spostamenti da C in C' , C " riducono progressivamente l'angolo da 60° a 45° e, proseguendo nello slittamento verso destra, a valori sempre inferiori.
Questo perché seguiamo mentalmente, implicitamente, il tracciato della linea retta parallela alla base AB.
E' la curvatura della circonferenza, nella figura a sinistra, che "accomoda" le cose e mantiene costante l'angolo in C, C', C".
Ma evidentemente il nostro istinto ( almeno il mio) è più orientato e abituato a pensare lungo linee rette che lungo linee curve.
Maurizio, mi ero fatto ingannare dalla stessa intuizione errata che hai descritto.
Il fatto che mi ha fatto ricredere ancor prima della dimostrazione è pensare alla situazione al limite, quando il C della tua figura tende a sovrapporsi a B. Proprio la situazione dove intuitivamente ero portato a credere che l'angolo diventasse sempre più piccolo fino ad annullarsi. Pensandoci bene però, in questo caso un lato tende a coincidere con AB e l'altro lato tende a diventare tangente alla circonferenza in B. E' facile vedere che anche nella situazione limite l'angolo è ancora pari al semiangolo in O.