Questo articolo, diviso in due (o più?) parti vuole ricostruire l'origine delle prime ricerche dedicate agli asteroidi doppi. In particolare, parlerò del mio primo modello che  rappresenta l'inizio di successive indagini teoriche in cui vennero rapidamente inserite le famose "pile of rubble", rese celebri molti anni prima nientedimeno che da Paperino e da Zio Paperone. Per molti anni ci dovemmo accontentare di teorie fino a che il flyby della sonda Galileo, nel 1993, non scoprì Dattilo, il piccolo satellite dell'asteroide Ida, che diede una conferma definitiva a un'idea quasi dimenticata e che fece tornare in auge molte delle caratteristiche previste per la scoperta degli asteroidi doppi, oggi considerati una quasi normalità.

Tutto nasce nel 1978 quando l’occultazione di una stella da parte dell’asteroide Herculina fece un vero “scoop”: l’asteroide di 216 km di diametro sembrava avere un satellite di 46 km che orbitava a circa 1000 km di distanza. Si parlò di conferme e di quasi certezza, al punto che, durante una Scuola di Meccanica Celeste tenutasi a Cortina, il grande Bepi Colombo mi si avvicinò e mi diede la notizia della scoperta, incitandomi: “Avanti, buttati a pesce sugli asteroidi doppi” (probabilmente usò altre parole, ma il succo fu quello)". In particolare, lui non vedeva nessun problema dinamico nella configurazione e... se lo diceva lui!

Poi il satellite di Herculina svanì nel nulla (lo cercò inutilmente perfino il telescopio Hubble, molti anni più tardi), ma ormai mi aveva fatto nascere un'idea fissa: “se esistono asteroidi doppi dovrebbe non essere impossibile capirlo anche attraverso la curva di luce”. In fondo ci trovavamo di fronte a un mini sistema binario stellare con tanto di transiti della primaria da parte della secondaria e viceversa. Oggi sembra ovvio, ma allora era una specie di perdita di tempo...

Tuttavia, anche se molto più piccoli, gli asteroidi presentano due problemi aggiuntivi, veramente grandi. Il primo è legato alla loro forma irregolare (a cui si possono aggiungere macchie di albedo). Una stella brilla di luce propria e, inoltre, a parte le variabili intrinseche, la sua luminosità non cambia (assomiglia proprio a una sfera!). Se essa è singola la sua luminosità non può che tradursi in una curva di luce orizzontale. Se invece è doppia e la secondaria ha un piano orbitale inclinato di poco rispetto alla nostra linea di vista, è facile che la traccia di luminosità rettilinea sia relativa alla somma delle due luminosità, ma che poi subisca una caduta quando la compagna le passa davanti o dietro (Fig. 1).

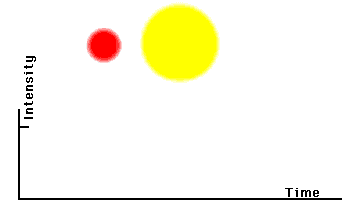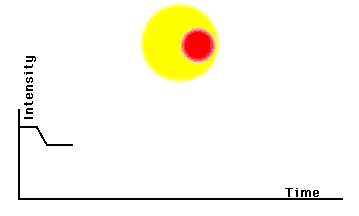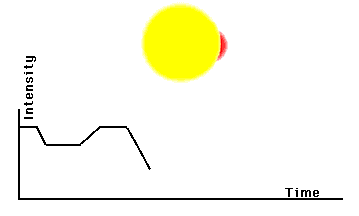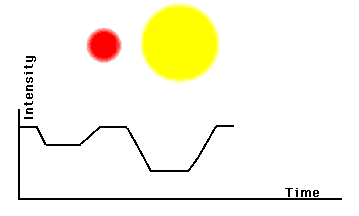
Se le due stelle hanno la stessa luminosità avremo una curva di luce con i due minimi uguali. Normalmente ciò non è vero e i due minimi hanno profondità diverse. Ovviamente, più le stelle sono vicine e più è facile vedere le mutue eclissi o transiti che dir si voglia. La curva di luce può anche diventare una specie di sinusoide se le stelle sono praticamente a contatto e il tempo in cui si vedono  entrambe diventa sempre più corto. Se, inoltre, le due stelle si deformano e si allungano per effetti mareali o per rotazione molto rapida, la curva di luce diventa una perfetta sinusoide.

Le forme possono variare anche in base al diametro relativo delle due stelle e/o alla totalità delle due eclissi: i minimi possono anche essere praticamente piatti o a punta. La Fig. 2 illustra qualche  esempio. Beh… un bel numero di possibilità, ma la duplicità è assodata.

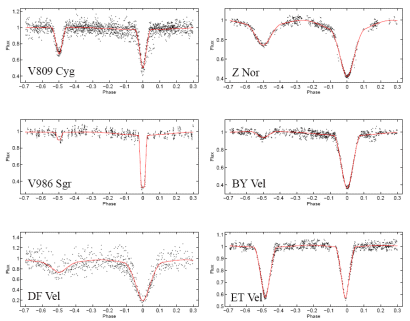
Passiamo adesso agli asteroidi e ai loro problemi aggiuntivi. Innanzitutto, come già più volte ripetuto, la loro forma non è regolare e l’area apparente può variare di molto. Se l’oggetto avesse una forma assimilabile a un ellissoide a tre o due assi avremmo una curva sinusoidale molto simile alle stelle binarie strette. Il che vorrebbe dire che una sinusoide potrebbe anche implicare un sistema di asteroidi sferici quasi a contatto o addirittura a contatto. Un caso classico è quello di Ettore e di Kleopatra.

Tuttavia, due massimi e due minimi più o meno ripidi o staccati potrebbero anche essere dovuti a forme più bizzarre, come abbiamo visto QUI, in modo molto semplificato. Sperare di riconoscere un asteroide doppio quasi a contatto è un grosso problema, a meno di non fare calcoli di densità e rifiutare quelli che darebbero risultati assurdi (cosa che facemmo in seguito).

Oggetti doppi regolari o oggetti singoli dalle forme molto strane? Se pensiamo a quanto fossero primitive le tecnologie di allora (con un 40 cm si riuscivano a osservare con un fotometro fotoelettrico oggetti di magnitudine non superiore alla 12-13) la risposta non era molto semplice (e non lo è nemmeno oggi). Tuttavia, poter osservare soprattutto asteroidi piuttosto luminosi (e quindi, mediamente, gradi) poteva rappresentare un punto a favore. Essi avrebbero potuto avere forme più regolari se non addirittura quasi sferici o, al limite, ellissoidali.

La faccenda, però, non finiva lì… gli asteroidi riflettono la luce del Sole e se qualcosa passa davanti al Sole causa una vera eclissi, proiettando un'ombra scura. Il Sole può  formare un certo angolo rispetto alla Terra se visto dall’asteroide (l’angolo di fase), quello che ci fa vedere la Luna sia Piena che Nuova che come una falce. Gli asteroidi sono lontani e quest’angolo non può superare un certo valore, ma quanto basta per creare una piccola falce nera al bordo dell’asteroide principale. Tuttavia, ancora peggio (o meglio), il satellite potrebbe proiettare la sua ombra sul corpo primario, oltre che passargli davanti. Un qualcosa che già conosciamo bene per le eclissi e i transiti dei satelliti di Giove.

Un grosso problema che le stelle non hanno… ma che potrebbe anche essere un vantaggio! Se il gioco combinato delle ombre e dei transiti comportasse delle strane configurazioni, esse potrebbero essere dei segnali per far pensare a un sistema doppio non a contatto e con il secondario anche abbastanza più piccolo del primario (sicuramente, però, di grandezza relativa ben maggiore di quella dei satelliti medicei rispetto a Giove!)

E, allora, perché non provare a simulare una situazione del genere, cambiando l'angolo di fase α e vedere che cosa veniva fuori? Una cosa non certo difficile, ma a cui non si era mai veramente pensato. Eccomi perciò seguire il consiglio di Bepi Colombo e prendere un enorme foglio di carta quadrettata, spostarmi in uno dei due grandi tavoli del corridoio della biblioteca e via con le simulazioni geometriche, accompagnate da qualche calcolo (che in gran parte tralascio in questa sede). Il direttore, Mario G. Fracastoro, passava, scrollava un po’ il capo, ridacchiava e mi dava del mezzo matto ma, in fondo, era piuttosto interessato, essendo uno specialista delle stelle doppie ad eclissi.

Vi assicuro che come gioco geometrico non era niente male, anche se il primo tentativo simulava una configurazioni estremamente semplice, e mi permise di diventare amico e collaboratore di  Ed Tedesco del Lunar and Planetary Laboratory di Tucson che stava tentando un simile procedimento, molto più tecnologico (all'americana) del mio sistema con riga, goniometro e compasso… Ma poi i risultati coincidevano e iniziammo a scambiarci le idee (attraverso lettere… dieci giorni per arrivare e dieci per ritornare).

Un lavoro non certo fondamentale, ma che segnava, comunque, l’avvio della ricerca sia osservativa che teorica dei sistemi binari asteroidali e che permetteva -forse- di scovarli utilizzando le sole curve di luce.

Per molto tempo gli asteroidi doppi rimasero una nostra illusione, ma poi, finalmente, eccoli comparire alla grande con Ida e il fratellino Dattilo! Beh… posso dire: “Ted ed io l’avevamo sempre detto e creduto”.

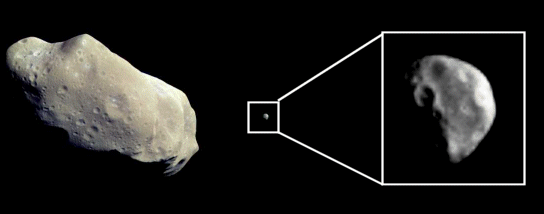
Senza formule e con la sola strategia geometrica voglio raccontarvi questa piccola avventura pionieristica, che mi diede, comunque, una grande soddisfazione…

Iniziamo considerando l'effetto puro e semplice dei transiti del satellite.

(1) I transiti

Bene scegliamo le in modo ultra semplificato le caratteristiche del nostro sistema doppio, formato da due sfere di raggio R e r, a una distanza reciproca uguale a d (orbita circolare, ovviamente, e piano orbitale coincidete con quello  equatoriale):

R/r = 6

d/r = 16

Devo far notare che questi numeri erano già stati scelti proprio per un caso particolare che vedremmo più tardi.

Per iniziare, mettiamo la fase solare uguale a zero, ossia consideriamoci perfettamente all’opposizione e, inoltre, immaginiamo di vedere l'oggetto in  modo perpendicolare al suo asse di rotazione. Due requisiti non impossibili da ottenere. Durante la sua orbita attorno al Sole, un oggetto (qualsiasi sia la direzione del suo asse) deve potersi vedere, prima o poi, con vista equatoriale (tranne casi particolari legati alle risonanze orbitali), così come è anche facile osservarlo a un angolo di fase praticamente uguale azero.

Beh… la faccenda è piuttosto facile da descrivere. Le ombre sia del secondario sul primario che (viceversa) non si vedono. Vediamo solo i transiti del secondario davanti e dietro al primario. La Fig. 4 mostra la visione del piano equatoriale dell’orbita  dei due oggetti.

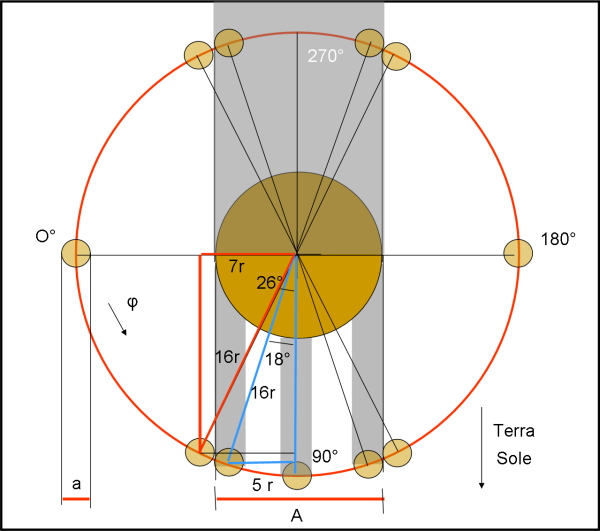
Essa ci permette di calcolare graficamente (ma anche analiticamente, ovviamente) la durata del minimo principale e del secondario, che sono perfettamente uguali. Per trovare la semidurata del minimo basta ricavare l’arcoseno di 7r/16r  (triangolo rosso) e si trova l’angolo tra l’inizio e il punto di mezzo del minimo, ossia 26°.  Se poniamo come inizio della fase rotazionale (il periodo orbitale è posto uguale a 360°) il centro del massimo di luce (φ = 0°), l’inizio del minimo avverrà a  φ = 90° – 26° = 64°.  Gli angoli di fase rotazionale dell’ingresso e dell’entrata completa  sono perciò 64 ° e 72° (dalla Fig. 4, si vede benissimo che l’entrata completa si riferisce a un angolo di 90° – 18° = 72° , dove 18° è l’arcoseno di 5r/16r come mostra il triangolo blu).

Per disegnare la curva di luce completa (differenza di magnitudine in funzione della fase rotazionale) è necessario calcolare le aree coinvolte durante la rivoluzione completa del secondario.

Quali sono le aree coinvolte? Beh… è banale, ma usiamo per comodità la Fig. 5 che rappresenta il piano perpendicolare alla linea di vista, su cui si proiettano i dischi del primario del secondario.

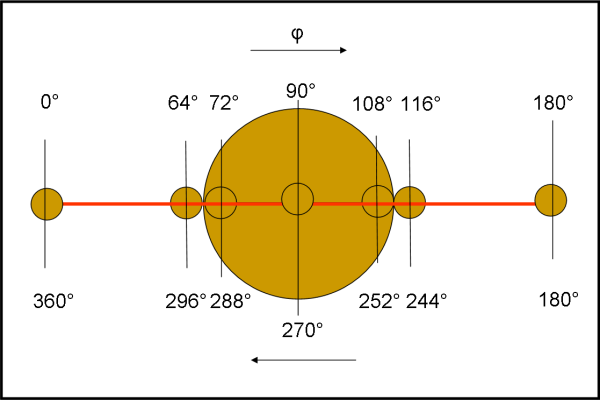
Quando il secondario è lontano dal transito l’area totale vista da terra è:

A(primario) + a(secondario)

Nel nostro caso:

R² + r² = 36 + 1 = 37

Quando il secondario è completamente davanti o dietro il primario, l’area visibile è soltanto A.

Il minimo ha quindi una profondità, espressa in magnitudini di:

Δm = - 2.5 log A/(A + a) = - 2.5 log 36/37 = 0.030 mag

E’ interessante notare la parte che contraddistingue la discesa verso il minimo. Essa è ovviamente una funzione di φ e rappresenta la parte di area del secondario che rimane esterna al bordo del primario (lo vediamo in Fig. 6).

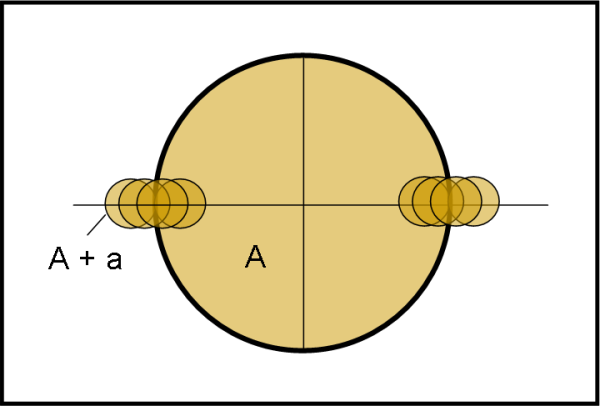
Non c’è sicuramente bisogno di calcolarla e si può tranquillamente disegnarla come un tratto rettilineo.

Il transito del secondario  davanti al primario e il viceversa hanno la stessa durata e causano la stessa perdita di luminosità, come mostra la Fig. 7.

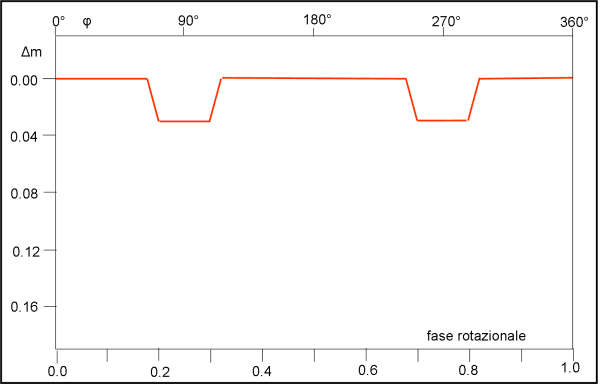
Ovviamente è un caso estremamente peculiare, ma non sarebbe molto difficile applicarlo a due ellissoidi. La curva di luce prenderebbe una più accettabile forma sinusoidale, ma senza grandi cambiamenti concettuali. Possiamo, perciò proseguire con il caso più semplice.

continua...

N.B.: La prossima volta affronteremo anche l'effetto delle ombre e invito i più volenterosi a ricavare la trasformazione della curva di luce, per un angolo di fase α uguale a 20°.

 

QUI tutti gli articoli finora pubblicati della serie "I miei amici asteroidi"