Soluzione del quiz che mise in crisi Einstein

18/03/19

Soluzione del quiz che mise in crisi Einstein

Categorie: Fisica classica Tags: Scritto da: Maurizio Bernardi Commenti:7

Einstein ...Quiz per Einstein? Ma che sarà mai?  Dai, conoscendo la velocità media totale da ottenere, oltre alla velocità media del primo tratto, si tira fuori la velocità media del secondo tratto, no?

Questi Geni, ti inventano le teorie più astruse (con tutto il rispetto eh...) piene di cose strampalate come tensori energia-impulso, spazi a 4 dimensioni, gemelli che vanno in pensione precocemente, nonostante la Fornero, e muoni che arrivano vivi per terra  e poi vanno in crisi sulle cose pratiche, che anche un bambino...

Niente di più facile:

la velocità media su tutto il percorso è la media delle due velocità (percorsi uguali) e basta fare due conti così:

chiamo x la velocità nel secondo tratto di un Km e Vm la velocità media di 30 Km/h.

Vm =  (15+x)/2 = 30      da cui ricavo subito  x = 45 (km/h)

Guarda, faccio anche la "prova".   Nooo...... se faccio la prova e calcolo il rapporto tra la somma delle distanze e la somma dei tempi, che dovrebbe essere proprio la velocità media, i conti non tornano! Infatti...

spazio totale = 1 +1 = 2 Km

tempo impiegato per il primo Km   t1 = 1/15 di ora

tempo impiegato per il secondo km  t2 = 1/45 di ora

velocità media = (s1+s2)/(t1+t2)  = 2/ (1/15 +1/45)   =  2/4/45 = 90/4 = 22,5  Km/h    che non è affatto uguale a 30 Km/h.

Oh Cielo !

Un momento, un momento...

Se il primo Km è percorso a 15 km/ora,  per arrivare in cima alla collina  occorre 1/15 di ora.

Ma se  il tragitto totale di 2 Km  va percorso a 30 km/ora, questo  significa che  tutta la strada va percorsa in  1/15 di ora.

Quindi nel preciso momento in cui si arriva  in cima.... non c'è più tempo disponibile.  L'auto dovrebbe scendere a velocità infinita per fare il Km finale in un  tempo nullo.
Il che è, ovviamente, impossibile. Quindi la RISPOSTA CORRETTA è che, date queste ipotesi,  l'auto non potrà in nessun caso percorrere i 2 km ad una velocità media di 30 km/h.
Proviamo a vedere la cosa graficamente, chissà mai che non aiuti.   Ecco, un pezzo di carta e una biro....
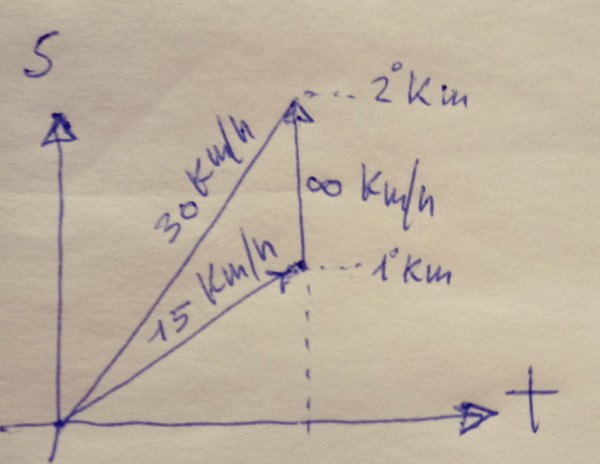
Einstein velocità auto in discesa (1)

La pendenza delle rette rappresenta la velocità.

Raddoppiando sia la velocità (da 15 a 30 km/h), sia lo spazio (da 1 a 2 km) il tempo di percorrenza non cambia.
Quindi il tempo totale dovrebbe coincidere con il tempo parziale per il primo Km.  Allora il secondo km deve essere  percorso nel tempo residuo che è zero.
Sul grafico passo da Km1 a Km2 in un tempo zero con una  pendenza verticale, che rappresenta la velocità nel secondo tratto, e significa  velocità infinita.
Adesso facciamo la prova, come prima:
velocità media = (s1+s2)/(t1+t2)  = 2/ (1/15 +0)   =  2/1/15 = 30     Questa volta, fortunatamente il risultato è giusto
Ma cosa c'è mai di subdolo nel quiz, da indurre in errore? Questa è la vera domanda a cui rispondere.
Sembrerebbe che nel vedere  i due percorsi uguali si venga indotti istintivamente  a fare la media delle velocità "sulla distanza" e non" sul tempo" , come invece deve essere.
Ovviamente, se per un determinato tempo, vado ad una certa velocità  V1  e poi, per il medesimo tempo vado ad una diversa velocità  V2 , per ogni istante del primo intervallo percorso a V1, esiste un corrispondente istante del secondo intervallo, percorso a V2, quindi la velocità media è proprio metà della somma delle due velocità.
Il ragionamento, invece, non regge riferendosi alle distanze percorse: se per un Km vado ad una certa velocità e per il successivo Km vado ad una diversa velocità, la velocità media non la ottengo sommando le due velocità e dividendo per due, a causa del fatto che non sono andato per lo stesso tempo alla velocità V1 e alla velocità V2.
La trappola "psicologica" sta nel proporre nel testo del quesito due distanze, (oltretutto uguali) "spingendo" a calcolare la media delle velocità sulla dimensione spazio invece che sulla dimensione tempo
Ma adesso  rivediamo tutto in termini generali, senza inserire i valori numerici.

Le premesse :

s_{1}=s_{2}=s              T_{1}=\frac{s_{1}}{v_{1}}

Il calcolo:

V_{m}= \frac{s_{1}+s_{2}}{t_{1}+t_{2}}   = \frac{2s}{\frac{s_{1}}{v_{1}}+t_{2}}     da cui       t_{2}v_{m} + s_{1}\frac{v_{m}}{v_{1}}=2s  ;    da cui , essendo S1 = S ,    ricavo       t_{2}=\frac{2s-s\frac{v_{m}}{v_{1}}}{v_{m}}      =\frac{s{\color{Red} (2-\frac{v_{m}}{v_{1}})}}{v_{m}}

cosa ne possiamo concludere?

La cosa più  interessante è che l'espressione tra parentesi, (in rosso) che nel nostro caso si azzera per il fatto che Vm = 2V1, con la conseguenza che, essendo nullo il tempo T2,  la V2 diventa infinita,  suggerisce anche che, nel caso di Vm > 2 V1 , il tempo T2 diventerebbe negativo.
Quindi, non bastando neppure una velocità infinita nella discesa, per ottenere la velocità media richiesta, occorrerebbe percorrere l'ultimo chilometro andando contemporaneamente indietro nel tempo.
La velocità negativa ci dice: avanti nello spazio e indietro nel tempo, che è (forse?)  diverso da dire:  avanti nel tempo e indietro nello spazio. Oppure no?
Ma a quest'ultima domanda potrebbe rispondere solo Einstein.
 
P.S. 1
Ragionando sulla velocità media e sulla media delle velocità (per chi ha calcolato  V discesa= 45 Km/h)
Vm = \frac{spazio.totale}{tempo. totale } = \frac{s1+s2}{t1+t2} = \frac{s1}{t1+t2}+\frac{s2}{t1+t2}            i due termini al numeratore si possono separare mantenendo lo stesso denominatore.
Non possiamo certo separare i termini al denominatore  mantenendo lo stesso numeratore ,  perché:
\frac{s1+s2}{t1+t2} \neq \frac{s1+s2}{t1}+ \frac{s1+s2}{t2}
E neppure possiamo dire che :
\frac{s1+s2}{t1+t2} = \frac{s1}{t1} + \frac{s2}{t2 }            perché   \frac{s1}{t1}+\frac{s2}{t2}=\frac{t2s1+t1s2}{t1t2}
e neanche che :
\frac{s1+s2}{t1+t2}=\frac{1}{2}(\frac{s1}{t1}+\frac{s2}{t2})      perché        \frac{1}{2}(\frac{s1}{t1}+\frac{s2}{t2})=\frac{1}{2}(\frac{t2s1+t1s2}{t1t2})
Date queste premesse vediamo cosa succede se i percorsi sono uguali
Vm = \frac{spazio.totale}{tempo. totale } = \frac{s1+s2}{t1+t2} = \frac{s1}{t1+t2}+\frac{s2}{t1+t2}            L'ipotesi che    s1=s2 ( = s)...implica... Vm=\frac{2s}{t1+ t2}
Se s1 = s2     ma t1 è diverso da t2 ,   la velocità media non è la media delle velocità (su percorsi uguali). E' il caso di questo Quiz
Se , invece,  i tempi di percorrenza sono uguali, allora
Vm = \frac{spazio.totale}{tempo. totale } = \frac{s1+s2}{t1+t2} = \frac{s1}{t1+t2}+\frac{s2}{t1+t2}            L'ipotesi che     t1=t2 (=t) ... implica... Vm = \frac{s1+s2}{2t }     = \frac{1}{2}(v1+v2)
Se  t1 = t2....  e  s1 è diverso da s2,  la  velocità media  è proprio la media delle velocità , (su tempi uguali)
Ma questo NON è il caso del nostro Quiz
P.S.2
L'angolo del pensiero laterale (procuratevi un paio di pinze...)
Riguardo alla  suggestiva "congettura Pautasso" non datele troppo peso: secondo il suo ragionamento (?) una macchina lunga 1 km, stando ferma, coprirebbe la distanza di 1 Km in un tempo nullo, a velocità infinita. Praticamente, tutte le auto parcheggiate si muovono a velocità infinita. Ma mi facci il piacere...
La prima ipotesi formulata da Fabrizio ottiene il risultato, anzi infiniti risultati, pur di mantenere la velocità in salita sopra i 15 Km/h e arrivare così in cima con una riserva di tempo. Ma modifica il valore numerico di un vincolo esplicito, quello dei 15 Km/h.  Si tratta di una forzatura maggiore della semplice elusione di un vincolo labile, non definito, quindi assegnabile arbitrariamente, come per esempio, la lunghezza della macchina.
Per fare un altro esempio: nel testo del quiz l'altitudine della cima non è definita esplicitamente. Quindi potrebbe essere un valore qualsiasi, piccolo a piacere, anche una altitudine pari alla lunghezza di Planck andrebbe bene. Formalmente sarebbe sempre una salita (poco ripida). Questo faciliterebbe anche la circolazione di veicoli lunghi 1 Km perché di fatto viaggerebbero in pianura,  percorrendo la "salita" e  anche la successiva  "discesa". Ma se l'altezza fosse stata dichiarata, allora saremmo vincolati a quel dato.
La seconda ipotesi di Fabrizio è più diabolica perché dissocia, perversamente, le premesse dalla domanda finale. In pratica non nega che la lunghezza della salita e quella della discesa sono ambedue di 1 Km,  neppure nega che in salita la velocità raggiungibile sia di 15 Km/h, semplicemente , alla domanda "A che velocità media deve viaggiare la macchina in discesa in modo da percorre l'intero tratto di 2 km con una velocità media di 30 km/h?"  risponde , tautologicamente: per scendere i due tratti (complessivamente di 2 km) alla velocità media di 30/Km/h, deve avere la velocità media di 30 Km/h. Assolutamente innegabile dal punto di vista formale, anche se di fatto elude il senso della domanda. Il fatto che Fabrizio abbia anche indicato la sequenza dei percorsi aggiunge un chiarore luciferino alla sua risposta.
P.S.3
L'angolo del pensiero pragmatico (prendete esempio!)
Come fa giustamente notare, da buon ingegnere e Uomo del Palloncino, il nostro Arturo Lorenzo: "... se ci accontentassimo di una precisione di +-100 km/h della misura della velocità v2 di discesa nel secondo tratto , "basterebbe" una velocità di discesa v2 di circa 4485 km/h per avere una velocità media sull'intero percorso di 29,9km/h :-)  Mentre il risultato tenderebbe a 30 km/h al tendere di v2 a infinito".
La proposta di Arturo implica che il tratto di 1 Km in discesa verrebbe percorso in un tempo pari a  1/4485  ore , ossia  (moltiplicando per 3600) pari a 0,8 secondi.  Questo  rappresenta il ritardo all'arrivo, essendo scaduto il tempo disponibile proprio nel momento di inizio della discesa.
Se la velocità fosse infinita il ritardo, invece, sarebbe zero.
Ma qual è il tempo minimo al di sotto del quale non si riesce più a fare alcuna misura?  Il tempo di Planck!    5,39121 * 10 -44  secondi...
Quindi, se la macchina arrivasse con questo ritardo, chi mai se ne potrebbe accorgere ?
Se il tempo di discesa ha questo valore, allora basta calcolare il rapporto tra 1 Km e il tempo di Planck (espresso in ore) e otteniamo la velocità in Km/ora che dovremo tenere in discesa per "dare l'impressione" di avere tenuto una media di 30/km/h su tutto il percorso.
Ecco:    5,39121 * 10 -44  secondi   sono   1,49756 * 10 -47  ore ,   pertanto   la velocità  vale   10 47 / 1,40756   =  0,66778 * 10 47  Km/h.
Certo, una velocità non proprio infinita, ma  molto maggiore della velocità della luce  che va a  3*108  m/s,   ossia  = 3,6* 3 *108   =  1,08 * 109   Km/h,  mentre la nostra auto  fila a 38  ordini di grandezza di più.
 P.S.4
I vincitori dell'ambito premio promesso (un bel niente) possono richiederlo inviando una mail a mamifaccilpiacere@scherzosempre.com e verrà loro consegnato istantaneamente! Praticamente a velocità infinita. Provare per credere.
La velocità media è proprio una "brutta bestia" per la matematica.
QUI un altro quiz che vi invitiamo a risolvere per vincere un bel... niente!

Articoli correlati

7 commenti

  1. leandro
    18/03/2019 at 12:42

    Non concordo con la soluzione data e rivendico senza indugi il rullo di tamburi. La mia soluzione, simile a quella data da Fabrizio,  è infatti corretta sia dal punto di vista matematico sia da quello "psicologico".

    matematico: la velocità media non è detto che debba essere quella istantanea costante;

    psicologico: nel quiz non è mai stato detto che l'auto non può tornare indietro.

    Il trucco sta nel calcolo della media che deve essere fatta sul tempo e non sullo spazio.

     

  2. Maurizio Bernardi
    18/03/2019 at 13:39

    Caro Leandro, premesso che il regolamento stabilisce che il premio è riservato SOLO a coloro che hanno dato una risposta (giusta o sbagliata è indifferente) , in quanto autore di 5 commenti hai già ricevuto il premio istantaneamente ( il suono del rullo di tamburi, che si propaga a mach 1,  ti raggiungerà con il ritardo dovuto alla tua lontananza). Sicuramente Scherzy potrà dare conferma di ciò.
    Chiarita la questione dei riconoscimenti ufficiali...
    Nella soluzione proposta da Fabrizio è chiaramente espresso l'intento ( furbesco)  di considerare solo i tratti in discesa, percorribili a 30 Km/h, per poter affermare che su "tutto il percorso" l'auto ha tenuto quella media. Niente da eccepire, una volta accettata l'impostazione.
    Nella tua soluzione, invece, arrivi alla conclusione che la velocità media, seguendo lo stesso schema (salita-discesa-risalita-ridiscesa), deve tenere in considerazione sia la velocità sui due tratti in salita , percorsi a 15 Km/ora, sia  quella sui due tratti in discesa, percorsi a 30 Km/h.
    Sommi le velocità sui quattro percorsi di 1 km e dividi per 3, spiegando (correttamente) che per fare la media delle velocità si deve tenere conto del tempo in cui si va a quelle velocità e non dello spazio che si è coperto.
    Ora, il tempo in cui si è viaggiato a 15 Km/h è complessivamente di 8 minuti , mentre il tempo in cui si è viaggiato a 30 Km/h è complessivamente di 4 minuti.
    Se per 8 minuti  ( 8/60 di ora) vado a 15 Km/h e per 4 minuti ( 4/60 di ora)  vado a 30 km/h la media sarà inferiore a 30 Km/h.
    Facendo la media pesata sui tempi si dovrebbe ottenere:

    V media = (15*8 + 30*4 ) / 12 = (120+120)/12 = 240/12 = 20 Km/h < 30 Km/h

    Quello che non ho capito fino in fondo è  perché dividi proprio per 3 , nel tuo commento che riporto di seguito...

    ok allora : sale a 15 kmh , scende a 30 kmh, risale a 15 kmh , riscende a 30 km .

    Vel media = (15+30+15+30)/3 = 30.

    Mi chiederete: perché diviso 3 ?

    Risposta : le medie si fanno sul tempo impiegato e non sullo spazio percorso.

  3. Vincenzo Zappalà
    18/03/2019 at 14:54

    E se il quiz proposto fosse stato pensato in un Universo in cui la velocità della luce è pari a 31 km/h. Avremmo applicato giustamente tutte le correzioni relativistiche? E se, nello stesso Universo, il principio di Heisenberg valesse anche per distanze di un km. Chi mai saprebbe dov'è realmente la macchina? (il chilometro è una nostra invenzione... per un altro Universo il chilometro è molto, molto, molto più piccolo....)

    Su, per favore, era solo un piccolo sberleffo in cui, dicono, sia caduto Einstein. Io dubito molto, ma chiunque resta un umano e può essere portato a dare una risposta immediata senza riflettere. In fondo, Einstein di errori ne ha fatti parecchi... malgrado tutto. Uno dei più grandi è stata la deflessione della luce che aveva trovato tale e quale a quella che si poteva ricavare tramite Newton. Fortunatamente, la prima eclissi lo ha graziato... permettendogli di correggere il valore finale.

    http://www.infinitoteatrodelcosmo.it/2016/08/20/soldner-la-relativita-generale-a-meta/

     

  4. Andrea I.
    18/03/2019 at 16:39

    In veritá la domanda, per come é posta, non da coordinate temporali ne ci dice come sia stata misurata la velocitá media del primo tragitto(ecco perché suona cosi strana, almeno a me). Ci dice solamente che l'auto ha percorso il primo km a una velocitá media di 15 km/h....questo nn significa necessariamente che questa media sia calcolata sull'auto sempre in movimento :twisted:

    Quindi la risposta corretta penso dovrebbe essere : "non c'é una risposta corretta a questa domanda"  :mrgreen:  :mrgreen:

  5. Maurizio Bernardi
    18/03/2019 at 17:23

    Caro Andrea, io penso invece che la risposta corretta sia proprio quella che hai dato tu, nel primissimo commento al quiz.

    Il tempo di percorrenza del primo Km, in salita, è in ogni caso di 4 minuti, qualsiasi siano state le peripezie dell'auto in quei 4 minuti.

    Potrebbe anche essersi fermata per un minuto con il radiatore fumante, e poi essere scivolata indietro per qualche metro,   con velocità negativa,  ripartendo.  Potrebbe avere accelerato lentamente  o repentinamente , avere proceduto a sbalzi, sussultando. Che importa? Alla fine il rapporto tra la  distanza (dalla partenza alla vetta) e il tempo trascorso è comunque la velocità media di percorrenza, e vale  15 Km/h.

    Giustamente, come scrivevi, dopo quei 4 minuti siamo fuori tempo massimo per recuperare la media di 30 Km/h su tutto il percorso.

    Questa considerazione rende superfluo proseguire alla ricerca di una velocità di recupero in discesa. Dovrebbe essere infinita per arrivare senza consumare tempo.

  6. Andrea I.
    18/03/2019 at 17:35

    Il buonsenso suggerisce quello...Ma!! Ma, come scrivevo prima, non ci sono coordinate temporali che colleghino gli eventi e le misure. La logica e l'esperienza ci fanno supporre che ci sia un continuum che effettivamente manca!(noi partiamo dal presupposto che la macchina debba completare il percorso partendo dalla prima misurazione.....ma dove sta scritto questo? :twisted: )

    L'altra cosa meravigliosa é che ci vengono date delle variabili completamente inutili per trarci in inganno ancora di piu! Adoro 'ste cose :mrgreen:

  7. Vincenzo Zappalà
    18/03/2019 at 17:55

    caro Andrea,

    concordo in pieno con Mau. L'unica risposta è: impossibile. Una velocità media è quello che è e come tale va presa. Sapendo la distanza, il tempo è uno e uno solo. Basterebbe questo per dare la risposta. Poco importa quello che si prospetta dopo: 4 minuti sono passati e qualsiasi cosa  venga prospettato, questo è un limite invalicabile!

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.