Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Ci sono più modi per costruire una sfera con la topologia quoziente. Il più semplice consiste però nel fare il quoziente di un disco. Fino adesso abbiamo fatto quozienti di quadrati e rettangoli, ma nulla ci vieta di farlo di altri sottospazi topologici. Consideriamo dunque un disco e i punti appartenenti agli estremi di una corda orizzontale. Identifichiamo i due punti come abbiamo fatto  per il segmento che viene trasformato in un cerchio. Quindi tale relazione trasforma la corda in un parallelo della sfera. Di conseguenza,se consideriamo tutte le corde orizzontali,  avremo come risultato la sfera.

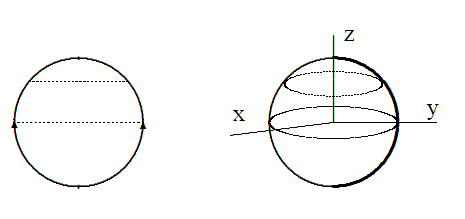
Poniamo intanto sul disco unitario 

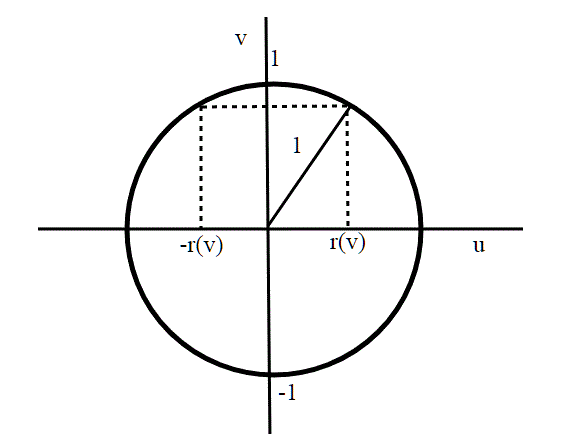
Quali sono le equivalenze non banali? Gli estremi della corda orizzontale generica di ordinata v.  Pertanto :

per ,   dove  

(per v=-1,v=1 la corda si riduce ad un punto che risulta equivalente a se stesso, corrispondente ai due poli).

La funzione parametrica f che trasforma le corde orizzontali del disco nei paralleli della sfera, è la seguente:

f:

 essendo  a denominatore.

La funzione f va dal disco che è il nostro spazio X in ; f: X--->

; se facciamo variare v nell'intervallo aperto (-1,1) otteniamo tutte le corde orizzontali del  disco; fissiamo ora un valore di v . Ciò equivale a fissare un piano z=v.  Sulla corda u varia da -r(v) e +r(v); di conseguenza l'argomento delle due funzioni seno e coseno varia da  a ;quindi i due termini che rappresentano le coordinate dell'immagine sul piano z=v, ovvero x,y sono proprio le coordinate di un cerchio di raggio r(v) che giace nel piano z=v. Al variare di v in (-1,1) otteniamo quindi tutti i paralleli della sfera.

E se (u,v)= (0,±1)? Poniamo f((0,±1)= (0, 0,±1) ovvero i poli della sfera. Questa scelta è sensata perchè la funzione così estesa è continua, come viene sempre richiesto per i nostri teoremi. Infatti se calcoliamo il limite:

concentriamoci dapprima sulla prima coordinata:

non vogliamo a questo punto affrontare i limiti di funzioni di due variabili,che richiedono varie tecniche specifiche.

Osserviamo solo che qualsiasi sia l'argomento, la funzione seno e la funzione coseno sono limitate. Il termine   tende invece a zero per v tendente a .

quindi   ma tendendo v a  tale termine va a zero. analogamente per il termine in seno. Poi chiaramente il terzo termine v tende a .  Ciò basta per concludere che:

 e quindi la funziona è continua in (0,±1) perchè assume il valore del limite.

Verifichiamo che . Sappiamo che i  punti interni al disco sono equivalenti a se stessi,quindi in tal caso l'argomento della funzione è lo stesso.  Supponiamo invece di prendere due punti sulla frontiera del disco, gli estremi di una corda.

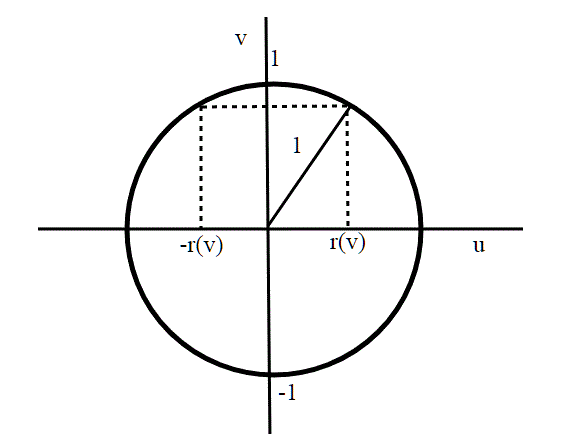
definiamo ora la nostra g([p])=f(p) ; g è ben definita, ovvero indipendente dal rappresentante della classe di equivalenza.

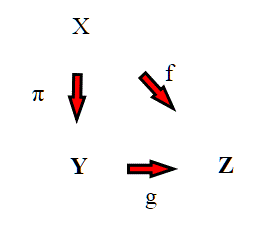
Riprendiamo l'espressione di f:

f non è iniettiva. Quali sono i punti corrispondenti della sfera  per cui f non è iniettiva? Fissiamo un valore di v diverso da che equivale a fissare un piano z=v nello spazio.

 

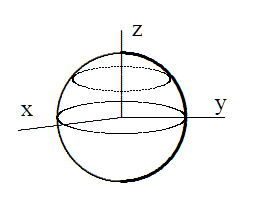
Su tale piano, avremo un cerchio di raggio r(v), al variare dell argomento da  a . Quali sono su tale cerchio gli unici punti coincidenti con coordinate diverse?  Quelli che si ottengono per valori dell'argomento  ,  ovvero per u=-r(v), u=r(v). Quindi i punti coincidenti sono quelli con  coordinate  e corrispondono alla saldatura dei due estremi della corda. Guarda caso, questi sono proprio i punti equivalenti,  . Quindi anche  se f non è iniettiva, g essendo definita come g([p])=f(p) lo è.

 

Come visto più volte, grazie al teorema necessario: possiamo affermare che g è un omeomorfismo fra la nostra sfera topologica definita come quoziente del  disco e la sfera di equazione parametrica f.