Dopo aver studiato la parte più semplice, quella relativa ai transiti tra asteroide e il suo satellite, introduciamo anche le ombre relative e la faccenda si complica non poco pur rimanendo su un caso veramente elementare.

Se non avete letto la prima parte, potete farlo QUI prima di proseguire

 

(2) Le ombre entrano in gioco

Prima di iniziare a studiare il gioco delle ombre tra satellite e corpo principale, dobbiamo tenere in conto che il primario mostra esso stesso una parte in ombra, proprio a causa di un angolo di fase diverso da zero. L’effetto non è certo evidente come nelle fasi lunari, ma è comunque un qualcosa capace di ridurre la luminosità apparente. In poche parole il disco circolare non è più tale. La Fig. 8 mostra la configurazione geometrica con un angolo di fase di 20°.

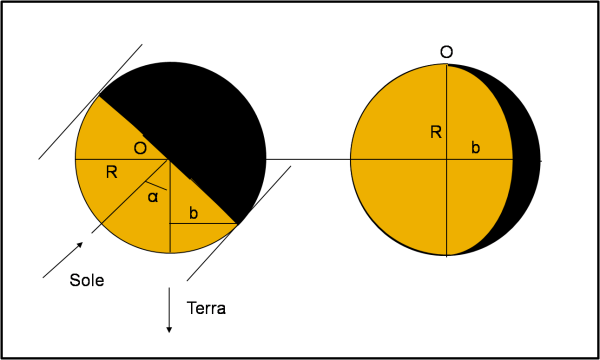
Nel lato destro del primario si nota una bella falcetta nera. Non è difficile passare dall’area nel caso di fase uguale a zero, A, a quella di fase uguale a 20°, A(20).  L’area totale apparente del primario è data da un semicerchio di raggio R = 6 e da una semiellissi che ha come semiasse maggiore sempre 6, ma come semiasse minore b = 6 cos (20°) = 5.64. Ne segue che l’area totale del primario vale:

A(20) = π(R² + R b)/2 = π(36 + 33.8)/2 = π 34.92

L’area precedente, a fase α = 0°, era, ovviamente, π 36.

Per essere precisi dovremmo anche ridurre l’area del satellite nello stesso modo fatto per il fratello maggiore…

a(20) = π(1 + 0.94)/2 = π 0.97

Dopo di che si può calcolare facilmente la differenze di magnitudine che ci si aspetta al massimo di luce influenzato dalla fase di 20° rispetto al caso di fase 0°.

Il livello del massimo di luce, passa da A + a  ad A(20) + a(20).

Ne segue che:

A(20) + a(20) = π (34.92 + 0.97) = π 35.89

A + a = π 37     (come già calcolato precedentemente)

Δm = - 2.5 log (35.89/37) =  0.033 mag

Quanto fatto ci dice solo che il massimo di luce nel caso di fase uguale a 20° è  meno luminoso, di 0.033 mag, rispetto a quello relativo al caso di fase nulla.  Questo “banale” calcolo è stato fatto solo per una completa ed elementare analisi del modello, senza, per adesso modificare sostanzialmente la curva di luce. Vi è stata solo una diminuzione di luminosità massima dell’oggetto planetario. Beh… è ovvio che la magnitudine totale aumenti con l’angolo di fase (e ciò capita, ovviamente, anche per oggetti singoli, dando luogo alla ben nota curva di fase, la cui pendenza dipende molto dalla composizione superficiale dell’asteroide).  In realtà, però, a noi interessa come l’ombra del secondario si diverta con la faccia illuminata del primario.

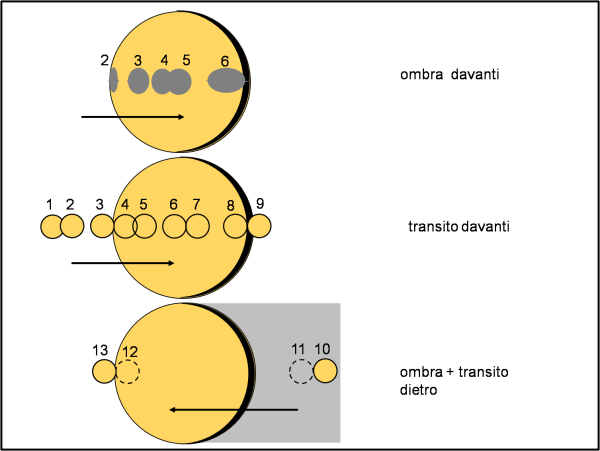
Rimettiamoci nel piano equatoriale e iniziamo a giocare con le ombre e con  transiti, in Fig.  9. Non abbiamo disegnato la parte in ombra del satellite, data la sua estrema piccolezza, ma sappiamo che lui ha sempre un’area apparente uguale a π 0.97.

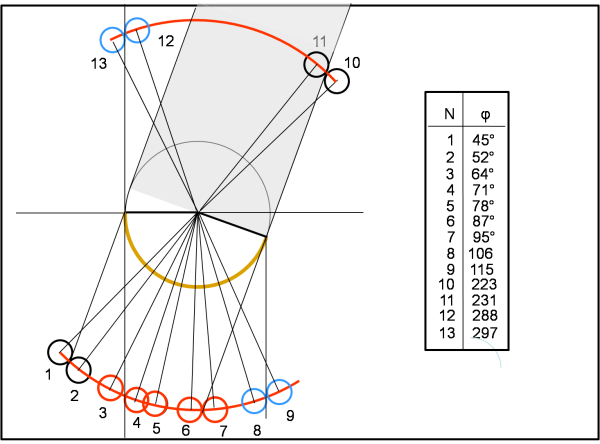
Per cercare di essere più semplici possibili e per evitare calcoli troppo noiosi, facciamo uso soprattutto di misure prese direttamente sulla Fig. 9 (gli angoli si ricavano come arctan o arcsin di rapporti di segmenti). Indichiamo chiaramente tutti i punti fondamentali per costruire la curva di luce, sia per quanto riguarda l’ombra che il transito. I dischetti neri si riferiscono a configurazioni in cui giocano solo le ombre proiettate o dal secondario o dal primario. I dischetti rossi sono quelli che si riferiscono a situazioni in cui giocano sia le ombre proiettate che i transiti. Infine, i dischetti azzurri si riferiscono a configurazioni in cui sono coinvolti solo i transiti. Sul lato destro della figura sono riportati tutti i punti “importanti” con il loro valore corrispondente dell’angolo rotazionale φ.

A questo punto dobbiamo calcolare l’area apparente vista dalla Terra rispetto a quella A(20) + a(20), corrispondente al massimo di luce. Chiamiamo ao(i) l’area dell’ombra del secondario proiettata sul primario, dove i si riferisce al punto corrispondente.

Essi sono teoricamente ottenibili dall’intersezione di un cilindro con un sfera. Senza entrare nel sottile, ci troveremmo di fronte a delle quartiche. Cerchiamo di essere seri… ciò che si vuole ottenere è soltanto la forma approssimativa di una curva di luce che, anche se fosse dominata dalla presenza di un satellite, resta sempre in balia di forme non sferiche e di macchie di albedo. Non sembra quindi proprio il caso di fare calcoli troppo sofisticati. Basta e avanza trattare l’ombra proiettata come un'ellissi che abbia come semiasse verticale sempre il valore 1, mentre quello orizzontale sia variabile, ma calcolabile facilmente dalla Fig. 10 (a sinistra)

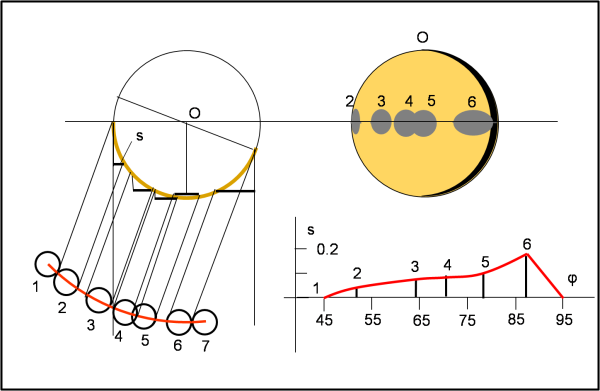
I pochi punti che abbiamo scelto sono più che sufficienti per ottenere un andamento accettabile per i nostri scopi. La curva del semiasse variabile s, in funzione dell’angolo di fase rotazionale è riportato in rosso nella Fig. 10 (a destra). L’area dell’ellissi ao(i) è proprio data da π 1 s_i.

Dobbiamo anche tener conto che quando il secondario transita davanti al primario non solo scompare l’area che mostrava fuori eclissi, ma che la sua parte in ombra nasconde una parte del primario pari alla sua falcetta scura dovuta alla fase, come mostra la Fig. 11.

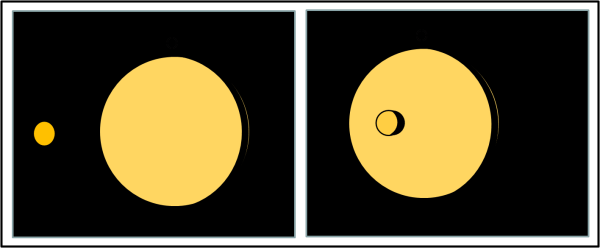
Piccola cosa, ma pari a π 0.03. Infatti l’ area visibile è π 0.97, da cui la falcetta scura è pari a π 0.03. Chiamiamola af (non datemi del pignolo, ma vale la pena tenerne conto pensando a satelliti di ben altra grandezza, anche se nel nostro caso potevamo sicuramente farne a meno).

La Fig. 12 riassume transiti ed eclissi (trascurando la falcetta  scura del secondario).

Scriviamo i valori dell’area vista dalla Terra per ogni punto fondamentale (trascuriamo il π)

1              A(20) + a(20)                =   35.89

2              A(20) + a(20) – ao(2)   =   35.89 - 0.43

3              A(20) + a(20) – ao(3)   =   35.89 - 0.75

4              A(20) – af - ao(4)         =   34.92  - 0.03 – 0.89

5              A(20) – af - ao(5)         =   34.92 – 0.03 – 1.00

6              A(20) – af - ao(6)         =   34.92 – 0.03 – 1.60

7              A(20) – af                     =   34.92 – 0.03

8              A(20) – af                     =   34.92 – 0.03

9              A(20) + a(20)                =  35.89

10            A(20) + a(20)                =  35.89

11            A(20)                             =  34.92

12            A(20)                             =  34.92

13            A(20) + a(20)                =  35.89

Ora abbiamo tutto per calcolare la differenza di magnitudine rispetto al massimo di luce nel caso di un angolo di fase uguale a 20°. Basta fare il rapporto tra l'area massima  e l'area A_app vista dalla Terra  con la solita formula

Δm = - 2.5 log (A_app/A_max) per ogni punto fondamentale precedente:

 

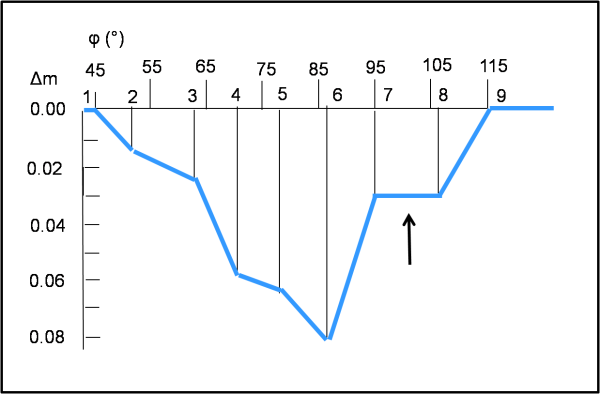
Δm₀ = 0.0

Δm₁ = 0.0

Δm₂ = 0.013

Δm₃ = 0.023

Δm₄ = 0.059

Δm₅ = 0.062

Δm₆ = 0.081

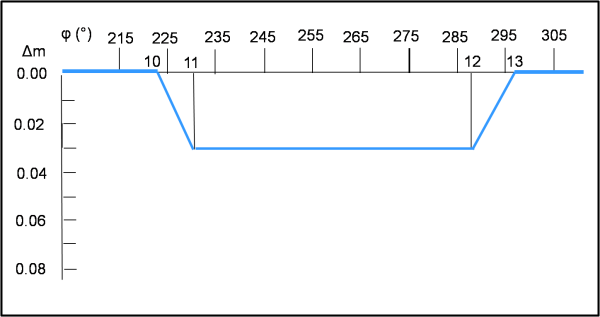
Δm₇ = 0.030

Δm₈ = 0.030

Δm₉ = 0.0

Δm₁₀ = 0.0

Δm₁₁  = 0.030

Δm₁₂ = 0.030

Δm₁₃ = 0.0

In Fig. 13 riportiamo il minimo principale e in Fig. 14 quello secondario (che risulta molto lungo e piatto).

 

Confrontiamo quanto fitto finora con la Fig. 15, quella pubblicata  con  mezzi un po’ meno artigianali nel lontano 1980.  A parte qualche angolo da smussare i risultati sono in buon accordo.

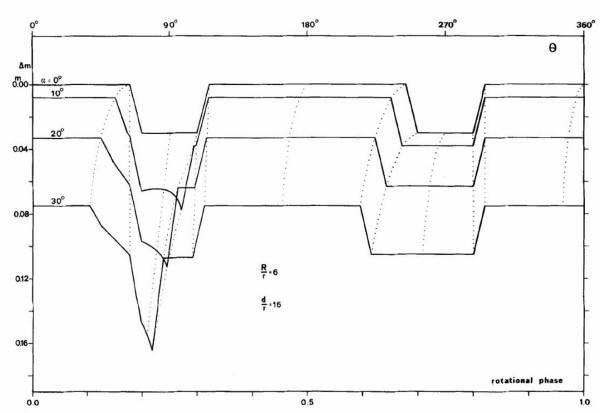
Ma ancora più interessante è la Fig. 16, dove il modello è stato applicato a due casi reali: 192 Nausikaa e 5 Astraea.

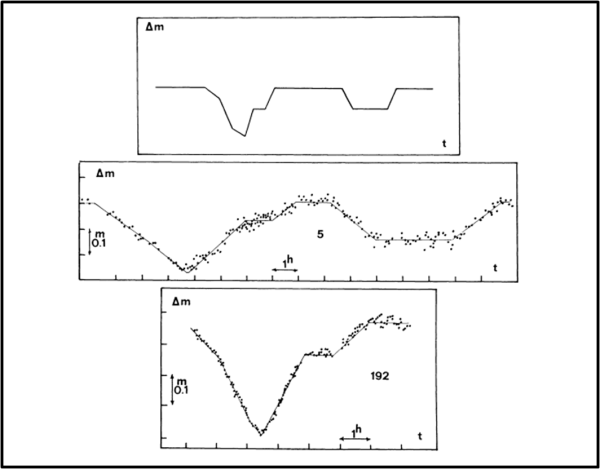
Beh… qualche dubbio potevano anche farli venire… a tal punto che molti anni dopo, qualcuno aveva pensato bene di fare guardare Nausikaa nientemeno che da Hubble oltre che al gigante del Mauna Kea. Il risultato è stato negativo, ma non era comunque facile individuare l’ipotetico satellite… Poi, la scoperta è diventata di routine, ma lasciatemi credere che la spinta iniziale sia proprio venuta da questo banale modello, un gioco per gli amanti della geometria.

E poi chissà che non esista davvero il piccolo Nausikaa b!

L’articolo originario del 1979 si può ancora trovare QUI, insieme a molte altre disquisizioni sulla formazione e osservabilità degli asteroidi doppi.

Poi, ci lanciammo nella teoria dei corpi in equilibrio formati  da “pile of rubble”, ma questa è un'altra storia...

 

QUI tutti gli articoli finora pubblicati della serie "I miei amici asteroidi"