Questo articolo fa parte della serie "La Relatività Ristretta per tutti"

Questo breve articolo vuole essere una ulteriore possibile semplificazione dei concetti espressi nel quarto capitolo. Ringrazio Leandro per avermici fatto pensare... Eliminiamo zig zag vari e limitiamoci a una descrizione qualitativa, che potrebbe dare lo scatto necessario per il passo successivo. Più semplice di così...

Questo tentativo si basa solo e soltanto sul secondo postulato di Einstein (e sulla scoperta di Vittore). Esso dice che la velocità della luce è la stessa in qualsiasi sistema di riferimento. Il che vuole anche dire che qualsiasi sia la velocità di un sistema rispetto a un altro la velocità della luce non ne viene influenzata. In parole poverissime, qualsiasi velocità si aggiunge a quella della luce il risultato finale rimane la velocità della luce.

Cominciamo con Galileo

Consideriamo la Fig. A, in cui abbiamo rappresentato una scatola che si muove in moto orizzontale (niente zig zag...).

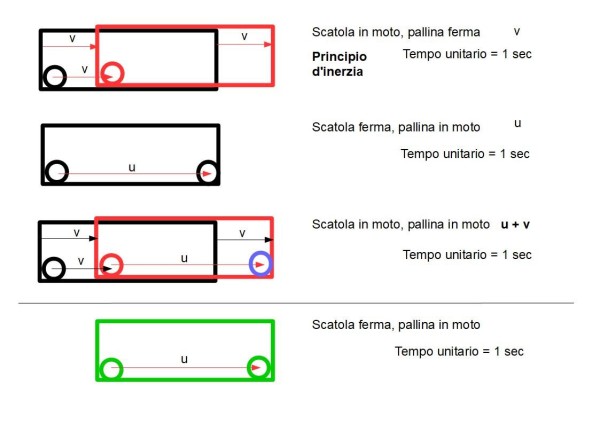
In alto vediamo la scatola nera con dentro una pallina. Immaginiamo di far muovere la scatola con una velocità v e dopo 1 secondo vediamo la situazione nella scatola colorata in rosso. Per il principio di inerzia sia la scatola che la pallina si muovono con velocità v. La scatola  si è quindi spostata verso destra in un secondo, ma la pallina è rimasta nella sua posizione iniziale, spostandosi di conserva con la scatola nella posizione rossa.

Nel disegno sottostante, immaginiamo la scatola ferma. Ci divertiamo, però, a far muovere la pallina al suo interno. Lo facciamo in modo che la pallina percorra tutta la scatola in 1 secondo. La velocità impressa alla pallina è u.

Nel terzo disegno dall'alto uniamo le due situazioni precedenti, ossia facciamo muovere contemporaneamente sia la scatola che la pallina e vediamo la situazione dopo 1 secondo. La pallina è ovviamente arrivata alla fine della scatola dato che oltre alla velocità v a cui la obbliga il principio di inerzia si è anche mossa di u. Il percorso della pallina visto dall'esterno è stato quindi quello relativo alla somma della velocità v più  u, ossia v + u.

La scatola verde, esterna al sistema della scatola in movimento, si trova già nella posizione raggiunta dalla scatola rossa dopo un secondo. La scatola verde non si è mossa, ma ha fatto muovere anche lei una pallina al suo interno con velocità u, facendola partire nello stesso istante in cui è partita quella nera. La pallina verde non potrà che vedere la pallina blu (posizione finale della pallina nera poi diventata rossa) nella sua stessa identica posizione.

Passiamo a Vittore/Einstein

La figura B è esattamente uguale alla A.

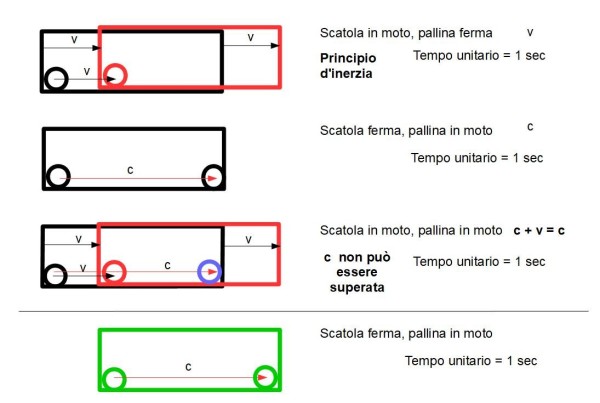
Vi è una sola piccola ed enorme differenza: la velocità u della pallina all'interno della scatola è proprio la velocità della luce c. Il postulato di Einstein ci obbliga a fare una strana somma: c + v = c. Il che vuol dire che mettendo insieme movimento v della scatola e movimento c della pallina il movimento finale della pallina deve essere soltanto c. La pallina blu, dopo un secondo, si trova più indietro della pallina verde, che ha continuato a fare quello che aveva fatto precedentemente. Questa differenza di posizione VISTA dalla scatola verde è quella che porta al tempo improprio e alla dilatazione del tempo...

P.S.: utilizzando la figura in orizzontale, però (come dice anche Leandro) bisognerebbe tenere conto anche della contrazione dell'orologio di luce e di conseguenza entra in ballo la lunghezza dell'orologio di luce, del tutto ininfluente nel caso ortogonale. Lasciatemi dire che continuo a preferire il metodo più classico, sperando, prima o poi, di inserire anche il calcolo k nell'archivio...

Questo articolo è stato inserito nella pagina d'archivio "La Relatività Ristretta per tutti" all'interno della sezione "Velocità della luce, Relatività e Buchi Neri".