Mentre mandiamo avanti il tentativo di regalare la Relatività Ristretta a tutti, ci sembra giusto riproporre articoli legati allo stesso argomento, ma di difficoltà nettamente superiore. Cominciamo con il paradosso del bacherozzo, dove la RR ha assunto risvolti veramente fisici e ha creato non poche discussioni. Questo articolo va immediatamente ad arricchire il nostro archivio dedicato alla Relatività Ristretta.

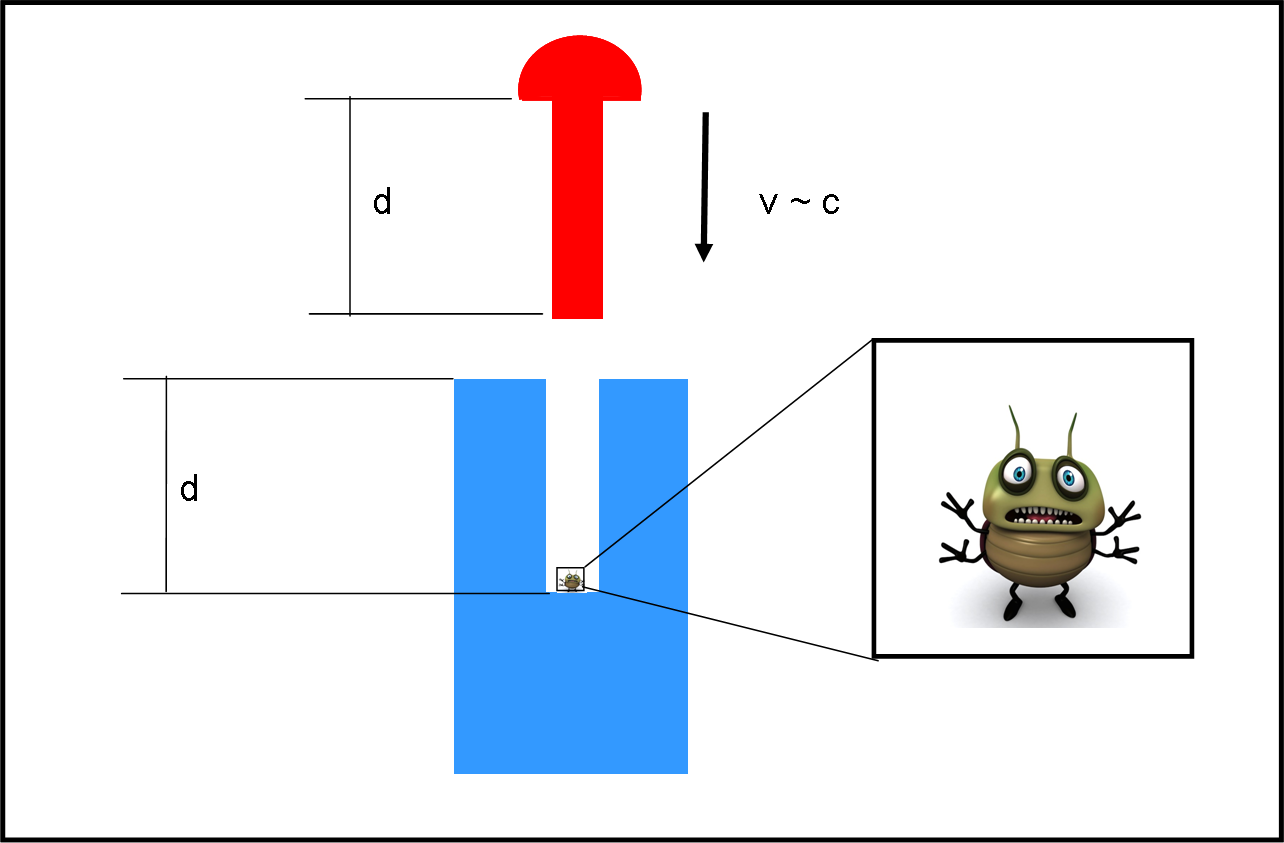
La situazione è facilmente schematizzata nella figura che segue.

Vi è un blocco di legno (o di quello che volete) con un buco al centro. Al fondo del buco si è rintanato un bacherozzo (ne vediamo un ingrandimento a lato) che si rende conto di non essere in una situazione molto tranquilla. Vi è infatti un chiodo, esattamente lungo come il buco, che sta per entrare al suo interno. Sembrerebbe che il bacherozzo abbia la sorte segnata. Tuttavia, si accorge che la velocità con cui il chiodo sta per entrare è relativistica e differisce di poco da quella della luce. In qualche modo, il bacherozzo, intravede una speranza… ma si rende anche conto che quella speranza porterebbe a un paradosso apparentemente irrisolvibile per la relatività speciale.

Il paradosso

Assumiamo che il chiodo sia più corto del buco in cui si è rifugiato il bacherozzo. Vediamo di introdurre con chiarezza il paradosso che nasce in queste condizioni.

In Fig. 1 disegniamo la situazione in cui tutto è fermo.

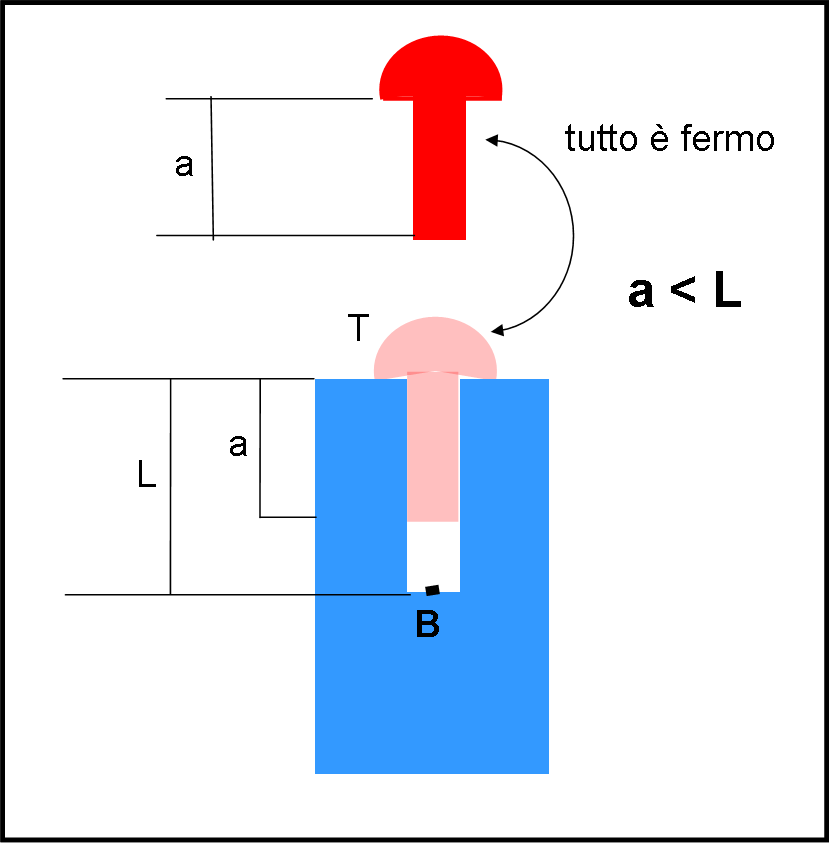
Il bacherozzo non ha nessun problema e si sente al sicuro (l’abbiamo disegnato con un piccolo trattino e indicato con B). Se il chiodo fosse inserito dentro al buco, la sua punta non lo sfiorerebbe nemmeno. Notiamo che è la posizione della testa T che determina di quanto può entrare il chiodo. In altre parole la lunghezza a (quella che interessa il bacherozzo) è la distanza tra la testa e la punta del chiodo. Non prendetemi per noioso, ma questa considerazione è molto importante. Ripetiamo ancora: è la testa che dice al chiodo di fermarsi, in quanto essa è più grande del buco.

A questo punto, entriamo nel campo della Relatività Ristretta (RR) e impartiamo al chiodo una velocità v comparabile con quella della luce c. Possiamo scrivere questa velocità come:

v = β c        …. (1)

dove β può variare tra 0 e 1. Per β = 0, v = 0 e siamo nel caso degli oggetti fermi. Per β = 1, siamo nel caso in cui il chiodo viaggerebbe alla velocità della luce (limite irraggiungibile). Possiamo perciò scrivere:

0 < β < 1     …. (2)

Qualsiasi sia la velocità del chiodo data dalla (1), con i limiti imposti dalla (2), sappiamo che la lunghezza del chiodo deve accorciarsi se visto nel riferimento del bacherozzo. In altre parole, il chiodo subisce la contrazione di Lorentz che è comandata dal celebre fattore γ, dato da:

γ = 1/√(1 – β²)

La nuova lunghezza a’ del chiodo è legata a quella in quiete a, dalla ben nota formula:

a’ = a/γ  = a √(1 – β²)

Il bacherozzo è ancora più rilassato di prima. La RR impone questo accorciamento e a lui non può che fare piacere (Fig. 2).

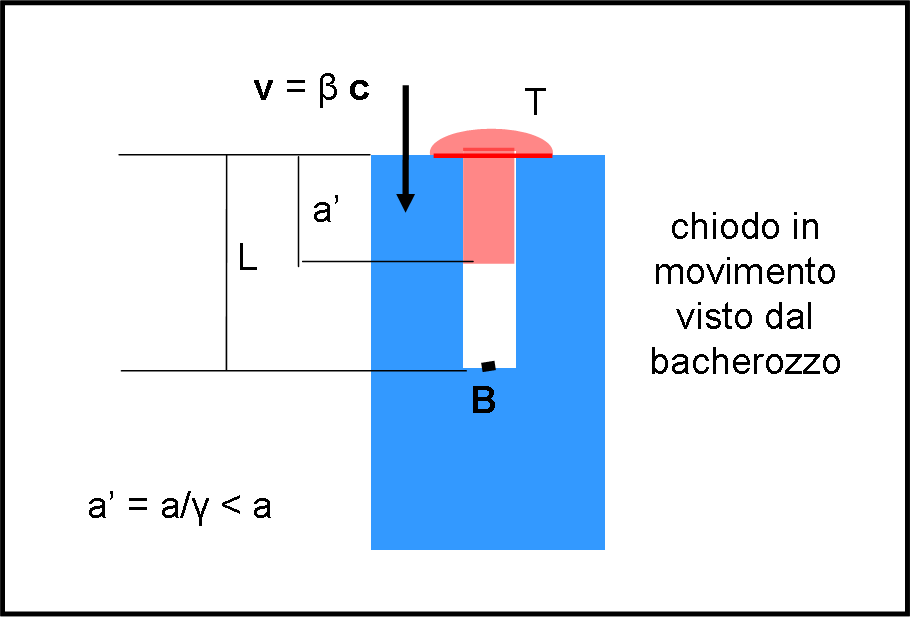
Ammettendo che la testa del chiodo “fermi” tutto il chiodo simultaneamente, il chiodo, non avendo più velocità, tornerebbe alle dimensioni che aveva quando era in quiete, comunque sempre minori del buco. Il bacherozzo non solo è salvo, ma ha apprezzato molto la RR, che gli ha mostrato una situazione ancora più favorevole. Possiamo solo dire che la testa del chiodo ha impattato il pezzo di legno a un certo istante, ma che questo fatto poco importa al bacherozzo, anzi...

ATTENZIONE: a questo punto abbiamo già accettato una caratteristica tutta da verificare. Abbiamo, infatti, considerato la lunghezza a’ come quella finale durante il moto. In altre parole abbiamo ammesso che il chiodo sia perfettamente rigido. Non spaventiamoci… ci torneremo tra poco!

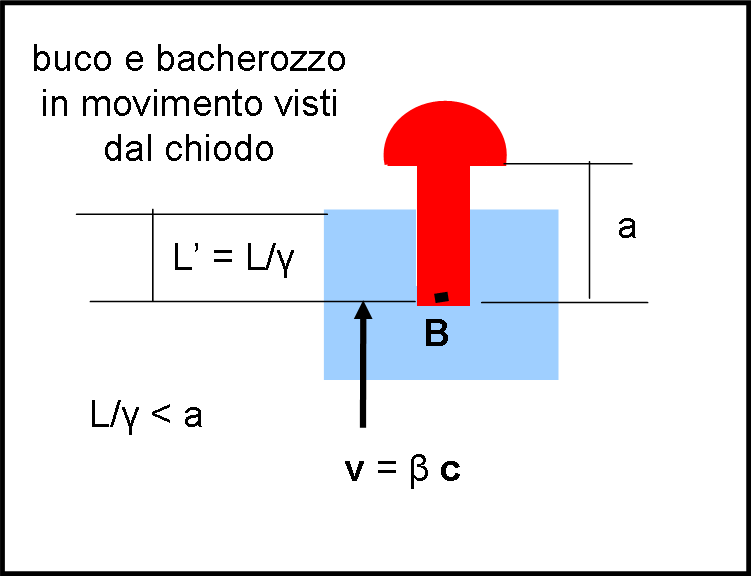
Lasciamo pure ridere il bacherozzo e cambiamo sistema di riferimento, mettendoci a cavalcioni del chiodo. Per noi le sue dimensioni sono quelle iniziali (in quiete) ed è il pezzo di legno con il buco (e il bacherozzo) che ci sta venendo incontro con velocità v = β c (stesso modulo e verso opposto a prima).

Sono quindi il pezzo di legno e il suo buco che si contraggono, ossia:

L’ = L/γ = L √(1 – β²)

Per velocità sufficientemente alte, L’ diventa più piccolo di a, ossia:

L’ <  a

In queste condizioni, il povero bacherozzo viene schiacciato, ancora prima che la testa del chiodo sia riuscita a impattare contro il pezzo di legno (Fig. 3). Anzi, sembrerebbe proprio che la testa del chiodo stia ben lontana dal pezzo di legno.

Ricapitoliamo: per certi valori di β abbiamo visto che, secondo il sistema del chiodo, il bacherozzo viene schiacciato  prima  che la testa possa toccare il legno. Per gli stessi valori di β (in realtà, per qualsiasi valore), secondo il sistema del bacherozzo, lui non può essere schiacciato.

La Relatività Ristretta dice però che un fenomeno fisico che avviene in un sistema di riferimento inerziale deve avvenire in qualsiasi altro sistema inerziale. I nostri due sistemi (chiodo e bacherozzo) sono inerziali… ma nel secondo il bacherozzo viene schiacciato, nel primo no! Siamo arrivati al paradosso.

Esiste un corpo rigido per la RR ?

A questo punto dobbiamo analizzare con molta attenzione una conseguenza della relatività ristretta che è molto meno conosciuta o, quantomeno, non viene compresa nel suo ruolo veramente fondamentale. Essa dice che due eventi che sono simultanei in un sistema di riferimento non lo sono più in un altro sistema di riferimento. Ciò, da solo, implica che un corpo non può essere considerato perfettamente rigido. In altre parole, l’informazione non può essere simultanea, in ogni sistema di riferimento.

E questo è un fatto che può essere ben compreso pensando alla costanza e alla limitatezza della velocità della luce. Immaginiamo un corpo perfettamente rigido. Per lui ciò che avviene a un suo estremo deve essere trasmesso immediatamente all’altro estremo. Ma ciò è impossibile, in quanto l’informazione non può certo superare la velocità della luce. Ciò comporta che un oggetto in movimento, se bloccato a un suo estremo, deve continuare a muoversi fino a che l’informazione relativa all’arresto non arrivi all’altra estremità del corpo, spostandosi alla limitata velocità della luce.

In termini più fisici, un corpo perfettamente rigido deve mantenere fisse le distanze tra i suoi atomi. Tuttavia, se noi diamo un colpetto a una sua estremità, l’informazione dovrebbe propagarsi istantaneamente al resto del corpo imponendogli di muoversi in modo da mantenere fissa la distanza tra gli atomi. La velocità dell’informazione dovrebbe, perciò, superare quella della luce. Ipotesi, questa, che non è ammessa dalla relatività ristretta.

Riassumendo: un corpo perfettamente rigido non può essere descritto dalla relatività ristretta e, perciò, non esiste nel mondo fisico.

Se queste considerazioni non sembrano semplicissime, non c’è da preoccuparsi. Hanno fatto discutere molti professionisti, stimolandoli a far cadere l’intera RR, che ne è, però, uscita ancora più forte e… rigida di prima!

L’intero paradosso si risolve proprio valutando il ritardo di un’informazione costretta a viaggiare a una velocità uguale a c, tenendo conto che v ha un valore a lei paragonabile. In qualche modo l’informazione è costretta inseguire il corpo che continua a muoversi per riuscire, finalmente, ad avvisarlo dell’evento già avvenuto.

Di nuovo nel sistema di riferimento del bacherozzo

Il primo passo è dimostrare che lo schiacciamento può avvenire anche nel sistema di riferimento del bacherozzo, malgrado lui si consideri salvo per qualsiasi valore di β. Il suo problema è che non ha tenuto conto della NON rigidità del chiodo…

Riprendiamo in mano quanto mostrato nella Fig. 2. Ciò che sicuramente capita per primo è l’urto tra la testa del chiodo e il pezzo di legno. Tuttavia, il resto del chiodo continua a muoversi alla stessa velocità v = βc. Nessuno lo ha ancora avvisato dell’avvenuto scontro della testa. Fondamentale è che l’informazione arrivi alla punta del chiodo e la immobilizzi prima che essa tocchi il bacherozzo.  Vi è una corsa a due tra la punta del chiodo che si muove con v = βc e l’informazione necessaria a fermarlo, che viaggia con velocità c.

Qual è il tempo necessario affinché l’informazione arrivi alla punta?

T₁ = spazio percorso/velocità

Lo spazio da percorrere è la lunghezza contratta a’, mentre la velocità è c – v (l’informazione viaggia con c, ma il chiodo gli scappa in avanti con v). Ne segue:

T₁ = a’/(c – v) = a/(γc (1 – β))           …. (3)

T₁ è il tempo necessario a fermare la punta del chiodo dopo che la testa ha impattato contro l’esterno del buco. Il povero bacherozzo deve sperare che non sia sufficiente a farla arrivare fino a lui. Qual è il valore limite per la sua vita o la sua morte? Non gli resta che considerare quanto spazio ha percorso la punta del chiodo durante il tempo T₁. Chiamiamo D₁ questo spazio.

La punta ha sempre viaggiato a velocità v, per cui:

v = D₁/T₁   e, ancora:

D₁ = v T₁        …. (4)

Il bacherozzo viene schiacciato se:

D1 > L – a’ = L – a/γ

Sostituendo il valore di D1 della (4)

Si ha:

v T1 > L – a/γ

Ricordando la (3), abbiamo:

va/(γc (1 – β)) = βca/(γc (1 – β)) = βa/(γ(1 – β))

e, quindi:

βa/(γ(1 – β)) > L – a/γ

βa/(γ(1 – β)) + a/γ > L

a/γ ((β/(1 – β) + 1) > L

a/γ ((β + 1 – β)/(1 – β)) = a ∙1/(γ(1 – β)) > L       …. (5)

Prima di proseguire, scriviamo in altro modo la quantità 1/(γ(1 – β)), ricordando che 1/γ = √(1 – β²):

1/(γ(1 – β)) = √(1 – β²)/(1 – β) = √(1 + β) √(1 – β)/(√(1 – β) √(1 – β)) = √((1 + β)/(1 – β))            …. (6)

Ritorniamo alla (5), sostituendo quanto trovato nella (6):

a√((1 + β)/(1 – β))  > L

a/L > √((1 - β)/(1 + β))

(a/L)² > (1 - β)/(1 + β)                     …. (7)

Dobbiamo proseguire, in quanto a noi interessa sapere il valore minimo di β, per il quale il bacherozzo viene sicuramente schiacciato. In altre parole, dobbiamo ricavare β dalla relazione precedente.

Per semplificare i passaggi, poniamo (a/L)² = R. Questo è un parametro molto interessante in quanto a/L non è altro che il rapporto tra la profondità del buco e la lunghezza del chiodo, proprio le condizioni di partenza.

R > (1 - β)/(1 + β)

R + R β > 1 – β

β(1 + R)  > 1 – R

β > (1 – R)/(1 + R) = (1 - (a/L)²)/( 1+ (a/L)²)       …. (8)

Il secondo membro è il valore minimo di β (β_min) per cui il bacherozzo viene schiacciato nel suo sistema di riferimento.

β_min = (1 - (a/L)²)/(1 + (a/L)²)

Sapendo che β = v/c, ricaviamo subito il valore minimo della velocità necessario per concludere l’azione in... tragedia.

v_min = c (1 - (a/L)²)/(1 + (a/L)²)

Il rapporto trovato nella (8) è sempre minore o uguale a 1 e ci dice la percentuale della velocità della luce che deve essere impressa al chiodo.

La validità fisica di quanto è stato ottenuto può facilmente essere confermata passando al limite.

Per a che tende a zero il rapporto tende a 1, ossia la v tende a quella della luce. Il chiodo non avrebbe praticamente una parte cilindrica e per giungere a schiacciare il bacherozzo lo stesso chiodo dovrebbe viaggiare alla velocità della luce, ossia la materia che può proseguire oltre al bordo del buco dovrebbe uguagliare la velocità dell’informazione. Per qualsiasi valore più piccolo, la “punta” del chiodo si fermerebbe subito ricevendo il segnale di “stop”.

Facendo, invece, il limite per a che tende a L, la velocità tenderebbe a essere nulla. Infatti, anche senza imprimergli velocità, il chiodo schiaccerebbe sempre il bacherozzo.

Notiamo, ancora una volta, che la testa del chiodo colpisce sempre il bordo del buco PRIMA che venga schiacciato il bacherozzo. Questo fatto ci conferma anche che il chiodo è ancora in movimento dopo l’urto della sua testa. In poche parole: urto della testa e schiacciamento del bacherozzo non sono eventi simultanei! Un riassunto dei vari istanti peculiari è riportato in Fig. 4.

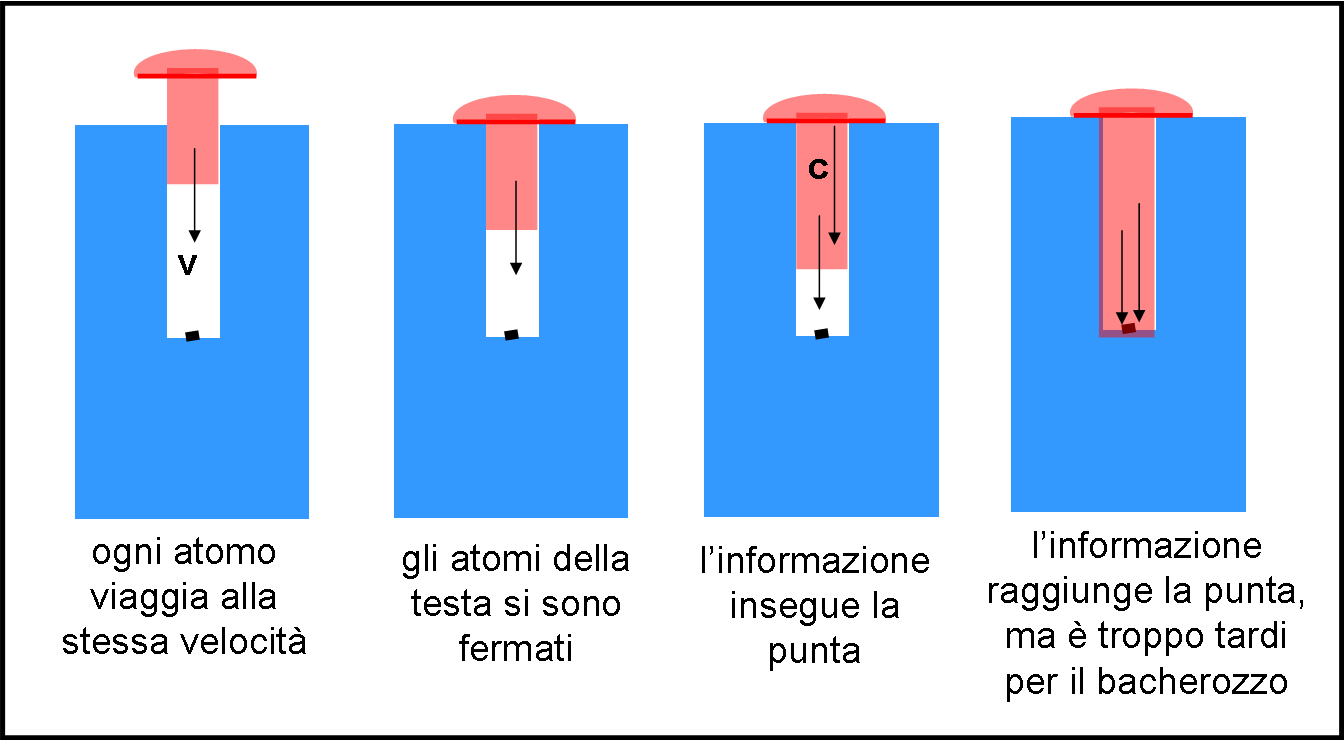
Abbiamo dimostrato che, per velocità superiori a un certo valore minimo (che dipende solo da lunghezza del chiodo e dalla profondità del buco), il bacherozzo non ha scampo.

Di nuovo nel sistema di riferimento del chiodo

Passiamo ora al sistema di riferimento del chiodo. In questo caso è il blocco di legno (con il bacherozzo) che viene verso di lui con una velocità v = β c e risulta contratto della quantità imposta dal fattore di Lorentz.

La condizione di schiacciamento del bacherozzo è immediata:

L’ = L/γ < a

Maneggiando un po’ questa relazione, si ottiene:

L√(1 – β²) < a

√(1 – β²) < a/L

1 – β² < (a/L)²

- β² < - 1 + (a/L)²

Cambiamo segno a tutti i termini e invertiamo la disuguaglianza:

β² > 1 - (a/L)²

β > √(1 - (a/L)²) = β_min2     …. (9)

Confrontiamo la (9) con la (8) e si vede subito che

β_min2 > β_min

Si ottiene un risultato che non soddisfa del tutto. E’ vero che il bacherozzo viene schiacciato, comunque, ma sembra che sia necessaria una velocità maggiore di quella che abbiamo trovato prima.

Il paradosso si risolve

Prima di trarre conclusioni avventate, analizziamo meglio la situazione, dato che in questo caso abbiamo PRIMA lo schiacciamento del bacherozzo. Ma cosa capita alla testa del chiodo? Essa non urta  contro il blocco di legno?

Per rispondere, mettiamoci nel caso in cui la contrazione del blocco di legno non è sufficiente per fare arrivare il chiodo a colpire il bacherozzo. In altre parole, la velocità non è abbastanza alta perché il buco si contragga fino allo schiacciamento del bacherozzo. Siamo nelle condizioni di Fig. 5, dove si nota benissimo che questa volta è nuovamente la testa a urtare per PRIMA il legno.

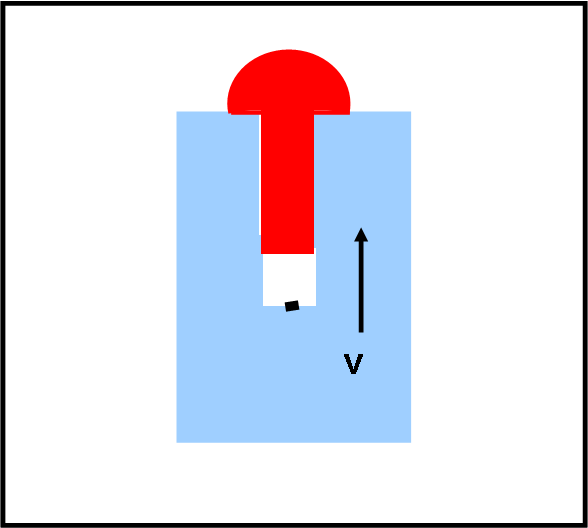
Gli atomi danno il segnale dello stop, ma il resto del buco (e con lui il bacherozzo) non lo sa ancora e continua a muoversi con velocità v = β c. Facciamo un po’ di conti…

Quanto tempo ci vuole affinché l’informazione che parte dal bordo del buco arrivi alla punta del chiodo? Semplice:

T₂ = a/c

L’informazione viaggia, infatti, alla velocità della luce.

Durante questo tempo il fondo del buco percorre una lunghezza:

D₂ = v T₂ = β c a/c = βa

Ne segue che nel sistema di riferimento del chiodo (fermo) si ha lo schiacciamento del bacherozzo se:

D2 > L/γ – a

βa > L/γ – a

a(1 + β) > L/γ

a/L > 1/(1 + β) γ)

a/L > √(1 – β²)/(1 + β)

a/L > √(1 – β)√(1 – β))/(√(1 + β)√(1 – β))

a/L > √(1 – β)/√(1 + β)

(a/L)² > (1 – β)/(1 + β)        …. (10)

Fermi tutti! Paragoniamo la (10) con la (7): sono identiche per cui è inutile svolgere i passaggi successivi. Sappiamo già che valore di β troviamo…

β_min = (1 - (a/L)²)/(1 + (a/L)²)

Accidenti! Abbiamo ritrovato la stessa velocità minima ricavata nel sistema di riferimento del bacherozzo.

Un riassunto dei vari istanti peculiari viene riportato in Fig. 6.

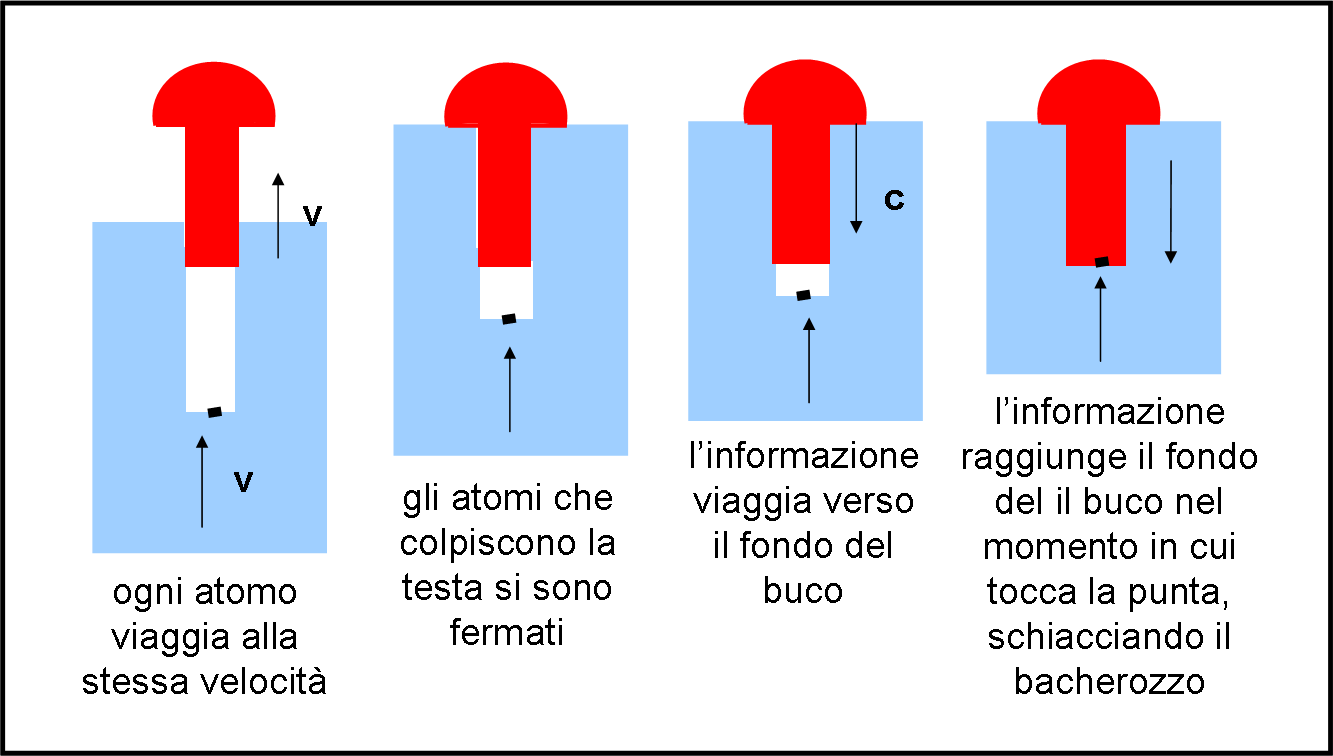
Ne segue che se si supera lo stesso valore della velocità, il bacherozzo viene schiacciato sia nel suo sistema di riferimento che in quello del chiodo.

Il paradosso è stato completamente risolto! Infatti, lo stesso identico fenomeno avviene in entrambi i sistemi di riferimento, imponendo la stessa velocità.

Analisi finale

Possiamo ancora fare alcune importantissime considerazioni.

Notiamo che in entrambi i sistemi l’urto tra la testa del chiodo e il bordo del buco avviene per PRIMO se:

β_min < β < β_min2

Infatti, se β > β_min  avviene  sicuramente per primo l'evento "urto della testa", nel sistema del bacherozzo (come abbiamo dimostrato precedentemente).

Tuttavia, sappiamo anche che se β < β_min2 non è possibile che l'evento "schiacciamento del bacherozzo" avvenga per primo, nel sistema del chiodo (come abbiamo dimostrato precedentemente) e quindi anche in questo caso abbiamo per primo l’urto della testa.

Se non capita quanto  appena detto (β > β_min2), i due sistemi, pur ammettendo che il bacherozzo venga schiacciato, differiscono nella conclusione su quale evento avvenga per primo: l’urto della testa (sistema del bacherozzo) o lo schiacciamento del bacherozzo (sistema del chiodo)

Poco male, dato che il fatto è CONSISTENTE con la Relatività Ristretta, che si basa proprio sulla relatività della simultaneità!

C’è poco da fare… dilatazione dei tempi, contrazione delle lunghezze sono ricadute molto importanti, ma nascono entrambe dalla vera base della RR: la relatività della simultaneità. Se non si comprende bene questo concetto, la RR mantiene sempre qualche lato oscuro o fa cadere, prima o poi, in confusione. Qualsiasi paradosso si può risolvere solo e soltanto considerando questo concetto base, compreso quello celeberrimo dei gemelli!

Terminiamo con una caso particolare che aiuta ancora meglio a capire queste ultime frasi.

Ammettiamo che β sia proprio uguale a β_min2. Siamo in condizioni peculiari, in quanto i due eventi sopra citati avvengono nello stesso istante nel sistema del chiodo (esso riempie perfettamente il buco nello stesso istante). Non lo sono, invece, nel sistema del bacherozzo.

Capiti perfettamente i concetti esposti in questo splendido paradosso, la maggior parte degli altri diventano giochi da ragazzi (e lo proveremo…).

P.S.: alcuni interessanti commenti si possono trovare al fondo degli articoli originali, QUI e QUI