Categorie: Senza categoria
Tags: black box combinazioni Pautasso
Scritto da: Maurizio Bernardi
Commenti:13
Soluzione del quiz: Oreste e la scatola nera
Come è facile immaginare, prima di pubblicare un quiz come questo ci si assicura di poterne proporre una soluzione ragionevole. Non sempre però si possono esplorare tutte le possibili impostazioni e avere la certezza che la soluzione sia la più efficiente e/o la più elegante.
E' successo varie volte che nei commenti emergessero impostazioni alternative più semplici di quella predisposta come soluzione “ufficiale” e questo è motivo di soddisfazione, perché sta indicare l'interesse e l'impegno dei lettori.
Proprio prima di pubblicare questo quiz ne parlavamo con Vincenzo e mi ero espresso con queste precise parole:
Non credo che si riesca a risolvere con meno di 10 misure, comunque non si sa mai, magari ci fosse un lettore che ci riesce !
Ebbene, il commento di Leandro, opportunamente elaborato, consente di arrivare a risolvere il problema con solo 9 misurazioni e con una metodologia più semplice e facile da descrivere di quella (che vi risparmio) a cui avevo pensato.
Bravo Leandro!
Ed ecco la soluzione “rivisitata”.
Prima di mettere mano al tester per eseguire le misure, costruiamo una matrice in cui le righe rappresentano le connessioni realizzate con i due conduttori posti sui contatti esterni, mentre le colonne rappresentano la distanza (più piccola) tra i due punti collegati internamente.
In ciascuna cella apparirà l'esito della lettura , ossia la risposta alla domanda “esiste la continuità?” che sarà 0 per dire SI e 1 per dire NO.
Un esempio che illustra la struttura della matrice dei collegamenti esterni e interni |
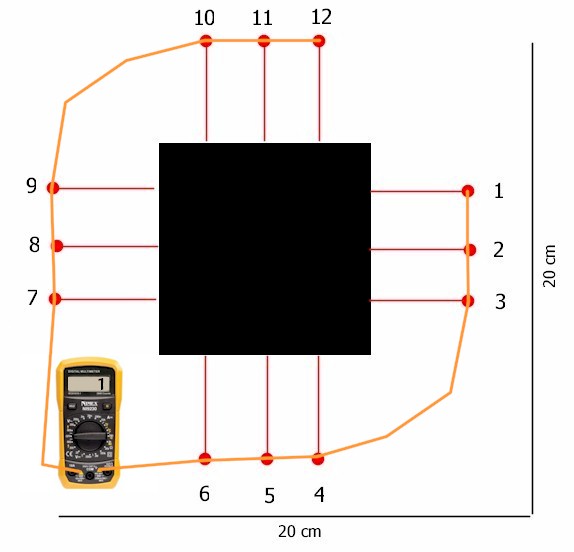
Il tester segna 1: significa che tra l'insieme dei contatti 1-6 e quello 7-12 non esiste un collegamento. ( riga 1 della matrice). Occorre verificare cosa succede facendo scorrere i punti di contatto dei due conduttori. |
Nella matrice, la colonna 1 indica che un punto è collegato direttamente al successivo, la colonna 2 indica che il punto è collegato al punto che segue il successivo, e così via fino ad avere un salto di 4 posizioni intermedie tra un punto e l'altro (es: 1 collegato con 6).
E' evidente che dopo 6 righe i valori si ripetono, per la simmetria del sistema.
Se ora eseguo fisicamente sei letture consecutive, partendo da una qualsiasi riga della matrice e spostando di volta in volta i conduttori, come opportunamente suggerisce Leandro nel suo commento, ottengo una sequenza di valori 0 e 1 in cui compare sempre almeno un valore 0.
Se nella sequenza appare un solo 0 mi troverò nel caso della prima colonna e il contatto nascosto è tra due conduttori adiacenti. Ma quali?
La riga in cui appare il valore 0 rilevato, indica il primo contatto impegnato (toccato dal primo conduttore), il successivo sarà l'altro elemento della coppia. Ma esiste anche l'alternativa offerta dal secondo conduttore, il cui primo punto di contatto potrebbe essere abbinato al successivo.
Non resta che rimuovere ambedue i conduttori ed eseguire una misura su un abbinamento: o esiste la continuità, allora quello è proprio l'accoppiamento presente, oppure non c'è continuità, e quindi l'abbinamento che interessa è l'altro.
Avremo così ottenuto la risposta con SETTE misurazioni.
Se il numero di 0 presenti nelle 6 letture è di due, ci troveremo nella colonna 2, ossia i contatti collegati internamente saranno quelli che dedurremo dalla riga che precede quella in cui appare (o ricompare) il valore 1. Anche qui basta rimuove i conduttori e eseguire la settima misura come nel caso precedente.
Allo stesso modo procederemo quando le 6 letture contengono una sequenza di 3, 4 ,5 valori 0 ottenendo il risultato nel limite di sette misurazioni.
TUTTAVIA... questa metodologia non risolve il caso in cui la sequenza delle 6 letture ci dia sistematicamente il valore 0, perché quando i punti collegati sono distanti sei posizioni, (presentandosi, per così dire, “diametralmente opposti”) il collegamento risulta sempre presente.
Facendo una radiografia della scatola nera vedremmo, ad esempio che il contatto 1 è collegato con il contatto 7, oppure il 4 è collegato con il 10, oppure il 6 con il 12 e così via.
A valle delle sei letture sembrerebbe così di doverne eseguire altre 5 per arrivare al risultato. Ma possiamo procedere più speditamente in questo modo:
Collego con il primo conduttore i punti 123 e con il secondo i punti (opposti) 789. Supponiamo nel caso più sfavorevole che questa settima misura indichi 1 ( nessun collegamento).
Inevitabilmente il collegamento esisterà tra il gruppo 456 e il gruppo 10 11 12. Non occorre fare misure per averne certezza.
Passiamo allora a collegare 45 da un lato e 10 11 dall'altro ed eseguiamo l'ottava misura
Nel caso più sfavorevole sarà 0 (fosse stata 1 avremmo avuto la certezza che l'abbinamento cercato era tra 6 e 12).
Non ci resta che verificare una delle due alternative, con la nona misurazione. Se il risultato che otterremo sarà 0 l'avremo individuata, se invece sarà 1 la risposta è data dall'altro abbinamento.
Ecco un buon risultato con solo 9 misurazioni. Qualcuno riuscirebbe a fare di meglio? Chissà...
Aggiornamento : se vi interessa sapere come va a finire la faccenda, QUI trovate l'epilogo
13 commenti
Leggo in ritardo il quiz e la soluzione, entrambi stimolanti. Sarà il caldo che ha iniziato a picchiare duro qui in Salento o una insospettata tendenza alla violazione di sistemi di sicurezza (
) ma stavo pensando ad una alternativa. Premesso che mi è parso di capire che la scatola serve a far aprire la porta, che il giocatore ne è a conoscenza e che l'apertura avviene solo quando si collegano tra loro due dei 12 contatti che escono dalla scatola nera (ma non mi pare dica che debbano essere collegati solo ed esclusivamente questi due contatti), io farei come segue. Visto che ho disponibili due spezzoni di cavo di rame nudo ciascuno lungo 50 cm e che il lato della ipotetica piastrella dentro cui può essere inscritto l'apriporta è lungo 20cm, collegherei tra loro, mediante gli spezzoni di cavo tutti e 12 i contatti, così da formare, con i cavetti, un ideale quadrato di lato 20cm passante per i 12 contatti. Mi avanzerebbero 20cm di cavo di rame. A quel punto la porta si aprirebbe inesorabilmente. Se volessi scoprire quali erano i 2 contatti tra loro collegati all'interno della scatola, mi basterebbe sollevare il cavo di rame da ciascuno dei contatti. Poiché 2 di questi sono collegati dentro la scatola, la serratura di richiuderebbe sollevando il cavetto da almeno uno dei due. A seconda da quale contatto io inizi , potrebbe capitare quello giusto al primo tentativo (una sola mossa) , oppure all'ultimo tentativo (10 mosse). E' vero, nel caso peggiore (i due contatti collegati nella scatola sono tra loro adiacenti o consecutivi) una mossa in più rispetto alla soluzione, ma in compenso non ho usato il tester 
Caro Arturo, il tuo mi sembra un nobile tentativo di sciogliere un nodo Gordiano alla maniera di Alessandro Magno oppure, più modernamente, mi ricorda la soluzione "original thinking" di Kirk del test della Kobayashi Maru ( vedi Start Trek II l'ira di Kan, 1982).
Il testo del quiz diceva così:
Solo DUE dei 12 contatti sono messi in collegamento DENTRO la scatola nera con il circuito di apertura della porta.
Per aprire si dovranno collegare questi due contatti tra loro.
La richiesta di conoscere la precisa identità di quei due contatti con un numero di tentativi minimo, implica che la serratura non funzioni semplicemente mettendo tutti i conduttori in contatto tra loro, ma (solo) collegando proprio e solo quei due contatti. Del resto, anche con il metodo suggerito da Leandro il collegamento si realizzerebbe inevitabilmente entro la sesta mossa, o addirittura entro la prima (ma coinvolgendo anche altri contatti, quindi senza conoscere in nessun caso l'identità dei due da identificare) e non per questo la serratura si aprirebbe.
Insomma la frase che hai usato: l'apertura avviene solo quando si collegano tra loro due dei 12 contatti è corretta, ma risulta ancora più chiara se scritta così: l'apertura avviene quando si collegano tra loro solo due (ben particolari) dei 12 contatti
Non è poi detto che, ammesso che la serratura si aprisse collegando tutti i contatti assieme, la riapertura del collegamento farebbe richiudere la serratura ( pensa solo agli allarmi che, una volta innescati , non si fermano più, neanche ripristinando la situazione iniziale).
A questo punto ti chiederai legittimamente come si fa a chiudere la porta
ma questa è un'altra storia...
Insomma , adopera pure il tester, ma trovaci una soluzione che permetta di individuare la risposta in meno di 9 mosse...
Mi appoggio al tuo disegno, supponendo per prima ipotesi che i contatti collegati internamente siano su cavi opposti, ovvero che la prima misura dia 0. Teniamo collegati 12.7.Consideriamo il tratto 1.6 ,; isoliamo i due contatti 1 e 6. Misuriamo con il tester; se dà 1contatto il contatto é 1 o 6. Con una misura troviamo qual e dei due. Se dà 0 é compreso fra 2.5. Isoliamo 2 e 5 e misuriamo. Se dà 1 è 2 o 5. Con una misura troviamo qual è.se dà 0 é fra 4 e 2 e con una misura troviamo qual è. Quindi al massimo tre misure. Adesso ripetiamo per 12.7 lo stesso discorso, tenendo collegati 6.1.
Quindi in tutto sei misure se non erro più quella iniziale. Se quella iniziale dà uno i contatti si trovano su uno stesso ramo . serve una misura per determinare qual e. Poi si usa una tecnica come quella sopra ottenendo un numero di misurazioni ancora minore.
Sper di aver capito bene quello che si può e quello che non si può fare. Ti dirò che all inizio avevo capito poco o niente. Per questo ho risposto adesso
Caro Umberto, la prima parte del tuo commento , quella che tratta la situazione in cui la lettura iniziale è 0, e quindi i contatti collegati si trovano rispettivamente uno su un cavo e l'altro sull'altro cavo, è ineccepibile e con un totale di 7 misure porta al risultato. Io la considero la situazione più favorevole e cercherò di provarlo.
Supponiamo allora che, alla prima misura, il risultato sia 1. in questo caso il circuito è aperto e si deduce che i due contatti si trovano o sul conduttore che unisce 1-6 oppure sull'altro, che unisce 7-12.
Come tu dici dovremo procedere analizzando dapprima un insieme, diciamo quello da 1 a 6. Recuperiamo i nostri cavi e usiamone uno per unire i contatti 1 2 3 mentre l'altro unirà 4 5 6.
Il numero totale di collegamenti possibili tra coppie di questi punti è di 15.
Supponiamo che, inserendo il tester tra i due cavi, si ottenga il valore 1 ( quindi i contatti cercati non sono su cavi opposti , ma su uno stesso cavo). Con questa misura ( la seconda) abbiamo eliminato 9 collegamenti sospetti dei 15 possibili e ora sappiamo che il collegamento ( se è in questo ambito) si trova o nella terna 123 o nella terna 456.
All'interno della terna 123 si possono formare 3 possibili coppie. Lo stesso vale per la terna 456. Dovremo studiare ambedue le terne per scoprire se in esse c'è .
Iniziamo separando da un lato 1 2 (collegati) e dall'altro 3. Con il tester eseguiamo la terza misura e supponiamo sia ancora 1. Possiamo escludere che il contatto 3 sia coinvolto. Passiamo allora alla misura numero 4: verifichiamo se i contatti sono 1 e 2. Ancora otteniamo valore 1 con il ché possiamo escludere la terna 123 e passare ad analizzare l'altra terna 456.
Occorrono altre due misure, come abbiamo appena visto, per escludere anche questa terna. Arriviamo così ad un totale parziale di 6 misure ( infruttuose) e non ci resta che concentrare l'attenzione sui contatti 7-12.
La routine si ripete come sopra. Con la misura 7 possiamo escludere 9 possibilità, poi dovremo studiare la prima terna con una ottava e con una nona misura. Lo studio della seconda terna è decisivo: se la decima misura (tra la coppia 10,11 da un lato e il contatto 12 dall'altro) sarà 1 avremo trovato che i contatti cercati sono 11 e 12, se invece, nel caso più sfavorevole, avremo che la decima lettura ci dà 0, allora dovremo eseguire la undicesima misura tra 12 e uno dei due contatti ( 10 o 11) per trovare la risposta definitiva.
Se questo, come credo, è il percorso per individuare la coppia cercata, concorderai che nel caso più sfavorevole il numero di misure necessario è di 11. Ma può darsi che il metodo a cui pensi sia un altro.
no, io intendevo che basta una misura per decidere se la coppia é in un ramo o Nell altro. Basta collegare il tester a 1.6. Se viene zero la coppia é in 1.6 altrimenti in 7.12. Dopodiché ci riduciamo a cercare su un insieme più piccolo, e senz altro il numero di tentativi é più piccolo. Ma se serve lo scrivo per esteso.
Questo è proprio il punto cruciale... una volta appurato che i due contatti si trovano in un ramo oppure nell'altro abbiamo una situazione di questo tipo: Esaminiamo il collegamento che unisce i contatti da 1 a 6.
Se non rimuovi il conduttore e misuri con il tester tra 1 e 6, troverai sempre un contatto ( tester=0) indipendentemente dal fatto che all'interno della scatola due contatti siano collegati oppure non ci sia alcun collegamento. Ecco la figura corrispondente
Questo significa che non si ottiene alcuna informazione, perché il collegamento è dato, in ogni caso, proprio dalla presenza del connettore esterno.
Se invece rimuoviamo il cavo esterno e mettiamo il tester tra 1 e 6 , troveremo la misura 1 solo nel caso che esista un contatto interno proprio tra 1 e 6, e solo in quel caso. Se invece il contatto esiste tra altri punti, esempio da 5 a 3 ( o fra 4 e 2 oppure tra 6 e 5 ... ) , è come se non esistesse alcuna connessione, e il tester segnerà sempre 1. il che non ci fornisce alcuna informazione.
scusa mau. Una volta appurato che si capisce in che ramo si trovano entrambi si spezza il ramo in due e ci si riduce al problema precedente con due cavi e tre contatti
Dopo la prima misura capisco che si trovano in uno dei due rami.
Ma quante misure occorrono per capire quale dei due?
unisco 1 punti 7-12 con un cavo e vado su un puntale del tester, poi con l'altro cavo vado sul 12 e sull'altro puntale del tester. se segna 0 la coppia si trova su 7-12 altrimenti sull'altro ramo.
ignora l ultimo commento. Devo pensarci un po' sopra ma sono convinto che questo secondo caso si possa anch esso risolvere e con meno passaggi. Scusa
Ok Umberto, prenditi tutto il tempo che ti serve, non c'è alcuna fretta. Grazie per la tua attenzione.
con i due rami separati i tentativi sono quelli che hai scritto sopra. Ho provato anche a lavorare con tre rami ma se da un punto di vista trovare la coppia su 4 punti è più facile bisogna moltiplicare per tre. Il metodo é valido ma non scende sotto i 9 tentativi. Il quiz lascia comunque degli interrogativi sul minimo numero di tentativi. Comunque interessante e fuori dalle solite storie. Torno alle tri-varietà che in fin dei conti sono più facili!
Ok Umberto , grazie e buon divertimento con le trivarietà ( che siano più facili mi sembra difficile...)