Le (poche) risposte arrivate hanno fatto subito capire che diverse sono le vie di soluzione e che molto importante è la scelta dell'origine degli assi. Proponiamo tutte e tre le risposte (compresa la mia), lasciando a voi la scelta della più elegante e immediata (anche se sembrano del tutto equivalenti)...

Soluzione di Enzo

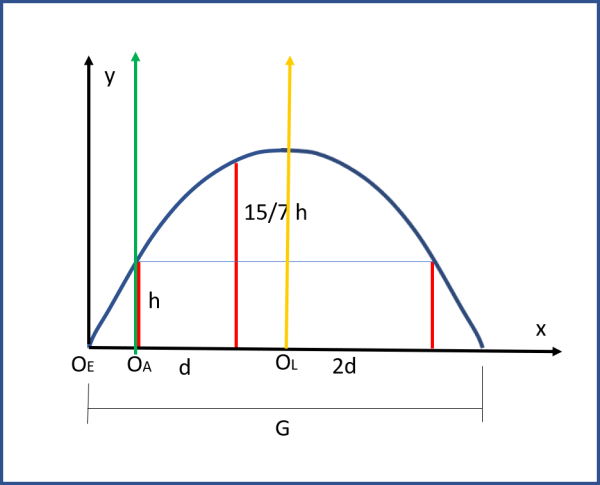
Riporto subito la figura relativa al problema, che ci servirà per tutte le risposte:

Io ho preso l'origine in O_E in modo da potere scrivere l'equazione della parabola nella forma (la concavità è verso il basso, da cui il segno meno davanti ad a):

y = - ax² + bx            .... (1)

La parabola passa per l'origine, per cui c = 0

Mi servono le coordinate di almeno due punti della parabola per scriverne l'equazione. Tuttavia, possiamo fare alcune considerazioni. La prima è quella di legare i coefficienti a e b alla gittata G.

Basta imporre y = 0 all'equazione (1)

0 = - ax² + bx = x (b - ax)

La soluzione x = 0 la conosciamo già (origine); la seconda soluzione dà proprio la gittata, ossia la distanza dall'origine del secondo punto in cui si annulla la y.

ax - b = 0

x = G = b/a

Possiamo allora scrivere l'equazione della parabola in funzione non di x , ma della gittata G. Basta dividere tutto per a e si ottiene:

y/a = - x² + G x  = x (G - x)         .... (2)

Il primo punto per cui vogliamo far passare la parabola ha ordinata h, ma qual'è la sua ascissa? E' facilissimo ricavarla dai dati del problema. Il primo e il terzo muro hanno la stessa altezza h, il che vuole dire che, per simmetria della parabola, la distanza tra l'origine e il primo muro deve essere uguale alla distanza tra il terzo muro (che ha la stessa altezza h) e il punto di caduta.

Chiamiamo x₁ questa distanza. Abbiamo:

G = x₁ + 3d + x₁

da cui:

x₁ = (G - 3d)/2

y₁ = h

Il secondo punto (secondo muro) in cui far passare la parabola ha un ascissa pari a x1 + d (dato del problema), perciò:

x₂ = x₁ + d =  (G - 3d)/2 + d = (G - 3d +2d)/2 = (G - d)/2

y₂ = (15/7)h

Inserendo i due punti così determinati nell'equazione della parabola (2), si ottiene il sistema

h/a =  x₁(G - x₁) = (G - 3d) (2G - G + 3d)/4 = (G - 3d)(G +3d)/4 =  (G² - 9 d²)/4

(15/7)(h/a) =   x₂ (G - x₂) = (G - d) (2G + d - G)/4 = (G² - d²)/4

Moltiplichiamo entrambe le equazioni per 4 e otteniamo:

4h/a = G² - 9d²

(15/7)(4h/a) = G² - d²

Moltiplichiamo la seconda  per 7/15

4h/a = G² - 9d²

4h/a = 7(G² - d²)/15

Essendo uguali i primi membri devono esserlo anche i secondi, per cui:

G² - 9d²  = (7G² -7d²)/15

15 G² - 135 d² = 7G² - 7d²

8 G² = 128 d²

G² = 16 d²

G = 4d

Risultato del tutto indipendente da h.

Soluzione di Leandro

Se spostiamo gli assi cartesiani in modo che l'asse y passi per il vertice della parabola, la sua equazione diventa, per ragioni di simmetria:

y = - ax² + c  .... (1)

Le due radici (y = 0) sono simmetriche rispetto all'asse y e si ottengono risolvendo

x² = c/a .

La gittata G è, perciò, proprio la distanza 2 √(c/a).

Analogamente a quanto fatto nella soluzione precedente, troviamo le coordinate di due punti per i quali deve passare la parabola.

Dato che la distanza tra il primo muro e il terzo è data da

2d + d = 3d    (dato del problema)

e l'ordinata è la stessa, ne consegue che l'asse delle y deve essere equidistante dai due muri, per cui possiamo scrivere le coordinate relative al punto del primo muro

x₁ = - 3d/2

y1 = h

Calcoliamo le coordinate del secondo muro, di altezza y = 15h /7

Sappiamo che la distanza tra il primo muro e il secondo è uguale a d, per cui ne segue che l'ascissa del secondo muro deve essere

x₂ = x₁ + d = - 3d/2 + d = - d/2

Sostituiamo le coordinate di questi due punti nell'equazione (1)

h= - a (- 3d/2)² + c  = a (3d/2)² + c

15h/7 = -a (-d/2)² + c = a(d/2)² + c

Dividendo entrambe le equazioni per c, otteniamo:

h/c = (a/c) (9d²/4) + 1

(15/7)(h/c) = ad²/4 + 1

e, moltiplicando la seconda per 7/15,

h/c = (a/c) (9d²/4) + 1

h/c = (7/15)(a/c)(d²/4) + 7/15

Essendo uguali i primi due membri devono essere uguali anche i secondi, per cui:

(a/c) (9/4) d² + 1 = (7/15)(a/c)(1/4)d² + 7/15

(a/c) (7/60 - 9/4) d² = 1 - 7/15

(a/c)(-128/60)d² = - 8/15

(a/c) d² = (- 8/15)(- 60/128) = 1/4

a/c = 1/(d²)4

c/a = 4d²

G = 2 √c/a = 2√(4d²) = 4d

Soluzione di Arturo

Ci siamo messi nella situazione più generica, non facendo passare la parabola per l'origine (prima soluzione) e nemmeno con l'asse y passante per il vertice (seconda soluzione), dove le intersezioni sono equidistanti, ma opposte come segno. Ne consegue che l'equazione deve essere presa senza alcuna semplificazione.

y = ax² + bx + c          .... (1)

L'origine viene posta in modo che l'asse y coincida con il primo muro.

Poiché il proiettile passa per per il punto più alto dei tre muri, la parabola passerà per i punti:

A = (0, h)

B = (d, (15/7) h)

C = (3d, h)

Sostituendo ciascun punto nella (1) si ottiene un sistema di 3 equazioni in tre incognite che permette di trovare i coefficienti a, b e c . In realtà, la prima equazione permette immediatamente di porre h = c (le equazioni diventano solo due). Alla fine si ottiene l'equazione della parabola:

          (1)

Per trovare la gittata bisogna  cercare i punti della parabola con ordinata nulla, che, ovviamente, sono due, imponendo y=0 nella suddetta equazione (e già così si vede che, potendo eliminare la h, la soluzione del problema è indipendente dall'altezza dei muri). Risolvendo la conseguente equazione di secondo grado in x, alla fine si trova:

x₁ = - (1/2) d

x₂= (7/2) d

La gittata sarà data dalla somma dei valori assoluti delle due suddette ascisse:

G = 1/2 d + 7/2 d = 4d

Io direi che i tre metodi possono considerarsi equivalenti.

Un dovuto "bravo!" anche a Michele che risolve uno dei punti fondamentali, considerando l'asse di simmetria della parabola (come fatto da Leandro):

"I punti posti ad altezza h del primo e terzo muro sono simmetrici rispetto all'asse di simmetria  della parabola che passa per essi e per il punto posto ad altezza 15/7 h.

Dai dati del quiz i punti alti del primo e terzo muro distano dall'asse di simmetria (d+2d)/2 = 3/2 d. Se il cannone fosse posto alla sommità del primo muro la gittata G sarebbe 3/2d + 3/2d = 3d.

La gittata è maggiore.

La distanza del secondo muro (quello alto 15/7 h) dall'asse di simmetria è 3/2d - d = 1/2 d"

Dopo di che risolve il tutto graficamente (bastava che imponesse il passaggio della parabola per due punti...) e trova la soluzione esatta. Un esercizio non completato analiticamente, ma che ha permesso di pensare e di trovare il nocciolo del problema.

Prima di lasciarvi, voglio ricordare che questo problema è stato dato all'Università di Dublino. E viene anche riportata la soluzione che è tutto fuorché semplice. Anzi si complica inutilmente la vita. Per pura curiosità voglio riportarla velocemente...

Soluzione "irlandese"

L'origine è preso nel primo punto in cui y = 0 (come nella nostra prima soluzione)

y = ax − bx²         .... (1)

G =nd     è la gittata, espressa come un numero moltiplicato per d.

Si ottiene la prima relazione: ponendo y =0 nella (1)

a - bx = 0

x è proprio la gittata, per cui:

a = bnd                    .... (2)

La gittata vale anche

G = nr = c + d +2d + c

da cui:

c = (n−3) (d/2)           .... (3)

c è la distanza tra l'origine e il primo muro che deve anche essere uguale alla distanza tra il terzo muro e il punto di caduta del proiettile.

La traiettoria passa per i tre punti di coordinate (c,h), (c+d, (15/7)h) e (c+ 3r, h)

Inserendoli nella equazione della parabola si ottiene:

h = ac − bc²           .... (4)

15h/7 = a(c+d) − b(c+d)²           .... (5)

h = a(c+3d) − b(c+3d)²                .... (6)

Combinando tra loro le (2), (3), (4), (5) e (6) si ottiene un sistema di 5 equazioni che risolto dà:

n = 4

Tutto giusto, ovviamente... ma perché complicarsi la vita inserendo delle incognite che tali non sono? E' un po' lo stile inglese... forse. In ogni modo... Italia-Irlanda 2-0 (almeno)!