Categorie: Articoli Fisica Fisica classica
Tags: ar70/90 beretta fisica fisica classica quantità di moto quiz
Scritto da: Arturo Lorenzo
Commenti:9
Quiz: il soldato e il laghetto di notte
Sono le ore 02:30. Un soldato si trova di notte e da solo su una piccola e leggera barca in vetroresina a remi, immobile, come il pelo dell'acqua, al centro di un laghetto di forma circolare, di raggio R=100m, dove si era recato per una esercitazione. Purtroppo, durante l'esercitazione i remi sono caduti in acqua e non sono più recuperabili. Ora deve tornare a riva nella direzione indicata dalla prua della barca. Ha soltanto il suo fucile, un Beretta AR 70/90, con un solo colpo in canna, un proiettile di massa 4 grammi. Non c'è un filo di vento e la barca non si schioda dal centro del laghetto, anche se l'attrito tra barca e acqua è assolutamente trascurabile, come pure quello con l'aria. Tutto sommato, la massa della barca con il soldato e il suo armamentario sopra ammonta complessivamente a 160 kg. Basterebbe una bava di vento , ma niente da fare, bonaccia ! E resterà bonaccia anche per le prossime ore. Come se non bastasse, il soldato, curiosamente, non sa nuotare, né l'imbarcazione è dotata di canotto di salvataggio, né di salvagente o altra attrezzatura che gli consenta di tornare a riva abbandonando la barca. Infine, il soldato non può neanche pensare di farcela cercando di usare la sue braccia come remi, perché la barca, pur essendo di piccole dimensioni, è troppo alta per consentirgli di raggiungere il pelo dell'acqua con le mani, anche se si aiutasse con il fucile.
Quesito: il soldato ha qualche possibilità di tornare a riva, utilizzando esclusivamente ciò che ha a disposizione, prima dell'alba ?
Vediamo se possiamo aiutarlo...
9 commenti
Se si ritengono trascurabili l'attrito della barca sia con l'acqua che con l'aria si può applicare il principio di conservazione della quantità di moto al sistema:
il sistema è costituito dalla barca e da tutto ciò che vi è sopra: il soldato, il fucile...
se non intervengono azioni esterne sul sistema la quantità di moto si mantiene costane ovvero se tutto è fermo (v=0 per tutti i componenti del sistema) la quantità di moto è nulla. se il soldato spara con il fucile in direzione verso il bordo della riva la barca procederà in direzione opposta.
Questo perché applicando il principio della conservazione della quantità di moto al sistema isolato dovrà risultare nulla la quantità di moto del sistema stesso:
Supposto che la velocitò del proiettile in uscita dalla Beretta sia V= 920m/s avremo:
Mbarca * vbara - mproiettile * vproiettile = 0
160* vbarca = 0,005 * 920 da cui Vbarca =9,02875 m/s
con questa velocità la barca dal centro del lago raggiunge la riva nel tempo t= 50/0,02875 =1739,1 s
circa 29 min
L’energia cinetica ½ m v^2
Oppure F = m * a, (forza uguale massa per accelerazione).
Il soldato sente la forza che spinge nel verso opposto.
Siamo sicuri che non sia un pompiere che deve imparare a nuotare di notte?
Gianfranco, scusami, non ho capito cosa intendi dire nei primi tre righi della tua risposta. Puoi esplicitare la tua soluzione ?
Prima riga: La formula dell’energia cinetica
E=1/2*M*V^2
Un proiettile di massa (M) 0,005 Kg con velocità (V) di 920 m/s
possiede una energia cinetica: E=1/2*0,005*920^2 J = 2116 J
Riga 2 : Pensavo alla formula
F = m*a
Supponiamo che la forza F di rinculo sia costante e duri 1 s
a = v/t = 920/1 = 920 m/s^2
M barca * a barca = 0,005 * 920 = 4,6
a barca = 4,6/160 = 0,02875 m/s^2
Velocità barca = a barca * t = 0,02875 m/s
Quasi 60 minuti per compiere l’intero raggio di 100 metri.
scusate correggo le ultime quattro righe della soluzione da me data al quiz:
Mbarca * Vbarca + m proiettile * vpriettile = 0
160 * Vbarca + 0,004 * 920 = 0
da cui: Vbarca = - 0,004 * 920/160 = - 0,023 m/s (la velocità barca è negativa perché opposta a quella del proietto)
con questa velocita la barca raggiunge la riva partendo dal centro del lago (di raggio 100 m) nel tempo
t = 100/0,023 = 4347,8 s circa 72 minuti
Avevo erroneamente scambiato il raggio con il diametro del lago inoltre la massa del proietto è 4 g e non 5 g
Veramente ci mette un po' di meno , infatti le due masse relativistiche devono essere moltiplicate per il rispettivo fattore di Lorentz.
Non solo, dal punto di vista del soldato in moto, il raggio del laghetto deve forzatamente essere inferiore a 100m
Leandro, il quiz è su argomenti di fisica classica. Quindi, possiamo assolutamente trascurare dilatazioni dei tempi, contrazioni delle lunghezze e variazioni della massa, considerate le velocità estremamente basse in gioco, rispetto a quelle della luce nel vuoto.
Precedentemente ho messo come massa della barca (comprensiva del soldato, il fucile, la pallottola...) il valore complessivo dato pari a 160 kg.
Non è esatto considerare questo valore dall'istante dello sparo del proiettile la cui massa è 0,004 kg.
Nel calcolo della quantità di moto del sistema dopo lo sparo (che deve essere nulla per la conservazione della quantità di moto) debbono essere considerate le due:
pbarca = (160 - 0,004)* v barca = (159,995 * v barca) kg m/s
Pproiettile = 0,004* 920 = 3,68 kg m/s
segue pbarca +Pproiettile = 0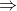
v barca = - 3,68/159,995 = 0,023 m/s
Il risultato numerico è approssimativamente uguale a quello precedente ma formalmente inesatto per quanto riguarda il calcolo delle quantità di moto con le rispettive masse in gioco