Lo scopo principale di questo esercizio era quello di ricavare, dalle più note formule della cinematica, la cosiddetta "formula senza tempo", ossia quella che lega la velocità raggiunta da un corpo, in funzione della velocità di partenza e dell'accelerazione a cui è sottoposta (sparisce il tempo).

v² = v₀² + 2a(x – x₀)

Per arrivarci mi limito alla cinematica, anche se Umberto arriva allo stesso risultato attraverso la conservazione dell'energia (e così pure Francesco, anche se non riesce a esplicitare il risultato per motivi ... tecnici)

Io parto dalla classica formula del moto uniformemente accelerato, in cui u₀ è la velocità di partenza e a l'accelerazione.

u = u₀ + at

t = (u – u₀)/a

la legge oraria ci dice anche che:

x = x₀ + u₀t + at²/2

x = x₀ + u₀(u – u₀)/a + a (u – u₀)²/2a²

x = x₀ + u₀u/a – u₀²/a + u²/2a + u₀²/2a - 2uu₀/2a

x = x₀  – u₀²/2a + u²/2a

2a(x – x₀) = u² – u₀²

u² = u₀² + 2a(x – x₀)              ..... (1)

C.V.D.

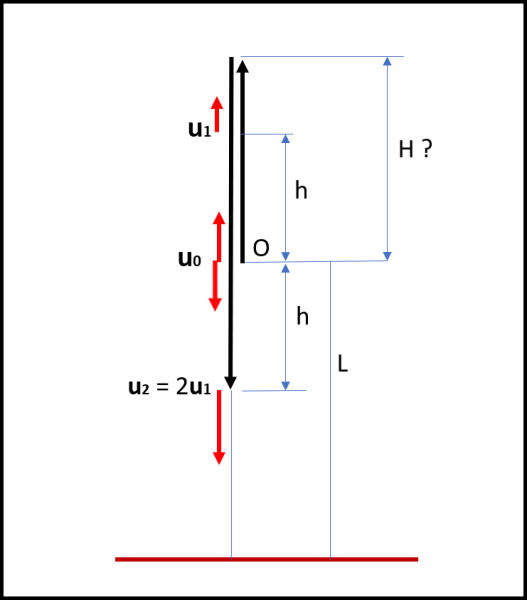
Nel nostro caso, il punto di partenza è O, con a = g e x - x₀ = h            (percorso in salita)

u₁² = u₀² - 2gh             .... (2)

Sapendo che la velocità della pietra, al nuovo passaggio dall'origine O, durante la sua discesa, deve essere uguale a u_o, con verso opposto (simmetria della legge oraria del moto uniformemente accelerato rispetto alla massima altezza raggiunta),possiamo scrivere, per il tratto in discesa sempre uguale a h:

u₂² = u_o² + 2hg           .... (3)  (il segno più sta a indicare che si viaggia nello stesso verso dell'accelerazione di gravità)

---------------------------------------------------------------------------------------------------------------------

Seguendo Umberto...

Alla stessa formula si può arrivare con la conservazione dell'energia:

La differenza di energia cinetica deve essere uguale alla differenza di energia potenziale. Prendiamo come esempio la pietra che cade verso il basso per un tragitto uguale a h, partendo da una velocità uo, Quando arriva al punto in cui raggiunge u₂, ha percorso il tratto h. 

1/2 mu₂² - 1/2 mu_o = mgL - mg(L - h) = mgh    (dove L è l'altezza di O dal suolo)

u₂² - u_o² = 2hg

In pratica, la formula (1) esprime la conservazione dell'energia!

---------------------------------------------------------------------------------------------------------------------

Sappiamo anche che

u₂ = 2u₁                  .... (4)

per cui si ottiene:

4u₁² = u₀²  + 2gh               .... (5)

Moltiplichiamo la (2) per 4

4u₁² = 4u₀² - 8gh     …. (6)

Sottraiamo la (5) dalla (6) e si ha:

3u₀² - 10gh = 0

u₀² = 10gh/3         …. (7)

la massima altezza H si ha quando u₁ della (2) si azzera, ossia quando:

0 = u₀² – 2gH          .... (8)

H = u₀²/2g

Ma, ricordando la (7):

H = 10gh/6g = 10h/6

H = 5h/3

Non aggiungo la soluzione di Arturo (che trovate nei commenti), dato che è molto simile alla mia ed è puramente cinematica.