Non tener conto delle vere lunghezze può portare a conclusioni sia matematiche che fisiche anche molto discordanti con la realtà dei fatti. La Luna lo dimostra...

Ma attorno a chi gira, veramente, la Luna?

Prendete una matita e provate a disegnare il Sole al centro di un cerchio che rappresenta l'orbita terrestre. Fatto?

Adesso indicate con un puntino la Luna nuova e disegnate a istinto la traiettoria che percorrerà nei tre o quattro giorni successivi.

Avete fatto un disegno così, o così, oppure così?

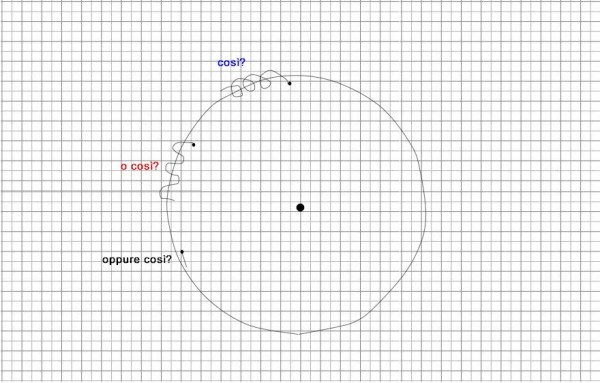
Mettete da parte il disegno e andate avanti a leggere.

Che la Luna ruoti attorno alla Terra, lo si vede ogni notte. In realtà le cose che si vedono ogni notte sono due: la Terra gira su se stessa (per cui vediamo tutto l'universo “girare” attorno a noi, Luna compresa), in più, se ad una certa ora osserviamo dove si trova la Luna, potremo notare che , rispetto alla notte precedente, risulta “arretrata”.

Questo secondo fatto lo si percepisce molto bene al momento in cui la Luna sorge, dato che apparirà all'orizzonte quasi un'ora dopo rispetto al nostro “ieri”.

Osservando la scena da sopra il polo Nord terrestre, si vedrebbe la Terra ruotare su se stessa in senso antiorario e la Luna girarle attorno in senso antiorario, guadagnando terreno, il che ha come conseguenza il ritardo di levata giorno dopo giorno.

Visto dal punto di osservazione sull'asse terrestre il percorso della Luna appare ellittico, con una differenza sensibile tra la minima e la massima distanza dalla terra. La variazione è da 356.000 a 407.000 , con una distanza media di 384.000 Km

Invece di dire che la Luna ruota intorno alla Terra, potremmo dire che ambedue ruotano attorno al baricentro del sistema che, insieme, costituiscono.

Ecco alcuni dati sui due corpi:

Caratteristica	Terra	Luna	Rapporto terra/luna
Raggio medio Km	6371	1738	3,7
Volume Km3	1,08*1012	22*109	49
Densità g/cm3	5,5	3,34	1,6
Massa Kg	5,97*1024	7,35*1022	81

Pensiamo ad un modello piuttosto rudimentale ma efficace per il nostro scopo.

La sfera Luna, con massa unitaria, si trova ad una distanza di 384.000 Km dalla sfera Terra, con massa 81 volte maggiore. Il punto di rotazione comune sarà quindi posizionato nel baricentro, a 1/81 di 384.000 Km dal centro della Terra, ossia a 4740 Km, in altri termini “dentro” il pianeta, seppellito a 1631 Km dalla superficie.

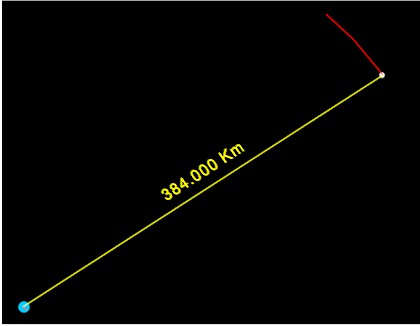
Attorno a questo punto la Luna percorre un cerchio (sappiamo che in realtà è una ellisse, ma possiamo approssimarla ad un cerchio senza compiere errori madornali) di cui nella figura vediamo un arco. Anche la Terra compie un arco, in senso opposto, ruotando attorno al medesimo punto, ma per il fatto che il baricentro “Terra-Luna” è così vicino al centro terrestre, l'arco percorso è così minuscolo, rappresentandolo in scala, che lo si può notare solo ingrandendo l'immagine.

Ma un osservatore meno coinvolto di chi si trova sul centro comune di rotazione, che tracciati potrà vedere?

Se prendiamo come punto di osservazione un punto al di sopra del Sole, sul suo asse, vedremo Terra e Luna che, pur interferendo tra loro, percorrono una ellisse attorno al Sole.

Immaginiamo, per il momento, di raffigurare un tratto di questa orbita come se fosse un segmento rettilineo, come se il Sole non esercitasse alcuna attrazione, e vediamo come appaiono i movimenti.

Nel corso di un anno terrestre ci sono 12,37 pleniluni, dato che il mese lunare è di 29,5 giorni.

Rapportando 360° a 12,37, otteniamo che, sotto un arco di 29°, si passa da un plenilunio al successivo. In questo periodo, se l'orbita terrestre fosse circolare e venisse percorsa a velocità angolare costante, la Terra avrebbe coperto una distanza di 76 milioni di Km pari a circa 200 volte la distanza Terra Luna.

Se rappresentiamo questa distanza con un segmento di lunghezza 20 cm, la distanza Terra Luna sarà di solo 1 mm.

Manteniamo queste proporzioni nella figura, ben sapendo però che il segmento di orbita che ora disegniamo come una retta, in realtà è un arco di ellisse (o di cerchio).

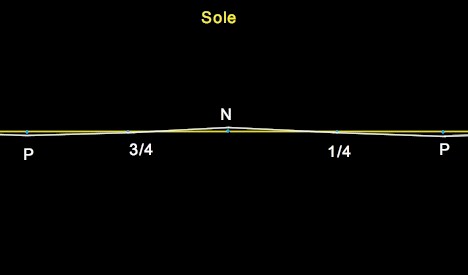
Da un Plenilunio P, al successivo, si susseguono l'ultimo quarto, il Novilunio N , il primo quarto e ancora un Plenilunio.

Il tracciato giallo rappresenta il percorso della Terra, il bianco è invece quello della Luna, che descrive una specie di sinusoide in cui il punto di massimo coincide con il Novilunio.

Da questa figura, quindi, sembrerebbe che la curvatura della traiettoria della Luna sia influenzata dalla attrazione gravitazionale della Terra, al punto di mostrare la convessità verso il Sole. In quel momento non girerebbe attorno al Sole ma attorno alla Terra.

Ma avevamo premesso che il segmento rettilineo, che rappresenta il percorso della Terra, in realtà non è affatto rettilineo, bensì è un arco di cerchio corrispondente ad un angolo di 29° perché il Sole produce con la sua presenza, con la sua attrazione gravitazionale, proprio quella curvatura.

La freccia, ossia la distanza del centro di questo arco dalla rispettiva corda è ben superiore alla distanza Terra-Luna. Con un semplice calcolo, possiamo stimare la dimensione (in milioni di Km) di questa freccia in 150 ( 1-cos (29/2°)) = 4,8 Mkm, ben maggiore della flessione, in senso opposto, della sinusoide nel momento del Novilunio.

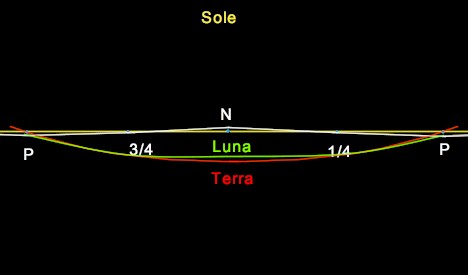
Nella figura si vede come la flessione del percorso rettilineo che lo riconduce sulla corretta traiettoria curvilinea, produca il risultato di controbilanciare abbondantemente l'effetto perturbativo della attrazione terrestre.

Questo è quanto vedrebbe approssimativamente un osservatore “fermo” sopra al Sole.

Naturalmente le approssimazioni sono molte, le orbite sono ellittiche, le velocità angolari non sono costanti (lo sono le velocità areolari), i piani orbitali sono inclinati tra di loro, gli assi di rotazione non sono perpendicolari ai piani orbitali, i moti sono molto più complessi e risentono delle imperfezioni di sfericità e non omogeneità della densità dei corpi, etc etc, ma tutto questo non inficia il semplice ragionamento geometrico descritto che, pur spiegando l'apparente rotazione della Luna attorno alla Terra, mette in chiaro che essa ruota in un'orbita molto prossima a quella terrestre, “accompagnando il pianeta madre” e intrecciando con essa il percorso.

L'orbita descritta dalla Luna (in verde) mostra costantemente la concavità verso il Sole, ed è proprio per questo che è corretto dire che il moto lunare si svolge lungo un'orbita ellittica attorno al Sole, perturbata dalla presenza della Terra. Le due orbite si intrecciano ma l'attrazione terrestre, pur riducendo la curvatura di quella lunare non è sufficiente a capovolgerla.

La Luna gira intorno al Sole e solo un pochino attorno alla Terra. Magari potete annotarlo sul vostro disegno.

Già, i vostri disegni... l'apparente differenza tra le tre figure è dovuta essenzialmente all'aver tenuto conto, o meno, delle proporzioni tra distanze e percorsi angolari. Si tratta comunque di una epicicloide, anche se nel testo l'abbiamo definita come “una specie di sinusoide”, ma la sua forma varia quanto più è “stirata” lungo il percorso, ossia la traiettoria della Terra attorno al Sole.

Quella molla arrotolata lungo la circonferenza, o l'onda che la attraversa ciclicamente, oppure il tratto di arco che l'accompagna avvicinandosi con ampia curvatura, ebbene sono tutte varianti della medesima funzione matematica. Il fatto è che riferendosi ai valori reali in gioco, come abbiamo voluto fare in questo testo, si arriva a riconoscere quale delle tre ipotesi è quella veritiera.

Se volete una spiegazione definitiva del motivo per cui l'orbita lunare è sempre curvata verso il Sole, basta ragionare sulle forze in gioco, applicando la legge di gravitazione universale di Newton.

La forza che il Sole esercita sulla Luna è: F sl = G Ms*ml / (150*10⁶ )²

La forza che la Terra esercita sulla Luna è: F tl = Gmt * ml/ 0,38*10⁶ )²

Dividiamo la forza esercitata dal Sole per quella esercitata dalla Terra. Scompaiono G e la massa della Luna ml. Il rapporto tra la massa del Sole e quella della Terra è 333.000, il rapporto inverso tra i quadrati delle distanze è (0,38/150)² = 6,4*10^-6

Quindi il risultato finale, prodotto di questi due valori, è 2,14.

Il Sole esercita un'attrazione più che doppia di quella della Terra.

In questa immagine conclusiva vediamo il passaggio dal Plenilunio P al novilunio N, con l'incrocio delle orbite all'ultimo quarto.

Dopo questo incrocio, la curvatura della linea bianca si riduce, come abbiamo visto, perché la luna viene “trattenuta” dalla Terra , che si muove sulla sua orbita, ora più esterna.

Tutto riassunto, senza bisogno di altri commenti, in questa bella animazione offerta dal Planetario di Milano:

 

La “locandina” di alcuni link alla Luna nell'archivio del Teatro.

http://www.infinitoteatrodelcosmo.it/tag/che-fai-tu-luna-in-ciel/

http://www.infinitoteatrodelcosmo.it/2017/02/11/i-racconti-di-ciccio-e-astericcio-appendice-alla-9-puntata-dalla-mela-alla-luna/

http://www.infinitoteatrodelcosmo.it/2018/04/20/leonardo-e-la-luna/

http://www.infinitoteatrodelcosmo.it/2018/04/13/la-curva-lunare/

 

E sulle cicloidi, epicicloidi relative alla Luna o ad altro, sul moto di librazione, sulla faccia nascosta o seminascosta del nostro satellite, e su come ruota,  potete vedere anche  questi altri link: 

 

http://www.infinitoteatrodelcosmo.it/2018/02/20/soluzione-dei-quiz-sulle-monete-rotolano/

http://www.infinitoteatrodelcosmo.it/2016/11/11/soluzione-del-quiz-della-terra-impazzita/

http://www.infinitoteatrodelcosmo.it/2015/12/26/quiz-la-danza-della-luna/

http://www.infinitoteatrodelcosmo.it/2015/12/28/al-quiz-rispondiamo-con-un-quiz/

http://www.infinitoteatrodelcosmo.it/2014/05/31/capire-linterno-guardando-lesterno/

https://www.astronomia.com/2012/07/30/come-ruota-la-luna/