Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Nel primo articolo abbiamo parlato di omotopie e di gruppo fondamentale. Ricordo che il gruppo fondamentale è un insieme, e precisamente l'insieme quoziente dell'insieme dei cappi su X (spazio topologico)  che  sono omotopi, ovvero riducibili uno all'altro con una trasformazione continua. In qualche modo (ossia qualitativamente) abbiamo verificato tale insieme nel caso della circonferenza e del toro. Ricordate il piano proiettivo? Lo abbiamo visto qui di recente. Che cosa sarà il gruppo fondamentale del piano proiettivo? Bè, non è proprio la cosa più semplice da calcolare. Per farlo esiste un teorema , Il teorema di Van Kampen, uno dei più importanti della topologia algebrica, ed  uno dei principali strumenti per il calcolo del gruppo fondamentale. Il teorema è in grado di calcolare il gruppo fondamentale di uno spazio topologico X partendo dal calcolo su due aperti A,B di cui esso è unione.

In questo caso si dimostra che il gruppo fondamentale del piano proiettivo è composto da due elementi; il cappio costante (un punto) ed un altro cappio.  Si dice anche che il gruppo del piano proiettivo è  isomorfo a  (classe di resti modulo 2, consta di due elementi 0,1).

Per capire bene da dove scaturisce l'enunciato della congettura, dobbiamo prima parlare di superfici e della loro classificazione.

Parliamo di superfici

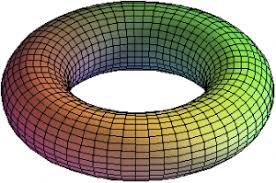
Sappiamo che nel  caso n=2, le varietà topologiche sono le superfici. Abbiamo trattato nella nostra prima serie topologica, tutte le superfici più importanti e che maggiormente ci interessano. Sfera, cilindro e toro sono  esempi di superfici orientabili;

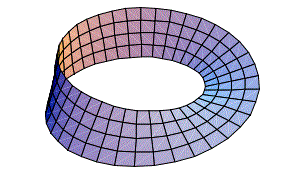
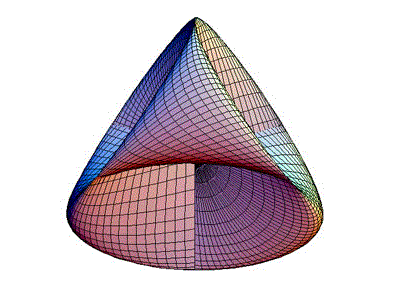
mentre il nastro di MÖBIUS , la bottiglia di Klein e il piano proiettivo sono altrettanti esempi di superfici non orientabili.

Quello che hanno dimostrato i matematici, è che qualsiasi superficie compatta e connessa si può ottenere come somma connessa  di alcune di queste superfici fondamentali. Ma cos'è la somma connessa?

La somma connessa di superfici.

Con la topologia quoziente ci siamo divertiti a costruire nuovi spazi topologici incollando i lati di un quadrato in vari  modi. Supponiamo ora di avere due superfici S1, S2 compatte e di scegliere due punti x,y su di esse.

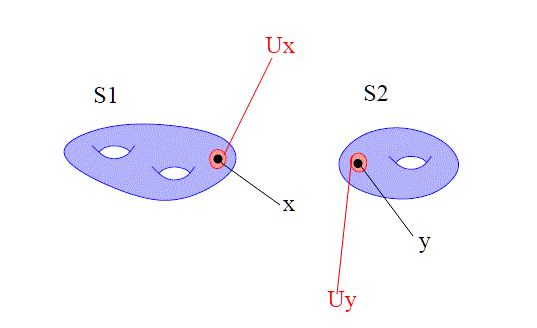
Consideriamo due intorni "tondi" di x e y, rispettivamente Ux e Uy. Con "tondi" si intende che siano omeomorfi a , ovvero al disco unitario del piano. Consideriamo i bordi di Ux e Uy, rispettivamente .  Senza entrare troppo nei particolari tecnici, incolliamo i due bordi .  Otteniamo al solito uno spazio quoziente; tale spazio, che chiamiamo S è connesso e compatto, ed è una superficie detta somma connessa di S1, S2 e indichiamo tale somma con il simbolo #:

S=S1#S2

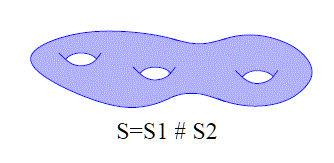
La somma connessa non dipende, a meno di omeomorfismi, dai punti scelti x,y.

La classificazione delle varietà

Un problema base  della topologia è la classificazione delle varietà topologiche.Esistono più teoremi o metodi di classificazione.
Soffermiamoci per ora alle  le varietà di dimensione 1 e 2; una varietà connessa di dimensione 1 (una linea) è  omeomorfa alla circonferenza se è  compatta o alla retta se non lo è. Per le varietà a 2 dimensioni ,una varietà a 2 dimensioni connessa e compatta è  omeomorfa alla sfera o ad una somma connessa di tori se è orientabile o ad una somma connessa di piani proiettivi se non è orientabile.  Questo appena annunciato è un teorema importante, che però non possiamo dimostrare*.

(*)In realtà tutto si può fare.. intendo fare una cernita dei risultati più importanti e fare degli approfondimenti a parte con la dimostrazione di tali teoremi.)

Il teorema scritto formalmente:

1)Teorema di classificazione delle superfici:

Ogni superficie connessa,chiusa*  e compatta è omeomorfa ad una delle superfici:

1. la sfera 
2. Una somma connessa di tori: 
3. Una somma connessa di piani proiettivi: 

(*Ricordo che una superficie chiusa è una superficie senza bordo, che è poi orientabile se non contiene alcun nastro di Mobius.)

Ma vediamo due esempi importanti:

 

La somma connessa di due piani proiettivi dà la bottiglia di klein.

Conseguenze del teorema  di classificazione delle superfici.

Tenendo fede all' enunciato originale della congettura,possiamo metterci nelle ipotesi del teorema di classificazione; avremo una superficie M compatta, chiusa ed orientabile.

Dal teorema di classificazione risulta che l'unica superficie M compatta, chiusa ed orientabile e in più semplicemente connessa è la sfera.Consideriamo infatti una superficie compatta  M semplicemente connessa.  Sappiamo che per M il gruppo fondamentale è quello banale, essendo semplicemente connessa. Si vede però intuitivamente che la somma connessa di più tori non può avere un gruppo fondamentale banale (sappiamo che il toro ha gruppo fondamentale Z x Z). M non può essere nemmeno somma connessa di piani proiettivi, in quanto tali piani non sono orientabili, mentre M si. Per cui M può essere omemomorfa solo alla sfera.

Si ha pertanto il seguente risultato, ben noto a Poincarè:

Teorema:

Una superficie chiusa,compatta semplicemente connessa *, orientabile è omeomorfa alla sfera .

(*ricordiamoci che una superficie semplicemente connessa è connessa per archi, e che una superficie connessa per archi è connessa)

E qui cominciano.. i guai. Poincarè cominciò a pensare alle varietà di dimensione n=3. Per esse non esisteva allora un teorema di classificazione, pertanto risultò naturale enunciare la congettura:

Congettura di Poincarè:
Ogni varietà tridimensionale chiusa,compatta e semplicemente connessa è omeomorfa (deformabile) alla 3–sfera.

Quindi per n=3, varrebbe lo stesso teorema che per n=2. Non ci occuperemo di altre dimensioni; oltretutto in certi casi, per n=4 la congettura è stata dimostrata in modo abbastanza diretto. Per n=3, ci sono invece voluti 100 anni.

Nel prossimo articolo cercheremo di chiarire dettagliatamente cos'è un varietà tridimensionale, anche detta tri-varietà , e quale sia la sua importanza nella conoscenza della forma dell' universo.