L'orologio a luce messo in orizzontale ci dona subito una risposta positiva... ma anche il grande amico Minkowski.

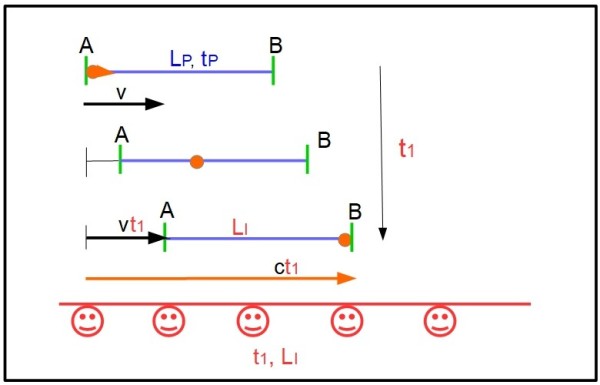
Noi sappiamo che la lunghezza misurata dall'osservatore fermo deve essere data, all'andata, da L1 = ct1  e al ritorno da L2 = ct2. t1 e t2 sono i tempi impropri che, chi è fermo, misura tra la partenza da poppa e l'arrivo della luce a prora e quello della luce che torna indietro e arriva a poppa. Nel primo caso la luce deve fare un percorso più lungo dato che l'astronave si muove con velocità v e, quindi, la prora  si allontana dal punto di partenza. Nel secondo caso, la poppa si avvicina alla luce che torna indietro. La lunghezza dell'astronave, come sarebbe vista da chi è fermo  (lunghezza impropria) sia L_I. Abbiamo allora:

L1 = c t1 = L_I + vt1           .... (1)

Questa relazione vuole dire che la lunghezza misurata all'andata è uguale alla lunghezza impropria dell'astronave più la lunghezza che la luce ha percorso per raggiungere la prua che le scappa in avanti con velocità v. Ovviamente più è grande v e più è grande il percorso aggiuntivo.

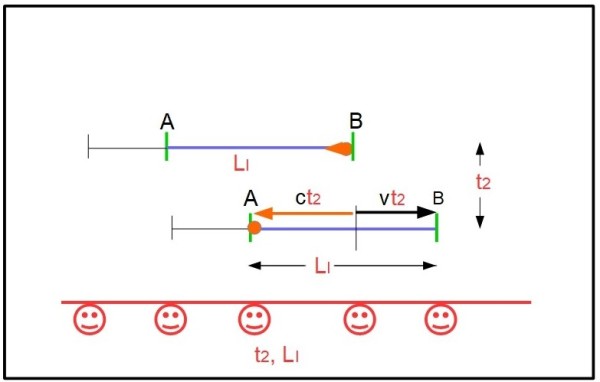
Al ritorno, invece, la luce percorre una lunghezza minore di quella impropria dell'astronave, dato che la poppa gli viene incontro. Vale perciò

L2 = ct2 = L_I - vt2            .... (2)

Dalle relazioni L1 = ct1 e L2 = ct2 si ricavano subito t1 e t2 e la (1) e la (2) formano un sistema di due equazione in due incognite: L_I e v.

L2 + vt2 = L1 - vt1

v(t2 + t1) = L1 - L2

v = (L1 - L2)/(t2 + t1)       .... (3)

Conoscendo v si ricava il fattore di Lorentz e poi, trovata L_I dalla (1) 0 (2), la lunghezza propria dell'astronave.

Proprio come spiegato nella Favola di Muo...

N.B.: In questo caso, dato che si conoscono i tempi di andata e ritorno, si poteva subito arrivare alla formuletta (3), pensando che il tragitto percorso dall'astronave tra andata e ritorno della luce non può che essere L1 - L2 (partenza e ritorno della luce a poppa) eseguito nel tempo t2 - t1. La velocità è proprio lo spazio percorso diviso il tempo.

 

 

Il diagramma di Minkowski rende immediatamente visibile la determinazione di v fatta nella nota.
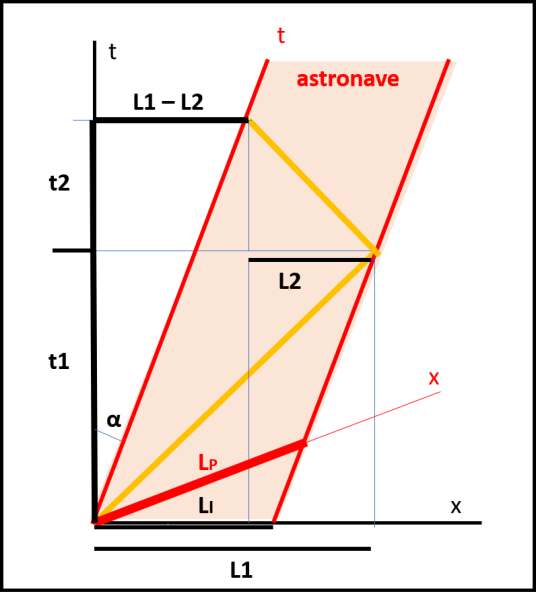Sappiamo che v è uguale a una distanza percorsa in un certo tempo. La luce fa un viaggio verso destra e poi torna indietro verso sinistra. Questi due punti indicano la direzione dell'asse temporale della poppa della nave. Lo spostamento che si è ottenuto nel tempo t1+ t2 non è altro che L1 - L2, che, oltretutto è uguale a t1 - t2, imponendo c = 1.

la velocità v si ottiene quindi attraverso la formuletta:

v = s/t = (L1 - L2)/(t1 + t2)

O -se preferite- basta ricordare che tan(α) = v (è la stessa cosa, ovviamente)

Nota  v, si ricava L_I (lunghezza impropria dell'astronave) dalla relazione:

L_I = L2 + vt2

oppure da

L_I = L1 - vt1

Conosciuto v si conosce il fattore γ:

γ = 1/√(1 - v²)                           (c = 1)

e quindi la L_P (lunghezza propria misurabile nel sistema astronave):

L_P = L_I · γ

P.S.: Come al solito, esatte le risposte di Arturo, Umberto e Paolo... ognuna con qualche variante. E bravo anche Guido...