QUIZ:UNA BIGLIA INTRAPPOLATA ***
La figura qui sotto rappresenta un biliardo ideale a quattro buche, B1,B2,B3,B4. In tale biliardo non vi sono attriti di alcun tipo, e le biglie rimbalzano da un lato all' altro seguendo le leggi della riflessione. La velocità in modulo della biglia non viene in alcun modo rallentata dagli urti con le sponde. Quindi niente frena la biglia. Le due dimensioni del biliardo sono h=49, l=78. Non serve specificare un' unità di misura, potete considerare quella che volete.
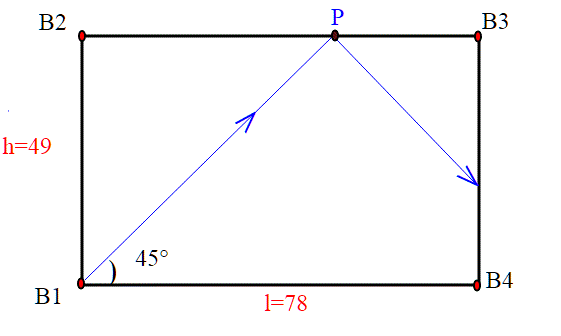
La domanda è la seguente: se lancio la biglia da B1 con un angolo di 45 gradi rispetto al segmento B1 B4 , la biglia può finire in qualche buca? Oppure è costretta a rimbalzare fra le quattro sponde all' infinito? Se la biglia finisce in una buca sapreste dire quale? E dopo quanti rimbalzi sulle sponde?
NB: questo quiz è una idealizzazione matematica. La biglia ha le dimensioni di un punto, e così pure le quattro buche. La biglia può entrare in una buca se e solo se la sua posizione istantanea nel piano del biliardo coincide con quella di una buca.






31 commenti
forse mi dà tempo per rispondere... senza dire come ho fatto (aspettiamo che si divertano tutti).
biglia nella buca in basso a destra dopo 125 rimbalzi... (risolto geometricamente, con formula ricorrente)
Bravo Umberto... bel quiz
Confermo il risultato di Vincenzo, io però ci sono arrivato... empiricamente , usando un laser abbastanza potente e 4 specchi delle dimensioni assegnate Magari più in là pubblicherò una foto.... Dimostrarlo analiticamente è ora la gatta da pelare..
Magari più in là pubblicherò una foto.... Dimostrarlo analiticamente è ora la gatta da pelare..
il solito fantastico Arturo! Ma sei riuscito anche a contare i rimbalzi?
Da quanto ho capito io la pallina entra sempre in buca se, almeno, il numeratore è maggiore del denominatore ed entrambi sono numeri interi. Non ho provato per numeratore maggiore di due volte il denominatore (ma lo farò... magari, anche se un biliardo così non esiste). Io ho usato una proprietà geometrica tipica per un angolo di 45 gradi, per adesso solo empirica, ma una ragione si deve poter trovare.
Il punto chiave, comunque, è che dopo il rimbalzo la biglia forma un triangolo isoscele al rimbalzo successivo. Da cui dovrebbe seguirne che prima di entrare in una buca deve "saturare" qualcosa...
Si, Vincenzo, conto agevolmente i rimbalzi. Anche io ne vedo 125.
Io l'ho disegnato al cad e poi gli ho fatto contare le rette "traiettoria" : ne conto 126 a cui va tolta la prima perché non nasce da rimbalzo. E quindi tornano 125 rimbalzi e buca bassa destra.
Ora sto ragionando tra MCD e perimetro: geometricamente risultano tanti segmenti paralleli ed ortogonali tra loro che convergono sui lati in punti distanziati di 2mm.
bene bene.. Vedo che il cambio di temperatura rende tutti più attivi. Ps: Abbiamo tutto il tempo che vogliamo..anche tutta una settimana.
.
Ehm... qui ancora temperatura e umidità sono alte, ma il meteo finalmente pare stia per cambiare anche qui.
Azzardo una dimostrazione, ma dico subito che non mi convince molto perché ci arrivo partendo dal dato di fatto visto empiricamente.
Quello che posso dire anche senza fare esperimenti è che a furia di rimbalzi della biglia sulle 4 sponde, il biliardo risulterà suddivisivo da tanti segmenti inclinati di 45 gradi e tra loro paralleli o ortogonali. In pratica, l'area rettangolare del biliardo risulterà suddivisa in tanti quadratini , tranne le zone adiacenti alle 4 sponde, in cui avremo dei triangoli isosceli con angoli alla base di 45 gradi. Chiamo con x la base di triangolini adiacenti alle sponde lunghe L e con y la base dei triangolini adiacenti alle sponde lunghe H. Chiamo con m il numero di rimbalzi sulla sponda B1B4 e con n il numero di rimbalzi sulla sponda B1B2. Poiché la biglia va a finire nella buca in basso a destra (e questa è una prima convinzione dovuta solo alla prova empirica...) , cioè in B4, posso subito dire che la suddivisione del biliardo in tanti quadratini e triangolini isosceli lungo le sponde è simmetrica rispetto alla mediana delle sponde lunghe (in pratica, se lanciassi la biglia da B4, anzichè da B1, essa arriverebbe in B1). Il numero di triangolini isosceli a destra delle mediana delle sponde lunghe, quindi, deve essere uguale al numero di triangolini isosceli a sinistra. Se con m ho indicato il numero di rimbalzi sulla sponda B1B4, allora il numero dei triangolini isosceli su tale sponda è m+1 (l'ultimo "tocco" della biglia sulla sponda è nella buca B4, quindi non lo considero rimbalzo). Allora deve essere (lunghezza complessiva della sponda B1B4 pari alla somma delle lunghezze della base di ciascun triangolino isoscele):
(m+1) * x = L (1)
E per la sponda corta ? Qui interviene di nuovo e "pesantemente" la constatazione dovuta alla prova empirica. In pratica si osserva che stavolta il numero di triangolini isosceli non è intero ma è pari a n+1/2 , se con n ho indicato il numero di rimbalzi sulla sponda B1B2. Dato questo fatto per appurato, allora deve essere:
(n+1/2) * y = H (2)
Ma, evidentemente, x=y (i triangolini isosceli sono tra loro congruenti), allora, combinando la (1) e la (2) alla fine ottengo:
Si tratta a questo punto di trovare una coppia di numeri interi m,n che soddisfi la (3) con i valori dati per L ed H, e una tale coppia è 38, 24. Quindi, avrò 38 rimbalzi sulla sponda B1B4, 24 rimbalzi sulla sponda B1B2 e sulla sponda B3B4 e , infine, 39 rimbalzi sulla sponda B2B3, per un totale di 125 rimbalzi.
La cosa è molto più semplice e la formula vale per tutti gli n e m.
n + m - 2 = numero di rimbalzi.
Basta dividere il lato corto in tante unità e aggiungere a un quadrato tante unità in modo da arrivare al valore del lato lungo (numeri razionali).
A questo punto basta contare quanti contatti ci sono tra la linea spezzata e il perimetro totale. Togliendo la prima e l'ultima si ha proprio m+ n - 2. O, se preferite; p/2 - 2 (p perimetro).
Allego figura
Con un angolo di 45° non sussiste la possibilità di periodicità e quindi la pallina toccando sempre TUTTI i possibili punti di contatto DEVE entrare in buca. L'importante è che li tocchi tutti!
Ovviamente, una linea spezzata così semplice può costruirsi dato che l'angolo è di 45°.
Sarebbe interessante usare un angolo di 30° (o 60°). Se ho voglia ci provo...
aspetto a parlare anche perché le idee sono buone..aspettiamo anche gli altri
si. Dopo sette rimbalzi
come mai dici 7 Gianluca ?. Non sei in linea con gli altri; hai altre idee?
Direi che la faccenda si risolve costruendo un quadrato di lato mn. Ne segue, intanto, che il percorso completo della biglia è la diagonale del quadrato (√2 mn). Ed è immediato trovare il numero di rimbalzi (escludendo il primo e l'ultimo), dato che sono proprio m-1 e n-1. Sommandoli m + n - 2.
Basta interpretare la figura che segue... lascio a voi la spiegazione (quiz nel quiz... alla Arturo ).
).
In pratica ho eliminato i rimbalzi e fatto proseguire la biglia in linea retta, dato che i rimbalzi si possono sempre contare a intervalli stabiliti e noti... (di seguito ho fatto il caso 7/5)
La figura nel prossimo commento (avevo fatto un pasticcio ... alla Enzone)
Il professore velociszimo mi ha bruciato la risposta. Basta trovare il minimo comune multiplo di 49 e 78, cioè 3822 che è il loro prodotto. 49+78-2=125.
Ok Leandro, ma resta aperto il fatto di spiegare bene il tutto.
E in che buca finisce?
Il punto essenziale secondo me è rendere rettilineo il percorso della biglia. Entra in buca quando il percorso è ovviamente una diagonale di un quadrato. Il lato deve essere m per n per definizione. Il resto viene di conseguenza...
Spero non abbiate pensato che io abbia davvero utilizzato specchi lungi 78 e 49 metri e laser di potenza tale da restare ben visibile anche su distanze di circa 5 km...
Ebbene no, ho usato il solito laboratorietto virtuale per fisica nel piano, Algodoo, che fortunatamente implementa anche un puntatore laser per esperienze di ottica.
Eccovi l'animazione del biliardo laser (verde) . In essa faccio lo zoom prima sulla buca B1 in cui ho posizionato il laser e poi sulla buca B4, in cui va a finire il raggio laser dopo aver percorso tutto quel po'-po' di cammino:
Sono poi andato a contare i rimbalzi sulle quattro sponde e infine ho cercato di dare una giustificazione teorica , riportata nel mio precedente commento.
Giusto come divagazione, allego una seconda animazione in cui si vede cosa succede se faccio cadere la sponda lunga superiore in basso verso quella inferiore. La luce, e la matematica, regalano immagini meravigliose...
Buon ferragosto a tutti.
grazie Mago Arturo.
Più precisamente, perché la pallina laser proceda in linea retta il rettagolo si deve duplicare specularmente sul lato colpito. Per ottenere un quadrato bisogna calcolare mcm ed essendo 49 e 78 coprimi, Ci sono 49 rettangoli in orizzontale e 78 in verticale.
Ora si deve notare che ad ogni ribaltamento le buche o rimangono invariate oppure si spostano lateralmente o verticalmente in ragione del doppio del lato opposto a quello colpito.
Quindi la buca colpita sarà a distanza di un numero pari di rettangoli in senso verticale e di un numero dispari in senso orizzontale.
Le buche b1 e b4 soddisfano il vincolo verticale ma solo la b4 soddisfa il vincolo orizzontale, quindi B4 !
Ovviamente, non può esistere il caso in cui n e m siano entrambi pari... altrimenti la frazione si semplificherebbe!
Le buche possibili sono quindi solo 3 come era ovvio pensare.
Per spiegare meglio la costruzione della figura del commento delle 8:48...
Notare che i rimbalzi 5 e 6 avvengono entrambi nel lato lungo...
bene bene.. sono molto contento degli ultimi commenti. Mi sa che il quiz è stato sventrato. In ogni caso lascio aperto il discorso.. potrebbero esserci nuove idee. Quindi lettori silenti provate pure a dire la vostra.
Tanto per esplicitare meglio il discorso grafico a parole:
La proiezione (sia secondo x che y) della distanza tra due rimbalzi successivi sui lati corti è uguale a m
La proiezione (sia secondo x che y) della distanza tra due rimbalzi successivi sui lati lunghi è uguale a n
quindi con 60 gradi serviranno 251 rimbalzi e con 50 gradi ce ne vorrebbero 626, mentre rimbalzerebbe all'infinito con un angolo di 89 gradi, è corretto?
ti ringrazio per la risposta ma non ho capito che calcoli o ragionamenti fai. Dovresti esplicitarli almeno in un caso.
un angolo di 45 gradi semplifica le cose (calcoli) per via dell'intuibilità data dall'elementarità del rapporto 1:2 (rispetto all'angolo di partenza = 90 gradi);
essendo la funzione racchiusa entro i limiti (78,49) ed avendo la caratteristica dell'autoriflessività (che matematicamente corrisponde al valore assoluto) ne consegue che dalla partenza all'arrivo con il suddetto rapporto essa avrà esattamente 127 impulsi (o 125 se preferite escludere i primi due) prima di restituirci un valore intero come 78 [non sto a ripetere i calcoli che avete gia fatto sopra]. Anche il coseno della funzione avra sempre valore unitario, semplificando i calcoli per un approccio, per puro esempio, di calcolo delle fasi dell'ipotetica "onda" (anziche pallina) per ottenere il numero di rimbalzi affinche restituisca un valore intero sulle ascisse e pari ad almeno uno dei multipli di 78
gli stessi calcoli si possono in questo caso ottenere imponendo un sistema condizionato e calcolando il fattoriale dei rimbalzi
diverso diviene il discorso per angoli differenti, dove si evince immediatamente non solo la dipendenza dei rimbalzi della pallina dai limiti della struttura, ma anche dall'angolo della sua direzione;
in particolare, è semplice calcolare che, per qualsiasi limite imposto, il numero dei rimbalzi puo sapersi a priori poiche dipendente unicamente dall'angolo e dal suo coseno. Alias, importa conoscere solamente l'angolo e il relativo coseno e "confrontarlo" con la struttura del limite imposto.
ciao a tutti,
anche io ho fatto un ragionamento analogo a Vincenzo Zappalà, ma direi che più in generale dati h e l interi, ponendo n=mcm(h,l), il numero dei rimbalzi in verticale sono Rv=n/h-1, mentre quelli in orizzontale Rh=n/l-1.
Il che si riduce alla formula di Vincenzo nel caso di h e l senza divisori comuni.
Saluti e complimenti per il sito e il problema!
Andrea
grazie mille Andrea!