La soluzione che propongo io è sicuramente molto lunga, ma ha lo scopo di richiamare molti concetti importanti del moto parabolico.

Iniziamo a ricavare l’equazione della traiettoria del proiettile in funzione di α e di u_0. Un esercizio, questo, estremamente didattico che, oltretutto, serve per dimostrare che la traiettoria è proprio una parabola.

Consideriamo la Fig. 1, dove abbiamo posto l’origine degli assi nel punto di partenza del proiettile, ossia per t = 0, anche x = y = 0.

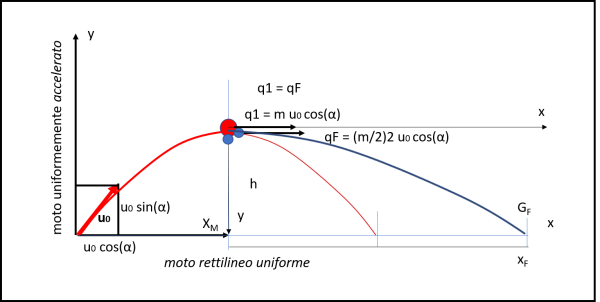
Ricordiamoci le due leggi orarie del proiettile: una è quella che corrisponde a un moto rettilineo uniforme lungo l’asse x e l’altra che corrisponde a un moto uniformemente accelerato lungo l’asse y.

x = u_0x t                            …. (1)

y = u_0y t – ½ gt²              …. (2)

Facciamo subito comparire anche l’angolo α:

u_0x = u₀ cos α

u_0y = u₀ sen α

Ricaviamo t dalla (1) e lo sostituiamo nella (2)

t = x/u_0x = x/u₀ cos α

y = x tan α - ½ g x²/(u₀² cos² α)              …. (3)

questa è un’equazione del tipo:

y = Ax² + Bx        (con A e B costanti)

ossia proprio una parabola passante per l’origine degli assi ( y = 0 per x = 0).

E’ immediato calcolare la gittata del proiettile che non è altro che il secondo valore di x che annulla la y nella (3):

0 = x (u₀ tan α - ½ g x/(u₀² cos² α))

Il primo è ovviamente x = 0

Il secondo si ottiene azzerando la parentesi che moltiplica x

tan α - ½ g x/(u₀² cos² α) = 0

½ g x/(u₀² cos² α) = tan α

x = 2 (tan α/g )(u₀² cos² α) = (2u₀²/g) (sen α cos²α/cos α) = (u₀²/g) (2 sen α cosα)    …. (4)

A questo punto, ricordiamo una famosa formula trigonometrica (addizione degli archi):

sen (α + β) = (sen α cos β) + (cos α sen β)

e poniamo α = β. Si ottiene:

sen (2α) = 2 sen α cos α

per cui la (4) diventa:

x = G1 = u₀² sen (2α)/g         …. (5)

Per quanto detto precedentemente questa è la formula che ci regala la gittata G1 in funzione di u₀ e α.

Possiamo anche dire, per la ovvia simmetria della parabola rispetto al suo vertice, che l’ascissa del punto più alto della traiettoria cade esattamente a metà della gittata. Ossia:

x_M = u₀² sen (2α)/2g                      …. (5)

Questo è proprio il punto in cui il proiettile esplode e si divide in due frammenti. Tuttavia,  è anche il punto in cui la velocità  del proiettile è solamente orizzontale, in quanto la componente lungo la y è nulla (punto di massima altezza). Quale è la quantità di moto del proiettile al momento dell’esplosione?

q1 = mu_0x = m u_o cos α        (la velocità lungo x è una costante!)

subito dopo l’esplosione (fenomeno interno al sistema!) la quantità di moto deve conservarsi e la somma delle quantità di moto dei due frammenti deve essere uguale alla quantità di moto  prima dell’esplosione. Calcoliamolo sia lungo x che lungo y.

Possiamo scrivere, per la componente lungo x:

mu_0x = mu₀ cos α = ½ mv_x

Per quella lungo y, invece si ha:

0 = ½ m v_y

Ossia v_y = 0

Si ha perciò:

v_x= 2u₀ cos α                  …. (6)

A questo punto abbiamo ottenuto la prima metà della gittata (5), quando ancora il proiettile era intero, ma, adesso, dobbiamo trovare la gittata per un proiettile sparato a una certa altezza con una velocità pari a 2u₀ cos α.

Siamo di fronte a un nuovo moto parabolico in cui il proiettile è sparato orizzontalmente a partire da una certa altezza h rispetto al suolo. A noi interessa determinare la gittata di questo secondo proiettile.

Calcoliamo, innanzitutto l’altezza h, che è anche la massima altezza del primo moto parabolico e, quindi, l’ordinata y corrispondente a x pari a metà della gittata, ossia al valore dato dalla (5) Prendiamo la (3) e sostituiamo a x il valore di x_M della (5). Questa y massima è la nostra h.

h = x_M tan α – ½ g x_M²/u₀² cos²α

h = u₀² sen (2α) tan α /2g – ½ g u₀⁴ sen² (2α) / (4g² u₀²cos²a)

h = 2 u₀² sen α cos α sen α /2 g cos α – ½ g 4 u₀⁴ sen²α cos² α /4 g²(u₀²cos² α)

h = u₀²sen² α / g – u₀² sen² α /2g

h  = u₀² sen² α/2g              …. (7)

Spostiamo l’origine degli assi nel punto di coordinate (x_M,h), il punto di massima altezza della prima parabola, e scriviamo l’equazione della traiettoria del moto parabolico (3) cambiando verso all’asse y. Ricordiamo, però, che l’angolo tra velocità e asse orizzontale è ora uguale a zero.

Otteniamo, perciò:

y = x tan(0) + ½ g x²/v_x² cos²(0) = ½ g x²/v_x²

A noi interessa trovare la x per la quale y = h. Essa sarà proprio quella del punto di caduta del frammento ossia la sua gittata.

x_F² = 2 h v_x²/g

ma noi conosciamo i valori di h (7) e di v_x (6) in funzione di u₀ e α

x_F² = 8u₀² sen² α u₀² cos² α /2g²

x_F² = 2u₀⁴ sin² (2α)/2g²

x_F = u₀² sen (2α)/g             …. (8)

A questa gittata va aggiunta quella relativa alla prima metà della traiettoria parabolica iniziale (5), ossia:

x_M = u₀² sen (2α)/2g

Sommando le due espressioni, otteniamo:

G_F = (3/2g) u₀² sen (2α)