Aguzza la mente... (con la catenaria)
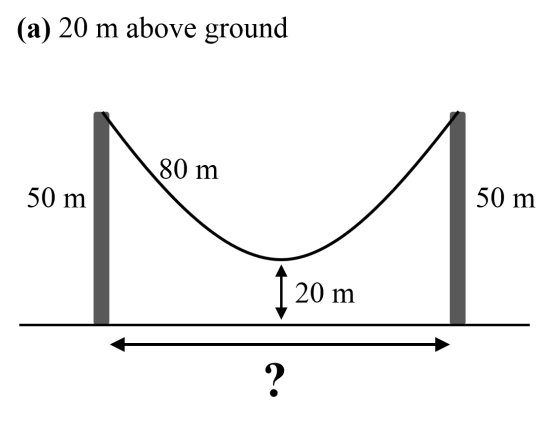
In rete si trova l'immagine allegata o altre simili a proposito di problem solving. Ma noi vogliamo scoprire qui se in tale immagine c'è qualcosa di strano. Lo scopriremo cercando di ricavare la distanza tra i i due pali. La fune è una catenaria. A voi le risposte...






25 commenti
Solo per essere sicuro: con 80m indichi la lunghezza della fune?
Si, Francesco, la figura (non mia) indica con 80m la lunghezza della fune.
Sicuramente minore di 52.91 ...
smuoviamo un po' le acque? Solo un piccolo aiuto (sibillino): la forma di una parabola simmetrica all'asse y da cosa dipende? Beh.... per la catenaria abbiamo qualcosa di simile...
o sbaglio Arturo?
Leandro, credo tu abbia considerato il triangolo rettangolo avente per ipotenusa la semi-lunghezza della fune (cioè 40m) e per cateto minore la differenza di quota tra i punti di ancoraggio e il vertice in basso della fune (cioè 30m). Ti sei ricavato così l'altro cateto con il teorema di Pitagora e hai moltiplicato per 2 per la simmetria della configurazione. La domanda però richiede un valore finito, non un intervallo di valori. Comunque ti direi che hai ragione se però non restasse qualcosa di strano nella figura... Ma la stranezza può emergere solo partendo dal fatto che la fune è una catenaria e ragionandoci su. Poiché qui sul Circolo sinora non si era ancora parlato di catenarie (e il quiz è proprio un'occasione per annunciare un prossimo articolo su questa curva) , aspetto ancora un po' e poi do un aiutino.
Non sbagli Prof.
Allego un grafico in cui si vede la catenaria (curva verde) e la parabola (curva nera) passanti per gli stessi 3 punti del quiz.
Aiutino/one (di corsa, la famigliola reclama il mare... )
)
L'equazione della catenaria, nel sistema di riferimento con asse y di simmetria della curva e origine a distanza "a" dal vertice in basso della curva, è:
L'equazione che esprime la lunghezza di un arco di catenaria dal vertice in basso al generico punto P di ascissa x in funzione di tale ascissa, sempre nel suddetto sistema di riferimento, è:
[le suddette equazioni per ora prendetele per buone, le ricaveremo passo passo nel successivo articolo sulla catenaria]
tra seno iperbolico e coseno iperbolico sussiste la relazione
Sì , svolgendo i calcoli la distanza dovrebbe essere maggiore di 120m che non si concilia con la geometria data.
tanto per riassumere quanto dice Leandro: per definire una catenaria, come per definire una parabola del tipo y = ax2, basta un solo parametro! E quindi gli altri devono essere quelli che sono e non indipendenti tra loro.
Chissà se il tuffo di Arturo seguirà una parabola o una catenaria ????? Fallo con un angolo minore di 45° così sarà ben difficile accorgersi della differenza (lo dice anche Galileo...).
Fallo con un angolo minore di 45° così sarà ben difficile accorgersi della differenza (lo dice anche Galileo...).
Provo a dare una soluzione (non essendo un matematico probabilmente scriverò "cose" non corrette):
La funzione cosh (x/a) è :
f(x) = 1/2(ex/a + ex/a)
La funzione è riferita ad un sistema di assi x0y ove il vertice della catenaria è sull'asse y e l'ordinata di detto vertice vale (a),
La curva è simmetrica rispetto all'asse y.
Nel punto di attacco della fune a dx l'ordinata vale 50 m quindi sostituendo i dati numerici ho:
cosh (x/20) = 1/2(ex/20 + e-x/20)
50/20 = 1/2(ex/20 + e-x/20)
Pongo t= ex/20
Abbiamo
2.5 = 1/2 (t + 1/t)
5 = 1/t ( t2 + 1)
5t = t2 + 1
t2 - 5t +1 = 0
Δ = 25 - 4 = 21
Rad. Δ= 4.58 (circa)
t =1/2( 5 + 4.58 ) = 4.79
t =1/2( 5 - 4.58) = 0.21
Dalla incognita ausiliaria t segue
4.79 = ex/20
0.21 = ex/20
Per definizione di logaritmo abbiamo
x/20 = ln 4.79
x = 20 ( 1.566) = 31.33...
Dalla seconda
x/20 = ln(0.21)
x = 20 ( - 1.56) = - 31.21...
Risulta accettabile solo la soluzione positiva ovvero la distanza del palo a dx dall'origine
x = 31.33
La distanza tra i pali è il doppio di x
D = 62.66 m
Correggetemi se ho scritto degli strafalcioni
Michele, il ragionamento e i calcoli mi sembrano corretti. Il problema è che se con "a" intendiamo la quota del vertice indicata nella figura, sostituendo il valore di x trovato con il procedimento che hai esposto nell'equazione che mi restituisce la lunghezza dell'arco di catenaria, otteniamo un valore di 91,65 m circa, in discordanza con la figura. L'inghippo è nel significato che diamo al coefficiente "a"...
Nella formula manca una "a" a numeratore. Infatti se x=0 allora f(x)= a =20.
grazie per la correzione Leandro, in effetti avevo dimenticato di mettere il coefficiente a nella formula del cosh
rifacendo i calcoli ho:
f(x)= a/2(ex/a + e-x/a)
sostituendo i valori numerici
50 = 20/2 (ex/20 + e-x/20)
5 = (ex/20 + e-x/20) posta l'incognita ausiliaria t = ex/20
5 = t + 1/t
5 = 1/t (t2 + 1)
05t = t2 + 1
t2 - 5t + 1 = 0
Δ = 25 -4 = 21 radice di Δ = 4.582...
t1 = 1/2 ( 5 + 4.582) = 4.791
t2 = 1/2 ( 5 - 4.582) = 0,209
sostituendo i valori all'incognita ausiliaria t
4,791 = ex/20
x/20 = ln (4,791)
x = 20 * 1.567 = 31,34
x = 20 ln ( 0.209) = 20* (-1.565) = -31,3
Avevo ommesso il valore di a ma il risultato è lo stesso di prima salvo approssimazioni.
Ma Arturo pone l'attenzione sul significato del parametro a
non riesco a dare ora una risposta; nel caso della parabola (y = ax2) se deriviamo la funzione otteniamo
dy /dx = 2ax
che geometricamente rappresenta il coefficiente angolare alla curva nel punto x: maggiore è a più elevata è la pendenza della curva nel punto x e quindi sostanzialmente cambia la forma della parabola
che significato bisogna attribuire al coefficiente a nella funzione che descrive la catenaria?
A mio parere non c'è nulla di strano: se attacco gli estremi di una catena di 80m a 2 pali alti 50m,e li metto vicini (x=0),la catena si dispone verticalmente e scende fino a 10 m dal suolo. Poi allontano i due pali fino ad avere la catena orizzontale (catena tutta a quota 50m). Quindi tutte le configurazioni tra x=0 (cioè a=10) e x=40 (a=50) sono permesse.
Applico la seconda formula (quella del seno iperbolico) : 40=20*sinh(x/20) e trovo la x, moltiplico per 2 e trovo la distanza.
Se non sbaglio il risultato è x=28.87 da cui la distanza tra i pali=57,... m
I valori li ho ricavati da una calcolatrice scientifica con l'arco seno
Volevo dire arco seno iperbolico
Francesco, anche tu stai ponendo "a"=20, cioè uguale alla quota del vertice della catenaria rispetto al suolo. Quindi, l'equazione della catenaria, nel sistema di assi cartesiani con origine a distanza "a" , in basso, dal vertice sarà:
y=20 cosh (x/20)
Dall'equazione che dà la lunghezza dell'arco di catenaria ricavi il valore di 57m per la distanza tra i punti di ancoraggio. OK, ma se, invece, prendiamo l'equazione suddetta della catenaria e la mettiamo a sistema con quella della retta y=50 (passante per i due punti di ancoraggio) , cioè se cerchiamo i punti di intersezione tra tale retta e la catenaria, troviamo:
x=+- 31,34m
quindi una distanza tra gli ancoraggi pari a 62,68m
Quale sarà il valore giusto
Dato per vero che la catena appesa in quel modo i 20m li raggiunge e dati per veri i risultati ottenuti, allora la catena non segue quella specifica catenaria. La funzione è un'altra
Ricapitolando, con riferimento alla figura, la fune è una catenaria, i punti di ancoraggio sono a 50m dal suolo, il punto più basso della fune è a 20m di altezza dal suolo, la fune è lunga 80m.
Nessuno ancora ha dato il risultato corretto per la distanza tra i pali.
Cosa è che non va ?....
Forse sbaglio ma se la freccia è 20m, la lunghezza della catena risulta oltre 120m ....
Urka mi correggo: la distanza è superiore a 190m ma come fa una catena lunga 80m a starci?
AIUTONE:
ragazzi non fatevi prendere per il naso... I 20 metri potevano anche essere 200, ma niente cambiava...
Ah, questo Artù è terribile. Era riuscito a confondere anche me (cosa facile, in realtà....).
ehm... veramente la prima volta ci sono rimasto di sasso pure io

L'ho scritto, tutto dipende da cosa intendiamo per "a"...
Mettiamola così: è meglio che il circolo non costruisca ponti con le catenarie...

Pubblicata la soluzione QUI
Grazie a tutti i partecipanti e i lettori.
Ho una domanda. Se io ho la funzione di una fune molto tesa y(x) =(qx/2H)*(l-x) dove H=tiro e q carico se io traccio il grafico questa è una parabola. Se invece ho l'equazione di una catenaria cioè una fune poco tesa y(x)=-H*(((1/(q))*cosh(q*l/(2*H)))-((1/(q))*cosh((q*(l-(2*x)))/(2*H)))) tracciando il grafico ha la forma di un coseno iperbolico. Perchè se io via via aumento il tiro nell'equazione delle funi poco tese il grafico tende a una parabola?