Intanto , grazie a tutti coloro che hanno partecipato al quiz sulla catenaria. E' sempre un piacere vedere la gente partecipare e arrovellarsi il cervello con questi argomenti anche in pieno periodo di ferragosto 

Ho proposto questo quiz perché anche io,  pensando ad un successivo articolo sulla catenaria, sono incappato nell'immagine che ho poi sottoposto alla vostra attenzione, e ho pensato che il parametro "a" che caratterizza l'equazione di una catenaria fosse uguale a 20, probabilmente spinto in questo dalla visione della scritta in testa alla figura "(a) 20m above ground".

In realtà così non è.

Ma cominciamo dall'inizio, ricordando qui l'equazione di una catenaria. E' importante precisare il sistema di riferimento cartesiano rispetto al quale indichiamo l'equazione. E', infatti, naturale che l'equazione di una curva in un dato sistema di riferimento cambi se cambia quest'ultimo. Per esempio, la retta di equazione y=10 nel sistema di riferimento con l'asse x distante 10 dalla retta , cambia in y=0 se prendo come sistema di riferimento  quello con l'asse x coincidente con la retta.

Si era detto nei commenti al quiz che l'equazione di una catenaria riferita al sistema di assi cartesiani con origine distante "a" dal vertice in basso della curva e asse y coincidente con quello di simmetria della curva è:

         (1)

avendo indicato con cosh(x/a) il coseno iperbolico di x/a, cioè

La seguente figura illustra la catenaria nel sistema di riferimento suddetto:

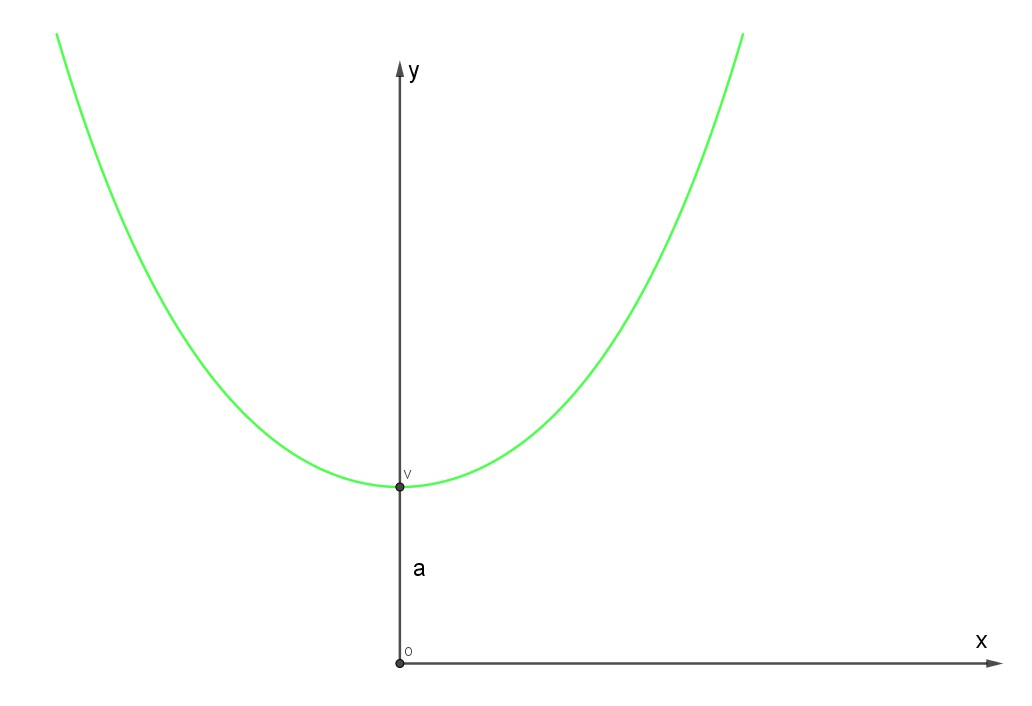
Ora, operiamo una traslazione verticale del sistema di riferimento della quantità "a". Ovviamente, nel nuovo sistema di riferimento così ottenuto, l'origine O coinciderà con il vertice V della catenaria. La sua equazione, quindi, cambierà in:

          (2)

Per convincercene basta considerare che il vertice V, che nel precedente sistema di riferimento aveva coordinate (0,a), nel nuovo sistema di riferimento ha coordinate (0,0), quindi la sua nuova ordinata è pari a quella di prima meno "a". E ciò, naturalmente, vale per tutti i punti della catenaria.

La seguente figura illustra la catenaria nel nuovo sistema di riferimento adottato. In essa ho voluto rimarcare il segmento "a", che ora sta sotto l'origine.

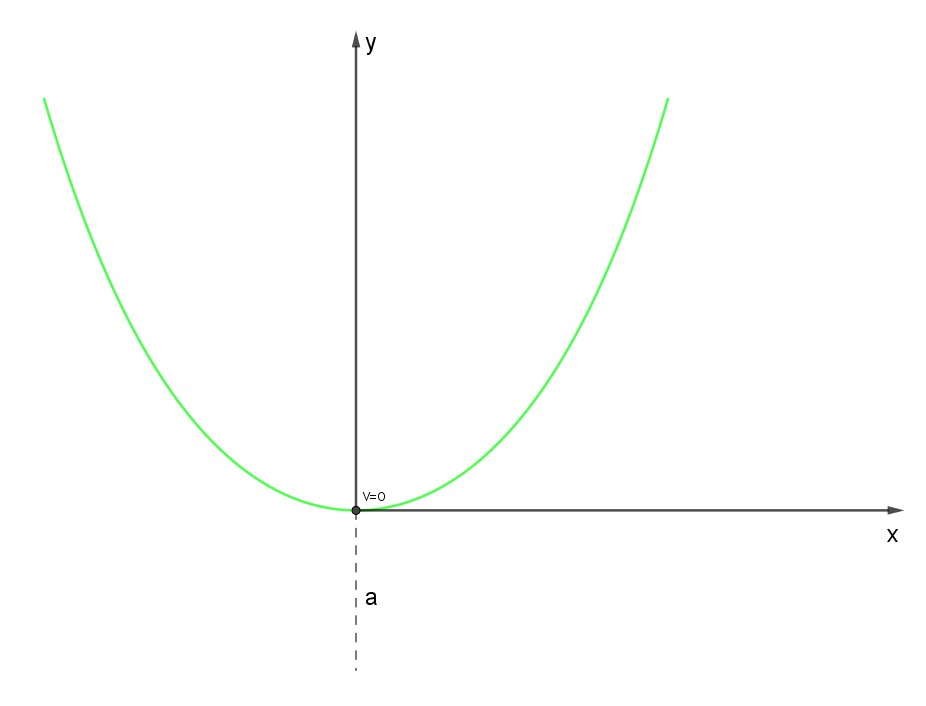
In tale sistema di riferimento, la differenza di quota tra i punti più alti della curva e il vertice, con riferimento ai dati del quiz, è chiaramente pari a 30 (50-20), ma sarebbe 30 anche in qualsiasi altro sistema di riferimento traslato rispetto a questo. Possiamo allora dire che l'ordinata dei due punti più alti della catenaria , in questo sistema di riferimento, è 30. Ci siamo ? OK, teniamo a mente questo particolare e procediamo.

Ora ragioniamo sulla catenaria nel sistema di riferimento  adottato e calcoliamoci "a" come se fosse la nostra incognita. L'equazione della catenaria è, per quanto detto, la (2). Nei commenti, inoltre, era stata pubblicata l'equazione che restituisce la lunghezza s di un arco di catenaria dal suo vertice V al generico punto P di ascissa x:

           (3)

avendo indicato con sinh(x/a) il seno iperbolico di x/a , cioè:

Tale equazione, contrariamente a quella della catenaria, è "invariante" rispetto alla traslazione degli assi. E' intuibile, infatti, che la lunghezza di un arco di curva non può cambiare se cambia il sistema di riferimento. Se l'arco è lungo 40m nel primo sistema di riferimento, resterà di 40m anche in ogni altro sistema di riferimento.

Applichiamo ora la (2) e la (3) al caso in esame. In particolare, applichiamo la (2) nel punto più alto a destra della catenaria, avente coordinate (x,30) nel sistema di riferimento adottato:

cioè, smanettando solo un pò:

                              (4)

Applichiamo ora la (3), sempre considerando il punto più alto (x,30) e sapendo, dai dati del quiz, che la lunghezza dell'arco è 40m (metà dell'intera fune):

cioè:

                                      (5)

Ora utilizziamo la relazione fondamentale della trigonometria iperbolica, anch'essa richiamata nei commenti al quiz:

               (6)

Sostiuendo le espressioni trovate in (4) e (5) risulta:

Sviluppando i quadrati, ordinando e semplificando otteniamo:

                   (=11,67m circa)

Ecco , dunque, la sorpresa: il valore del parametro "a" non è 20, come si è portati a pensare con la figura pubblicata nel quiz, ma 11,67m. A questo punto, noto il parametro "a" che caratterizza la catenaria, sappiamo tutto. In particolare, sostituiamo il valore di "a" ora trovato in una delle (4) e (5) e otteniamo l'ascissa x dei punti più alti della catenaria. Dalla (5):

da cui (utilizzando una calcolatrice scientifica, basta solo quella di Windows) :

x=22,7 m

Volendo , infine, rappresentare la catenaria del quiz con i sostegni, il vertice a 20m dal suolo etc, basterà traslare verticalmente verso l'alto della quantità hv la (2), avendo indicato con hv la quota del vertice della catenaria rispetto al suolo. Quindi:

          (7)

La seguente figura è praticamente il grafico della (7) , in essa ho inserito anche i piloni. Anche in questa figura ho lasciato in evidenza il segmento di lunghezza "a", per far vedere che è diverso da quello che pensavamo. Dalla (7) , ponendo x=0, avremo cosh(0)=1 (è come nel caso del coseno classico) , per cui y(0)=hv. Per x=22,7m , invece, attraverso la (7) otterremo y(x)=50m, mentre dalla (3) otterremo s(x)=40m (metà lunghezza della fune). Tutto torna.

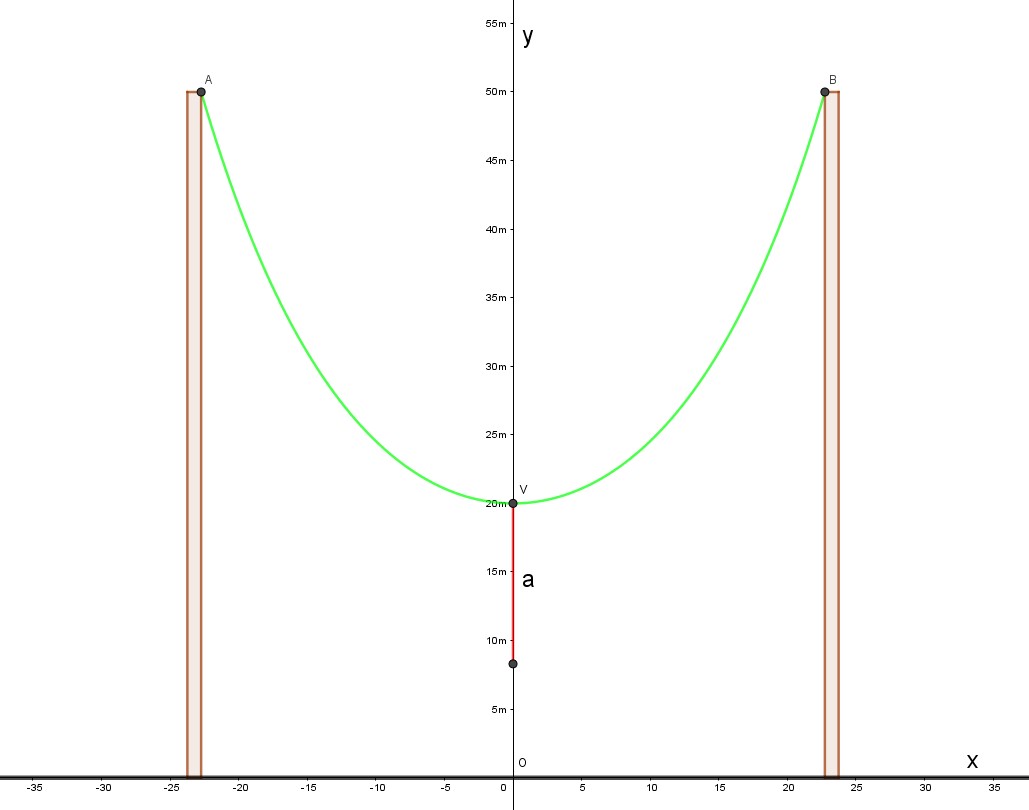
Bene, nell'annunciato articolo sulla catenaria, ricaveremo passo passo la sua equazione, partendo da considerazioni fisiche. Questa curva, infatti, è modellata dalla gravità.