22/08/19

Soluzione (parziale) del quiz sul cuneo e il cubo ****

Categorie: Fisica classica Tags: accelerazione cubo cuneo gravità quantità di moto quiz soluzione Scritto da: Vincenzo Zappalà Commenti:25

Come già detto, in fisica esistono molto spesso procedimenti diversi per risolvere un certo problema. La soluzione che riporto io potrebbe anche non essere la più rapida. La difficoltà dell’esercizio sta nella stretta relazione esistente tra il moto del cubo e quello del cuneo (e viceversa). Una sola forza si scompone e si ricompone intrecciando le accelerazioni finali dei due corpi in movimento.

Teniamo, infatti, conto che esiste un’unica forza agente sul sistema, per cui la somma delle accelerazioni deve essere uguale a quella impartita al sistema da questa sola forza.

Iniziamo dicendo che, all’inizio, tutto è fermo. Ciò vuole anche dire che la quantità di moto del sistema cuneo + cubo deve essere uguale a ZERO. Il cubo, però, comincia a scivolare e lo fa attraverso una forza esterna al sistema, ossia la forza di gravità. Tuttavia, la forza di gravità che agisce sul cubo è diretta in senso verticale. Questo vuol dire che la sua componente lungo l’asse x è nulla. Di conseguenza, la quantità di moto lungo l’asse x deve conservarsi.

Quanto vale la quantità di moto lungo quest’asse durante la discesa del cubo? Beh… vi è una parte dovuta allo spostamento del cubo verso destra che deve essere controbilanciata da quella del cuneo (la cui massa è però M + m, dato che si porta dietro anche il cubo) verso sinistra, in modo da dare come risultato ZERO. Anche se non compare, questo risultato è strettamente legato alla forza di gravità che agisce sul cubo.

In linguaggio matematico, ricordando che la velocità è la derivata dello spostamento, si ha:

(M + m) dx/dt = m ds/dt cos(α) …. (1)

ds/dt cos(α) non è altro che la componente della velocità del cubo (di massa m) lungo l’asse x, per effetto del suo scivolamento. Questo spostamento verso destra deve essere uguale a quello verso sinistra dello spostamento del cuneo e del cubo (di massa M + m), per conservare la componente della quantità di moto lungo l’asse x.

In questa espressione figurano le velocità lungo s e lungo x, ma noi siamo interessati alle accelerazioni. Nessun problema, basta derivare l’espressione rispetto al tempo, ricordando che M, m, e α sono costanti. Ne segue che la (1) diventa:

(M + m) d²x/dt²- m d²s/dt² cos(α) = 0

Possiamo tranquillamente concludere che d²x/dt² è proprio l’accelerazione del cuneo triangolare a_T, mentre ds²/dt² e quella del cubo a_C. D’altra parte, è solo il cubo che può muoversi lungo s, mentre è solo il cuneo (con il cubo sopra) che può muoversi lungo x. Notiamo, anche, che la derivata seconda non può essere zero dato che il moto non è rettilineo uniforme, ma sicuramente accelerato (il cubo varia la sua velocità di discesa e quindi anche la sua componente lungo x).

(M + m) a_T - m a_C cos(α) = 0 …. (2)

Comunque sia, non abbiamo risolto un bel niente, dato che entrambe le accelerazioni sono incognite. Abbiamo bisogno di trovare un’altra espressione che le leghi tra loro.

Abbiamo già sfruttato tutto ciò che conosciamo sul sistema cuneo + cubo? In realtà no, dato che abbiamo finora “apparentemente” trascurato la causa prima di tutto il suo movimento. Questa causa è proprio la forza di gravità che agisce sul cubo e di conseguenza anche sul cuneo. Tutto ciò che abbiamo scritto avviene di conseguenza. Le due accelerazioni scritte precedentemente devono, perciò, dipendere da una sola, quella di gravità, agente SOLO sul cubo.

Utilizziamo, allora, le due accelerazioni che compaiono nella (2), applicate al cubo, lungo una direzione in cui la forza di gravità non è nulla. Questa direzione è proprio l’asse s. Le due accelerazioni, moltiplicate per la massa m del cubo, danno luogo a due forze, la cui somma deve essere uguale all’unica forza esistente, applicata al cubo, proiettata nella direzione di s. In fondo, la volta precedente abbiamo fatto la stessa cosa, attraverso la conservazione della quantità di moto lungo l’unica direzione in cui essa si conservava, ossia l’asse x. In quella direzione la forza di gravità compare, ma la sua componente ha valore nullo.

La componente della forza di gravità agente sul cubo nella direzione dell’asse s è data da:

F = m g sin(α)

F₁ = m a_C è contenuta nella direzione s per definizione (la sua accelerazione è d²s/dt²). Lei agisce solo nella direzione s, infatti, nella (2), avevamo utilizzato la sua proiezione lungo x. Dobbiamo invece calcolare la componente dell’accelerazione subita dal cubo mentre viene trascinato dal cuneo verso sinistra. Essa non è altro che F₂ = - m a_Tcos(α). Possiamo quindi scrivere la seconda relazione che lega le accelerazioni del sistema:

F₁ – F₂ = m a_C - m a_T cos(α) = m g sin(α)

Ossia:

a_C - a_T cos(α) = g sin(α) …. (3)

La (2) e la (3) formano il sistema di cui avevamo bisogno: due equazioni in due incognite, a_Te a_C

(M + m) a_T - m a_C cos(α) = 0

a_C- a_T cos(α) = g sin(α) …. (4)

La Fig. 1 riassume il diagramma delle forze che derivano, solo e soltanto, dalla forza di gravità agente su m.

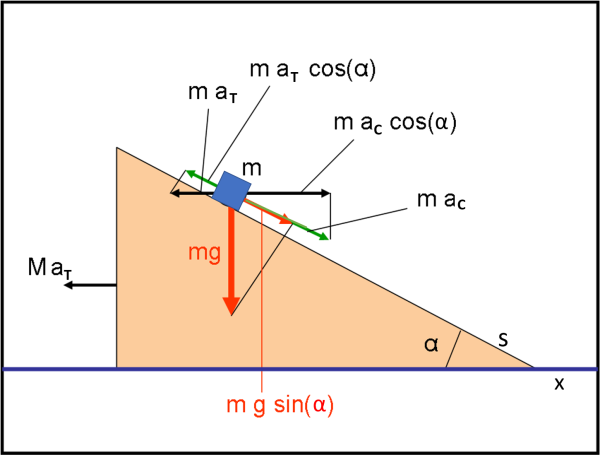
Non ci resta che risolvere il sistema…

Come al solito, conviene eseguire qualche “trucchetto”. Possiamo moltiplicare la seconda equazione della (4) per m cos(α). Otteniamo:

(M + m) a_T - m a_C cos(α) = 0

a_Cm cos(α) - m a_T cos(α) cos(α) = m g sin(α) cos(α)

sommandole, si elimina il termine in a_C e otteniamo un’equazione in cui compare solo a_T :

(M + m) a_T - m a_Tcos(α) cos(α) = m g sin(α) cos(α)

a_T(M + m - m cos²(α)) = m g sin(α) cos(α)

ricordando che

sin²(α) + cos²(α) = 1

Ossia:

sin²(α) = 1 - cos²(α)

L’equazione diventa:

a_T (M + m sin²(α)) = m g sin(α) cos(α)

E, infine:

a_T = m g sin(α) cos(α)/(M + m sin²(α)) …. (5)

Potremmo, adesso, inserire questo valore nella prima equazione della (4) e ricavare a_C. Ma possiamo anche continuare a eseguire qualche “trucchetto” sulla (4). Ad esempio, moltiplicare la prima equazione per cos(α) e la seconda per (M + m). Otteniamo:

(M + m) a_Tcos(α) - m a_C cos²(α) = 0

(M + m) a_C– (M + m) a_T cos(α) = (M + m)g sin(α)

Sommando le due equazione si elimina il termine in a_T:

- m a_C cos²(α) + (M + m) a_C = (M + m) g sin(α)

a_C (M + m – mcos²(α)) = (M + m) g sin(α)

a_C (M + m sin²(α)) = (M + m) g sin(α)

E, infine:

a_C = (M + m) g sin(α)/(M + m sin²(α)) …. (6)

Passiamo alla seconda parte del problema, ossia per quale valore di M/m il cuneo accelera di più del cubo?

a_T/a_C = (m g sin(α) cos(α)/(M + m sin²(α))) · ((M + m sin²(α))/(M + m) g sin(α))

a_T/a_C = m g sin(α) cos(α)/(M + m) g sin(α)

a_T/a_C = m cos(α)/(M + m)

cos(α) = ((M + m)/m) (a_T/a_C)

cos(α) = (M/m + 1)(a_T/a_C)

cos(a) deve essere minore di 1

M/m > 0

M/m + 1 > 1

a_T < a_C SEMPRE

Il cuneo non può mai accelerare di più del cubo

N.B.: Il grande lavoro svolto da Arturo e da Fabrizio hanno permesso un'analisi ben più dettagliata di questo problema sicuramente di grande interesse. Aspettatevi una trattazione ben più completa e articolata!

QUI le altre soluzioni

25 commenti

michele celenza

22/08/2019 at 17:18

Molto chiara la soluzione nonostante il procedimento assai lungo.

Scusa Vincenzo faccio una banale osservazione:

quando calcoli le F1 e F2

F1 (componente della forza peso del cubo lungo la direzione s)

F2 (componente lungo la direzione s della accelerazione subita dal cubo per il trascinamento verso sx)

se si considera come positivo il verso di s verso il basso

F1 = mg sin (α)

F2 = - m aT cos (α)

si sarebbe dovuto scrivere in luogo di F1 - F2 F1 + F2

(somma di vettori)

Con i tuoi aiuti ero riuscito ad applicare la conservazione della quantità di moto lungo la direzione x

ma il seguito è molto più complesso
Vincenzo Zappalà

22/08/2019 at 17:59

caro Michele,

il segno puoi metterlo come vuoi... l'importante è che le due componenti abbiano segno opposto. In altre parole, devi fare una differenza tra due vettori diretti in verso opposto se vuoi trovare la risultante: v1 - v2. Devi sommare due cose di segno opposto. Pensa di fare F1 + F2, ma ciascuna con il suo segno...

Sai, non è più complesso. Devi pensare all'unica componente dell'accelerazione che può agire sul moto e questa è g sen (alpha). Essa deve per forza essere uguale alla somma delle due componenti che derivano da F1 e F2. Una è proprio l'accelerazione aCs (di cui prima avevamo preso la componente lungo x) moltiplicata per m e l'altra è la componente di aT, moltiplicata solo per la massa m, lungo s. Due forze impartite al cubo che, alla fine, devono essere uguali all'unica forza agente su tutto il sistema. Pensa che il cubo da un lato scende, ma la sua discesa risente anche dello spostamento del cuneo. Va quindi tolta quest'ultima componente per trovare la forza reale.

In questo senso, ha fatto bene Arturo a separare sempre le due masse M e m fin dalla conservazione del momento. Forse risulta più chiaro...
Fabrizio

23/08/2019 at 00:46

Enzo, c'è qualcosa che non mi torna nelle conclusioni.

Tutto chiaro il procedimento per ricavare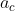 $a_c$ ed $a_T$ .

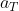Ciò che non mi torna è l'utilizzo di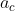 $a_c$ nel confronto con $a_T$ .

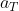Mentre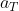 $a_T$ è l'accelerazione del cuneo nel sistema di riferimento "di laboratorio", 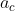$a_c$ mi sembra sia l'accelerazione del cubo nel sistema di riferimento solidale con il cuneo.

Due considerazionia a supporto.

Nel figura disegni il vettore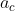 $a_c$ parallelo alla piano inclinato del cuneo. Questo è valido per l'accelerazione del cubo nel sistema di riferimento del cuneo. Nel sistema di riferimento "di laboratorio" l'accelerazione di m deve essere maggiormente inclinata per "compensare" il movimento del cuneo.

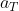Nella espressione (2), che metto nella forma $m (a_c cos(\alpha) - a_T)- M a_T =0$ , giustamente, attribuisci ad m una accelerazione che ha la componente orizzontale $(a_c cos(\alpha) - a_T)$ . Il - $a_T$ è proprio l'elemento che fa passare dal sistema di riferimento di 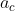$a_c$ , solidale con il cuneo, a quello di laboratorio.

Per fare il confronto tra le accelerazioni nel sistema di laboratorio devo trovare l'accelerazione totale del cubo nel sistema di laboratorio.

La componente orizzontale è quella vista sopra. La componente verticale non è modificata dal cambiamento di sistema di riferimento e rimane $a_c sin(\alpha)$ .

Quindi, il modulo quadrato della accelerazione del cubo nel sistema di riferimento di laboratorio è

$(a_c cos(\alpha) - a_T)^2+a_c^2 sin(\alpha)^2$ che devo confrontare con $a_T^2$

$\left [(a_c cos(\alpha) - a_T)^2+a_c^2 sin(\alpha)^2 \right ]-a_T^2=$ ${{a}_{c}}\left({{a}_{c}}- 2{{a}_{T}}\cos{\left( \mathit{\ensuremath{\alpha}}\right) }\right)>0$

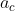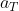Sostituendo con le espressioni di $a_c$ e $a_T$ che hai trovato si ottiene dopo qualche passaggio

$\frac{\left( \mathit{\frac{M}{m}}+1\right) \,{{g}^{2}}\,\left( \mathit{\frac{M}{m}}+1-2{{\cos{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}\right) \,{{\sin{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}}{{{\left( {{\sin{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}+\mathit{\frac{M}{m}}\right) }^{2}}}>0$

Che è lo stesso risultato che avevo ottenuto nella mia risposta per altra via.

(Nel sistema di riferimento di laboratorio) L'accelerazione totale del cubo è sempre maggiore di quella del cuneo per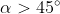 $\alpha>45^{\circ}$ .

Per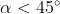 $\alpha<45^{\circ}$ , l'accelerazione totale del cubo è maggiore di quella del cuneo se $\frac{M}{n}>2\cos(\alpha)^2-1=\frac{1-\tan(\alpha )^2}{1+\tan(\alpha )^2}$
Vincenzo Zappalà

23/08/2019 at 07:10

Scusa Fabrizio,

ma non si cambia sistema... la stessa accelerazione che subisce il cubo sopra il cuneo, nella prima equazione, deve essere considerata nella seconda, dove si eguaglia il tutto all'unica forza fisica agente sull'intero sistema. In tal modo l'accelerazione lungo s viene calcolata tenendo conto dei contributi dati dal movimento del cuneo e la loro reazione. Forse non mi sono spiegato bene, ma il movimento finale e quindi le accelerazioni finali devono essere quella del cuneo lungo x e quella del cubo lungo s.

Se considerassi solo lo scivolamento del cubo a se stante, nel sistema cuneo fermo, troverei che la sua accelerazione è g sen(alpha) e basta.

A parte le componenti secondo vari assi, è indubbio che il cubo può solo mostrare un'accelerazione lungo s e il cubo una lungo x. Che poi queste abbiano componenti non nulle secondo gli altri assi serve per risolvere il sistema in due incognite.

Forse vediamo il problema sotto un aspetto diverso...
Fabrizio

23/08/2019 at 09:51

Si, probabilmente stiamo vedendo il problema sotto aspetti diversi, anche se penso che alla fine dovrebbero convergere nel risultato.
Un punto può essere che il confronto lo penso tra le accelerazioni del cuneo e del cubo nel sistema di riferimento fisso (quello nel quale cuneo e cubo sono inizialmente fermi). Ma non credo che sia qui il modo diverso di vedere il problema.

In questo sistema di riferimento posso applicare la legge di Newton che scrivo utilizzando per le accelerazioni caratteri maisculi per distinguerli da quelli finora utilizzati. In particolare le componenti orizzontali di forza ed accelerazione sono legati dalla relazione: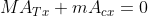 $M A_T_x+m A_c_x=0$ .

Confrontata con la (2), $m (a_c cos(\alpha) - a_T)- M a_T =0$ , che credo valida, risulta che $A_T_x=a_T\; e\; A_c_x= (a_c cos(\alpha) - a_T)$ . La differenza di segno deriva solo dall'orientamento dei vettori.

Da qui si vede che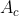 $A_c$ non può essere uguale ad 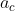$a_c$ poiché hanno componenti orizzontali diverse. Non ripeto i passaggi per ottenere il modulo di 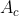$A_c$ che sono nel precedente commento.

In effetti l'accelerazione del cubo (nel riferimento fisso) non è lungo s, se lungo s si intende un piano di pendenza $\alpha$ . Proprio per rimanere appoggiato su s, il cubo segue una traiettoria con pendenza maggiore di $\alpha$ (nel riferimento fisso). La figura non è una simulazione, ma penso rappresenti la situazione.

Se la traiettoria ha pendenza costante maggiore di $\alpha$ anche l'accelerazione deve avere la stessa pendenza maggiore di $\alpha$ .

Spero di avere rappresentato il mio punto di vista.
Vincenzo Zappalà

23/08/2019 at 10:17

Interessante... sicuramente. Però non mi convince il fatto che alla fine l'accelerazione del cubo non sia gsin(alpha).

Forse potresti avere ragione pensando a due accelerazioni riportate in due sistemi diversi...ma non ne sono completamente convinto perché tutto il sistema deve muoversi solo per la forza di gravità.

Vediamo se Arturo o qualcun altro ci aiuta a risolvere il dilemma. Questo è il bello della condivisione...
Arturo Lorenzo

23/08/2019 at 11:17
Io direi che stiamo dicendo le stesse cose ma inquadrandole da punti di vista differenti.

Prendiamo le espressioni trovate per le accelerazioni, sia nella soluzione di Enzo sia nei commenti al quiz. Non le riscrivo per brevità, mi interessa qui indicarne solo il simbolo e il significato:

aC (quella che io ho chiamato "a" nel mio commento al quiz) = modulo dell'accelerazione totale (composizione delle due componenti x e y) del cubo nel sistema di riferimento del cuneo (quindi sistema non inerziale)

aT (quella che io ho chiamato aMx nel mio commento al quiz)= modulo dell'accelerazione totale (coincidente con la sola componente x) del cuneo nel sistema di riferimento inerziale

amx e amy (da me ricavate nel mio commento al quiz) = moduli delle componenti dell'accelerazione del cubo nel sistema di riferimento inerziale

Ebbene, servendomi di un foglio Excel per evitare di fare ogni volta gli stessi conti, ho verificato che con le suddette espressioni delle accelerazioni:

(1) Confrontando l'accelerazione del cuneo in SRI con l'accelerazione totale del cubo in SRI:
- per alfa < 45° l'accelerazione totale del cubo è > di quella del cuneo quando la massa del cuneo M è maggiore di quella del cuneo esattamente della quantità indicata da Fabrizio nel suo commento
- per alfa >45° l'accelerazione totale del cubo è > di quella del cuneo per qualsiasi valore delle masse
(2) Confrontando l'accelerazione del cuneo in SRI con l'accelerazione totale del cubo nel sistema non inerziale, cioè quello solidale al cuneo che accelera verso sinistra:
- l'accelerazione totale del cubo è sempre > di quella del cuneo, a prescindere dall'angolo alfa e dal valore delle masse, come indicato dall'espressione riportata in soluzione e nel mio commento
(3) Confrontando l'accelerazione del cuneo in SRI con la sola componente orizzontale del cubo in SRI dell'accelerazione totale del cuneo:
- la componente orizzontale dell'accelerazione del cubo è maggiore di quella del cuneo se M>m (come da me indicato nel commento
Quanto sopra , limitatamente al punto 3 (ma credo si possa verificare anche il punto 1), è stato da me verificato con una simulazione con Algodoo, con cui avevo realizzato l'animazione visibile qui.

In definitiva, dipende da cosa confrontiamo e in base a quale sistema di riferimento.
Vincenzo Zappalà

23/08/2019 at 11:39

sembra tutto molto logico, ma rimango dell'idea che la soluzione data da me e quella di Arturo rappresentino la situazione in un sistema esterno. La soluzione per l'accelerazione del cubo tiene conto del movimento del cuneo con lui sopra verso sinistra e non si riferisce solo al sistema in movimento giudicato fermo. Sono convinto che la strana accelerazione di Fabrizio (apparentemente coerente) possa separarsi nelle due componenti che abbiamo dato noi.
Arturo Lorenzo

23/08/2019 at 15:35

Ho avuto modo di verificare con Algodoo anche il caso (1), e risulta confermato anche quello.

Ho considerato alfa=30° (quindi < 45°) e ho "misurato" le accelerazioni di cuneo e cubo, entrambe in SRI. Per alfa = 30°, il fattore con le tangenti al quadrato presente nelle formule riportate da Fabrizio vale 0,5. Ho posto la massa m del cubo pari a 10kg e ho vatto variare quella del cuneo da un valore 4 kg a un valore 6 kg, passando quindi per il valore intermedio di 5 kg. Allego tre fermi-immagine:

In questo caso l'accelerazione del cubo (indicata in alto a destra dalla freccetta rossa) risulta minore di quella del cuneo (indicata dalla freccetta rossa al centro della figura)

In questo caso l'accelerazione del cubo risulta uguale a quella del cuneo.

Infine, in questo caso, l'accelerazione del cubo risulta maggiore di quella del cuneo.

Purtroppo, che io sappia, non è possibile "misurare" con Algodoo le accelerazioni nel sistema non inerziale. Ma non c'è motivo di dubitare , come dicevo nel precedente commento, tutto è in perfetto accordo, basta specificare cosa confrontiamo e rispetto a quale sistema di riferimento.
Vincenzo Zappalà

23/08/2019 at 15:56

Scusa Arturo,

ma l'accelerazione del cubo nel sistema di riferimento del cuneo (considerato fermo) sarebbe solo quella dovuta alla gravità... aC = gsen(alpha). Mi sa che continuiamo a dire le stesse cose, ma non riesco a capire la vera differenza...
Arturo Lorenzo

23/08/2019 at 16:29

Immagino di trovarmi sopra il cuneo e di godermi la scena... :-)

Se l'accelerazione del cubo per me fosse solo quella dovuta alla gravità, non mi tornerebbero i conti. Perché vedrei scivolare il cubo più velocemente di quanto avviene nel caso di cuneo fermo. Alla accelerazione dovuta alla gravità , per spiegarmi il fenomeno e far quadrare i conti, dovrei aggiungere una accelerazione dovuta alla forza apparente verso destra , per il fatto che il sistema da cui osservo non è inerziale ma uniformemente accelerato verso sinistra. Questo è, credo, il motivo per cui poi l'accelerazione totale del cubo nel sistema del cuneo risulta sempre maggiore di quella del cuneo.
Fabrizio

23/08/2019 at 16:30

Scusa Arturo,
dal telefonino non riesco a leggere i valori delle accelerazioni per confrontarli con quelli delle formule.
Nel caso di m=4kg, secondo le formule, l'accelerazione del cuneo dovrebbe essere circa 42.43 e quella totale del cubo 38.27.
Arturo Lorenzo

23/08/2019 at 16:40

Fabrizio, nella mia simulazione, m è sempre = 10 kg. Ho fatto variare M, da 4 a 6 kg. Angolo sempre di 30°.

Per m=10kg, M=4 kg, ottengo, sia dalle formule sia dalla simulazione:

am (accelerazione totale del cubo nel SRI) = 5,89 m/s^2

aMx (accelerazione del cuneo nel SRI) = 6,53 m/s^2

[ credo che , con riferimento ai valori da te riportati , ti sia dimenticato di dividerli per (M+m sin^2(alfa) ) ]
Vincenzo Zappalà

23/08/2019 at 17:06

cari amici,

penso che alla fine abbiamo tutti ragione... probabilmente come diceva Arturo. Ho trovato la soluzione per le accelerazioni in un yuotube e sembra che tutto torni... Oltretutto, la parte finale è decisamente molto istruttiva.

Beh... ci siamo divertiti direi e siete stati veramente bravi... C'è sempre da imparare qualcosa!

https://www.youtube.com/watch?v=xuXwWjbnVPg

Ovviamente, lasciamo perdere la frizione....
Arturo Lorenzo

23/08/2019 at 17:16

Ciliegina sulla torta...

L'angolo, rispetto alla direzione orizzontale , dell'accelerazione totale del cubo nel SRI è dato da (ci si arriva dalle componenti lungo x e lungo y:

$\beta = arctan[ \frac{M+m}{m}*tan(\alpha)]$

cioé:

$\beta =arctan[](1+\frac{m}{M})*tan(\alpha )]$

da cui si vede che , per M>>m, l'angolo $\beta$ tende a coincidere con l'angolo $\alpha$ . Infatti, per M>>m il cuneo sarà praticamente fermo, e quindi il sistema SRI coinciderà con quello del cuneo, e l'accelerazione del cubo tornerà ad essere parallela al piano di scivolamento
Vincenzo Zappalà

23/08/2019 at 17:33

Bene, bene... tutto torna... ora ne sono convinto in pieno!
Fabrizio

24/08/2019 at 01:58

Visto che c'è stata una analisi approfondita di questo problema, ho pensato di proporre anche un procedimento che utilizza il metodo di Lagrange. Una introduzione al metodo di Lagrange è in archivio qui.

Nel metodo di Lagrange, per prima cosa occorre scegliere le coordinate che useremo per descrivere e risolvere il problema. Il numero di coordinate deve essere il minimo indispensabile per descrivere il moto degli elementi del sistema. La scelta delle coordinate è notevolmente arbitraria. Questo ci da modo di scegliere le coordinate che semplificano la trattazione del problema. In pratica è l'unica scelta che dobbiamo fare, il resto va quasi in automatico.

Nel nostro caso il numero di coordinate da individuare è 2. Il cuneo M si muove lungo una retta orizzontale ed il moto può essere descritto da una coordinata orizzontale rettilinea che chiamo q. Per comodità oriento la coordinata verso sinistra e metto l'origine nel punto dove il cubo m viene rilasciato. Il cubo m si muove sia orizzontalmente sia verticalmente, ma i due movimenti sono legati tra loro dal vincolo di trovarsi sul piano inlinato del cuneo. Posso descrivere il suo movimento con una sola coordinata rettilinea orizzontale che vincola anche la sua posizione verticale. La scelgo in un modo apparentemente strano. Immaginiamo di fare una tacca sul cuneo nel punto dove si trovava inizialmente il cubo, ovviamente la tacca si muove con il cuneo. La coordinata che scelgo è la distanza tra questa tacca e la posizione orizzontale del cubo. Per comodità la oriento verso destra. Chiamo S questa coordinata. Per come è impostato il problema non servono altre coordinate perchè non ci sono movimenti lungo la profondità del disegno.

Da notare che lo spostamento orizzontale del cubo è S-q, mentre lo spostamento verticale del cubo è $-S \tan(\alpha )$ . La strana scelta della coordinata S è fatta proprio per fa dipendere lo spostamento verticale del cubo da una sola coordinata.

Da qui il processo è quasi automatico.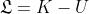
Ora posso trovare la Lagrangiana. La definizione della Lagrangiana è l'energia cinetica del sistema meno l'energia potenziale, $\mathfrak{L}=K-U$ .

L'energia cinetica dipende dal quadrato della velocità del cubo e del cuneo espresse con le coordinate scelte. La prima coordinata, q, è proprio la posizione del cuneo. La velocità del cuneo è la derivata rispetto a tempo di questa coordinata. La scrivo con la notazione compatta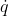 $\dot{q}$ ed il quadrato è $\dot{q}^2$ .

Il cubo si muove orizzontalmente e verticalmente. Abbiamo visto sopra che lo spostamento orizzontale è S-q e lo spostamento verticale è $-S \tan(\alpha )$ . Le due velocità corrispondenti sono quindi $\dot{S}-\dot{q}\;\;\;e\; -\dot{S}\tan(\alpha)$ $\dot{S}-\dot{q}\;\;\;e\; -\dot{S}\tan(\alpha)$ . Il quadrato della velocità del cubo è quindi $(\dot{S}-\dot{q})^2+\dot{S}^2\tan(\alpha)^2$ (teorema di Pitagora).

L'energia cinetica complessiva è $\frac{1}{2}M\,\dot{q}^2+\frac{1}{2}m\left [(\dot{S}-\dot{q})^2+\dot{S}^2\tan(\alpha)^2 \right ]$

L'energia potenziale dipende dalla posizione verticale del cubo: $U=m g (-S\, tan(\alpha))$ .
Mettendo insieme i due addendi otteniamo la Lagrangiana

$\mathfrak{L}=\frac{1}{2}M\,\dot{q}^2+\frac{1}{2}m\left [(\dot{S}-\dot{q})^2+\dot{S}^2\tan(\alpha)^2 \right ]+m\,g\,S\,\tan(\alpha)$

Per ottenere le equazioni del moto si applica l'equazione di Eulero-Lagrange alla Lagrangiana per ciascuna variabile.
$\left\{\begin{matrix} \frac{\mathrm{d} }{\mathrm{d} t}\frac{\partial }{\partial \dot{q}}\mathfrak{L}-\frac{\partial \mathfrak{L}}{\partial q}=0\\ \frac{\mathrm{d} }{\mathrm{d} t}\frac{\partial }{\partial \dot{S}}\mathfrak{L}-\frac{\partial \mathfrak{L}}{\partial S}=0 \end{matrix}\right.$

procedendo con le derivate

$\left\{\begin{matrix} M\,\frac{d}{dt}{\dot{q}} -m\, \frac{d}{dt}\left({\dot{S}-\dot{q}}\right) =0\\ m\,\left(\frac{d\dot{S}}{dt} \tan(\alpha)^2+\frac{d}{dt}{\left( \dot{S}-\dot{q}\right)} \right)-g\, m\,\tan(\alpha)=0 \end{matrix}\right.$

$\left\{\begin{matrix} M\,{\ddot{q}} -m\, \left({\ddot{S}-\ddot{q}}\right) =0 \\ m\,\left(\ddot{S} \tan(\alpha)^2+\ddot{S}-\ddot{q}\right) \right)-g\, m\,\tan(\alpha)=0 \end{matrix}\right.$

$\left\{\begin{matrix} (M+m)\,{\ddot{q}} -m\, \ddot{S} =0\\ (\tan(\alpha)^2+1)\ddot{S} -\ddot{q} \right)=g\, \tan(\alpha) \end{matrix}\right$

Corrispondono esattamente alle equazioni (2) e (4) di Enzo, qui trovate direttamente per via analitica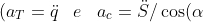 $(a_T=\ddot{q}\;\;\; e \;\;\; a_c=\ddot{S}/\cos(\alpha))$

Si tratta di un sistema di due equazioni con incognite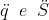 $\ddot{q}\;\; e \;\;\ddot{S}$ . La procedura di soluzione è simile a quella descritta da Enzo ed il risultato è

$\left\{\begin{matrix} \ddot{q}=\frac{gm\,\tan{\left( \mathit{\ensuremath{\alpha}}\right) }}{M\,\left( {{\tan{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}+1\right) +m\,{{\tan{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}}=\frac{gm\,\cos{\left( \mathit{\ensuremath{\alpha}}\right) }\,\sin{\left( \mathit{\ensuremath{\alpha}}\right) }}{m\,{{\sin{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}+M}\\ \ddot{S}=\frac{g\,\left( m+M\right) \,\tan{\left( \mathit{\ensuremath{\alpha}}\right) }}{M\,\left( {{\tan{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}+1\right) +m\,{{\tan{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}}=\frac{\left( gm+Mg\right) \,\cos{\left( \mathit{\ensuremath{\alpha}}\right) }\,\sin{\left( \mathit{\ensuremath{\alpha}}\right) }}{m\,{{\sin{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}+M} \end{matrix}\right.$

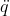Per quanto detto sopra, l'accelerazione del cuneo $(A_T)$ è orizzontale è corrisponde a $\ddot{q}$ .

La componente orizzontale dell'accelerazione del cubo $(A_C_x)$ è $\ddot{S}-\ddot{q}$ , mentre la componente verticale dell'accelerazione del cubo $(A_C_z)$ è $-\ddot{S}\,\tan(\alpha)$ .

$\left\{\begin{matrix} A_T=\frac{gm\,\cos{\left( \mathit{\ensuremath{\alpha}}\right) }\,\sin{\left( \mathit{\ensuremath{\alpha}}\right) }}{m\,{{\sin{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}+M}\\ A_C_x= \frac{g\,M\,\cos{\left( \mathit{\ensuremath{\alpha}}\right) }\,\sin{\left( \mathit{\ensuremath{\alpha}}\right) }}{m\,{{\sin{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}+M}\\ A_C_z=-\frac{\left( gm+Mg\right) \,\,\sin{\left( \mathit{\ensuremath{\alpha}}\right)^2 }}{m\,{{\sin{\left( \mathit{\ensuremath{\alpha}}\right) }}^{2}}+M}\\ \end{matrix}\right.$
Vincenzo Zappalà

24/08/2019 at 07:31

caro Fabrizio e Arturo,

Perché non mettete "in bella" le soluzioni con la lagrangiana e quella che utilizza la normale N? Potremmo aggiungerle alla soluzione data da me e -magari- inserire il caso interessante della forza F che spinge il cuneo verso destra e che studia quando il cubo si ferma e quando va addirittura in alto (vedi ultima parte di youtube).

Io andrò via per quattro giorni (da domani a mercoledì compresi) e probabilmente non avrò linea...

Prendetevi il tempo che volete... ma penso che il problema in generale sia estremamente istruttivo con tutte le sue possibili variazioni e conclusioni. Lo metteremo in archivio come applicazione di dinamica, con i tre nomi.Non ditemi di no....
MarcoC

11/09/2019 at 17:14

Nella soluzione è riportato che:

"Quanto vale la quantità di moto lungo quest’asse durante la discesa del cubo? Beh… vi è una parte dovuta allo spostamento del cubo verso destra che deve essere controbilanciata da quella del cuneo (la cui massa è però M + m, dato che si porta dietro anche il cubo) verso sinistra, in modo da dare come risultato ZERO."

Non riesco a capire perchè il cuneo si porta dietro anche il cubo, dato che i corpi non sono legati tra loro e non esiste alcuna forza d'attrito.

Grazie in anticipo per l'eventuale chiarimento.
Vincenzo Zappalà

11/09/2019 at 17:25

Caro MarcoC,

Sarebbe ben più difficile capire come potrebbe non portarselo dietro... Ricordiamoci che la forza di gravità esiste e il cubo viene spinto verso il basso anche durante il moto del cuneo, rimanendone così ancorato. Tutto ciò che può fare è scivolare su di esso.
MarcoC

12/09/2019 at 11:59

Si ok, questo era chiaro.

Forse nel post precedente mi sono espresso male.

Intendevo dire che non mi è chiaro perchè nella eq (2)

(M + m) aT - m aC cos(α) = 0 …. (2)

il coeff di aT è (M + m)

Io avrei scritto solo

M aT - m aC cos(α) = 0

Ecco, è questo il punto che non mi torna.

Grazie.
Vincenzo Zappalà

12/09/2019 at 12:07

caro MarcoC,

ma il cuneo che si muove verso sinistra DEVE portarsi dietro anche il cubo, per quello che si è detto prima, e quindi la massa deve essere la somma delle due. Verso destra, invece, si muove solo il cubo, mentre scivola sul cuneo e noi prendiamo solo la sua componente orizzontale per uguagliare la quantità di moto : all'inizio è tutto fermo.
MarcoC

12/09/2019 at 14:34

Continua a sfuggirmi qualcosa........

Provo a riassumere:

"ma il cuneo che si muove verso sinistra DEVE portarsi dietro anche il cubo, per quello che si è detto prima"

cioè perchè:

"Ricordiamoci che la forza di gravità esiste e il cubo viene spinto verso il basso anche durante il moto del cuneo, rimanendone così ancorato. Tutto ciò che può fare è scivolare su di esso."

Se il sistema di riferimento è fissato sul piano orizzontale, il cuneo si muoverà solo verso sinistra mentre il cubo, scivolando sul piano inclinato, si muoverà sia verso il basso sia verso destra. Come può il cubo andare anche verso sinistra?

Grazie.
Vincenzo Zappalà

12/09/2019 at 15:55

Dunque... nel sistema di riferimento solidale con il cuneo, il cubo si muove solo verso destra. Ma in un riferimento esterno, il cubo si muove sia verso sinistra con il cuneo, sia verso destra rispetto al cuneo. Il suo movimento visto dall'esterno tiene conto di entrambi. Provo a fare una figura con le posizioni in tempi diversi...

lo spostamento del cubo rispetto a un asse fisso è quello rosso che deriva dallo spostamento lungo il cuneo meno lo spostamento del cuneo (più il cubo)
MarcoC

12/09/2019 at 18:38

La ringrazio per l'ulteriore spiegazione e soprattutto per la figura a corredo, tuttavia non riesco ancora a "digerire" il concetto.

Proverò con altri quiz, che sicuramente potranno darmi altri spunti di riflessione.

Grazie.

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.

Soluzione (parziale) del quiz sul cuneo e il cubo ****

Articoli correlati

Due navi in mare aperto (*/**)

Sovrapposizione di stati: non solo gatti **

(Q) Velocità costante **/***

HENRY CAVENDISH

25 commenti

Lascia un commento Cancel Reply

(Q) Velocità costante /*