Quiz dinamico: quando si rompe? **
Un semplice problema che ci permette di lavorare con la tensione di una corda. Un granello in più nella conoscenza della meccanica classica.
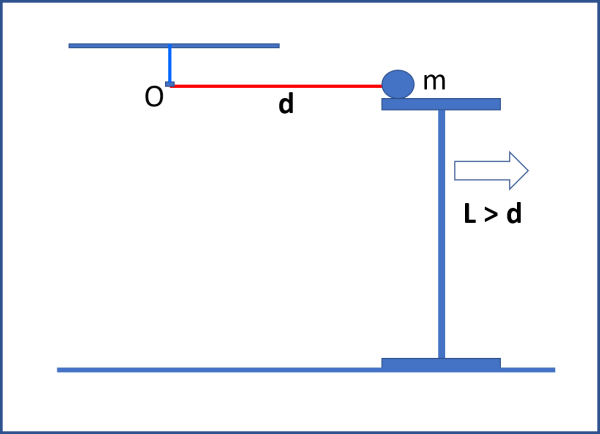
Un capo di una corda inestensibile di lunghezza d è fissato saldamente al soffitto. All'altro capo è fissata, altrettanto saldamente, una pallina di metallo di massa m. Attraverso un sostegno di altezza L > d, poniamo la pallina a un'altezza tale che la corda risulti perfettamente tesa e orizzontale.
Con un gesto rapidissimo togliamo il sostegno e ci chiediamo:
Quanto deve essere resistente la corda affinché non si rompa e la pallina cada al suolo?






4 commenti
Provo ad imbastire una soluzione:
la massima forza che la corda dovrà sostenere è quando la massa si trova sulla verticale perchè è proprio in quel punto che la forza centripeta sarà massima.
Facendo i calcoli:
Fc=m*ac
ac=1/d*V^2
mgd=1/2mv^2
da cui
Fc=m*2g
oltre a questa forza, la corda dovrà sostenere anche la forza peso della massa.
Quindi in conclusione dovrebbe essere:
Ftot=Fc+Fg=m*2g+mg=3mg
grazie MarcoC... attendiamo qualche altro coraggioso...
Si consideri il riferimento x0y :
asse y d in posizione verticale passante per il punto O di sospensione
asse x perpendicolare ad y (d) in "basso" rispetto al punto di sospensione
la massa m è vincolata a percorrere la traiettoria semicircolare di raggio d
applicando il principio di conservazione dell'energia meccanica:
E = T + U
nella posizione di partenza si abbiamo la massima energia di posizione U (riferita al sistema considerato) ed energia cinetica T nulla:
E = 0 + U
E = 0 + mg d
nella posizione verticale in "basso" si ha la massima velocita della massa m e la massima energia cinetica T ed energia di posizione nulla
E = T + 0
E = 1/2 m v2 + 0
dovendo conservarsi l'energia meccanica totale si ha
mg d = 1/2 m v2
v2 = 2 g d
v =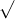 2g d
2g d
per la rotazione intorno al punto di sospensione O la massa m è soggetta ala accelerazione centripeta
ac = v2/d
ed alla forza centripeta
Fc = m ac
Fc = m v2/d
Fc = 2 m g d/d
Fc = 2 m g
nella posizione in basso la massa m oltre alla forza centripeta è soggetta alla forza peso quindi la forza di tensione totale a cui è soggetto il filo d è
F = Fc +Fp
F = 2mg + mg = 3 mg
quindi la resistenza R del filo d deve esse maggiore di F = 3 mg
R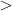 3 mg
3 mg
grazie Michele...