Categorie: Fisica Fisica classica
Tags: costante elastica fisica fisica classica molla quiz urto urto anelastico
Scritto da: Arturo Lorenzo
Commenti:12
Un urto... ammortizzato ***
Urto.... con ammortizzatore
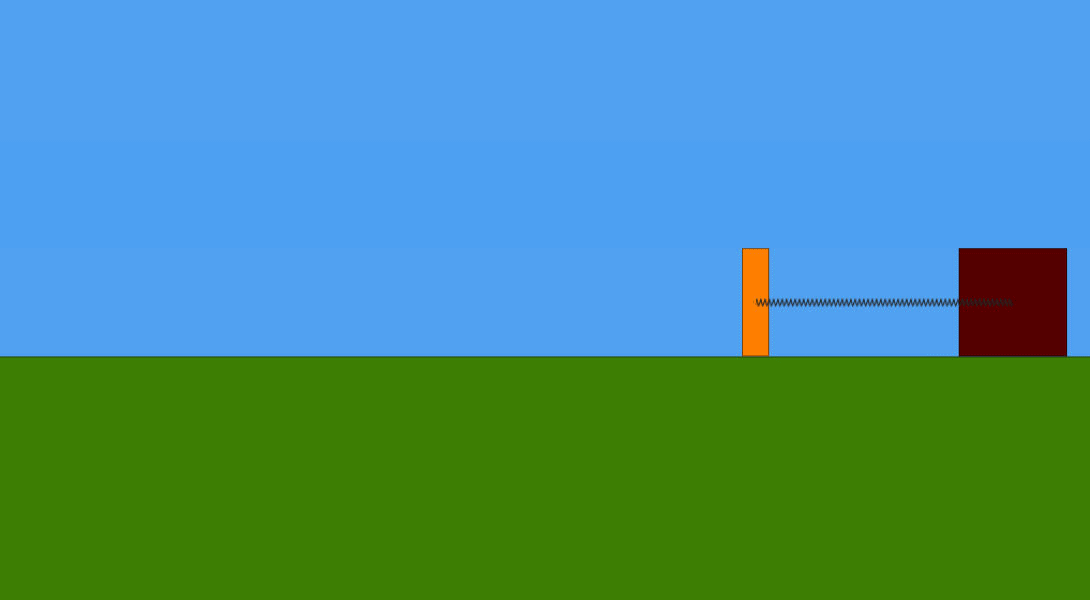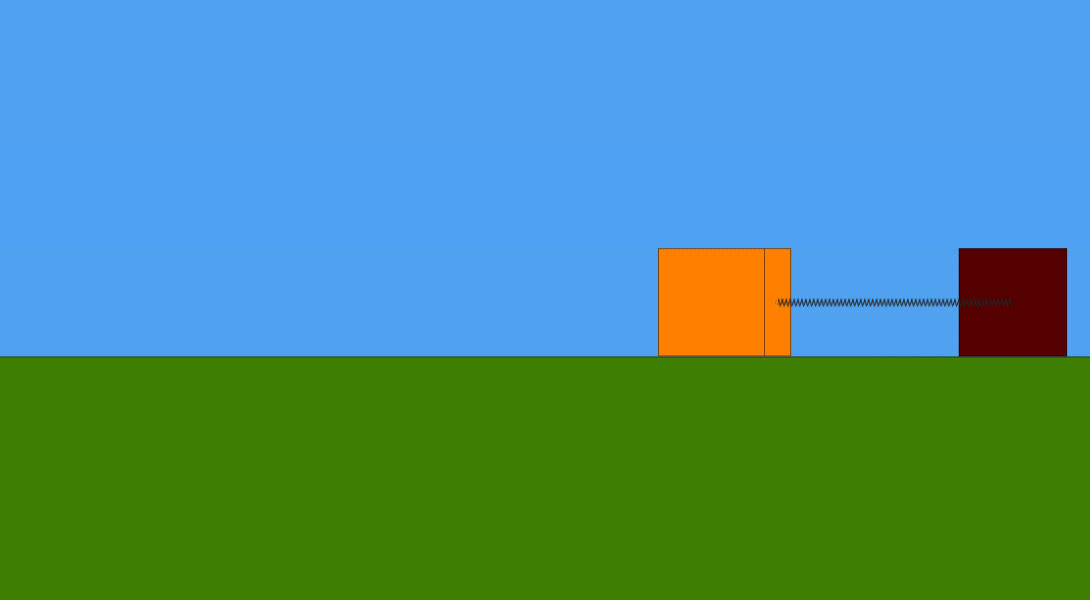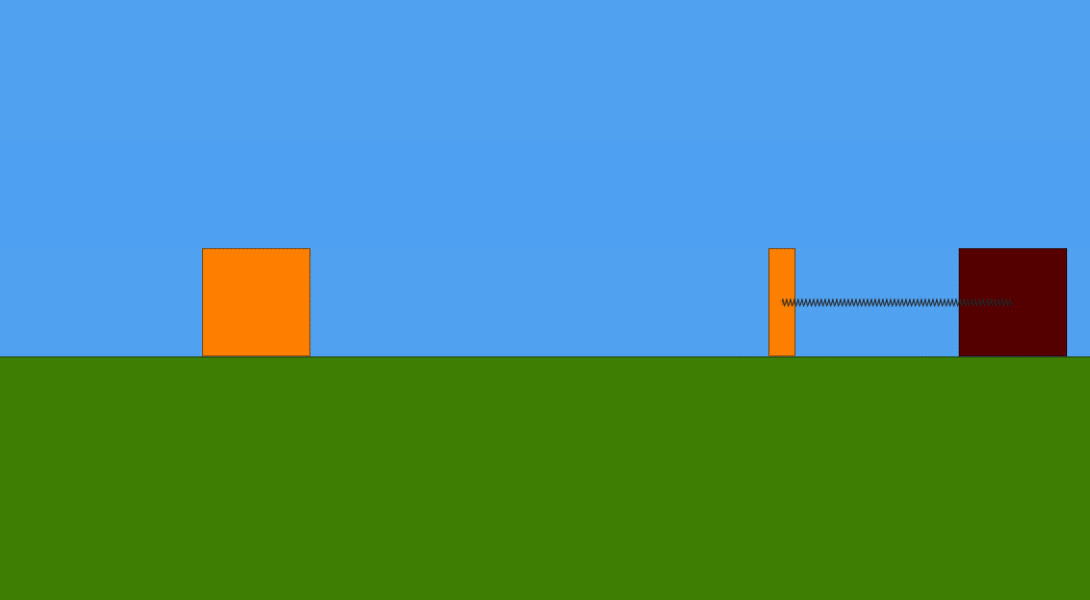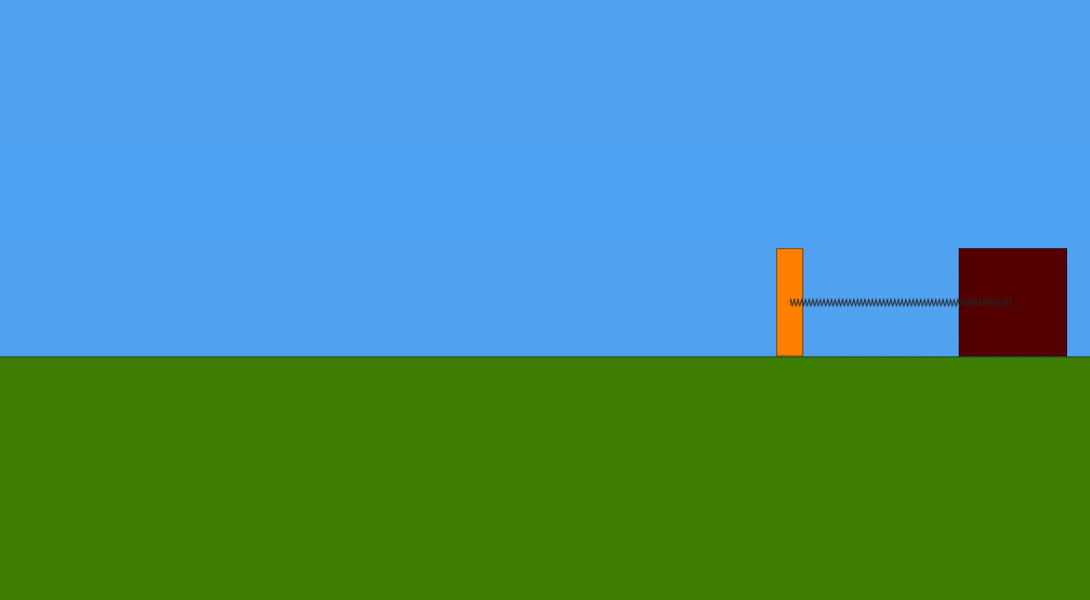
Abbiamo una massa m1 che scorre senza attrito con velocità v1 lungo un piano orizzontale verso una seconda massa m2. Quest'ultima è inizialmente ferma ed è collegata all'estremità sinistra di una molla ideale di costante elastica k , a sua volta fissata, nella sua estremità destra, ad un blocco inamovibile. Inevitabilmente, ad un certo punto la massa m1 urterà la massa m2. L'urto tra le due masse è da considerare perfettamente anelastico. Infatti, dopo l'urto, le due masse procedono insieme verso destra. Ma subentra la forza elastica della molla , che, venendo compressa, le rallenta fino a fermarle, per poi cominciare a spingerle e farle muovere nel verso opposto. Si intuisce che , proseguendo ora verso sinistra, ad un certo punto la massa m1 si separerà dalla massa m2 e continuerà a muoversi di moto rettilineo uniforme verso sinistra. La massa m2, invece, comincerà ad oscillare avanti e indietro attorno alla sua posizione di equilibrio. Tutto si vede bene nella seguente animazione.
Si chiede di:
a) calcolare il massimo spostamento delle due masse dalla posizione in cui si trovava inizialmente ferma la massa m2
b) calcolare la velocità con cui la massa m1 si muoverà verso sinistra dopo essersi separata dalla massa m2
c) calcolare lo spostamento massimo della massa m2 dalla sua posizione di equilibrio, successivamente al momento in cui le due masse si separano dopo l'urto
d) calcolare il periodo di oscillazione della massa m2
Buon divertimento :-)
12 commenti
Aiutino
L'energia potenziale elastica di una molla è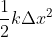
, dove con 
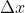ho indicato l'"elongazione", cioè la differenza tra la nuova lunghezza raggiunta dalla molla e la sua lunghezza a riposo, e con k la costante elastica della molla.
Precisazione: nell'urto tra la massa m1 e la massa m2 non vi è alcun "accartocciamento" tra le due. Semplicemente , nell'istante in cui si toccano prendono a muoversi insieme verso destra con una stessa velocità.
Provo ad imbastire una soluzione.
a)
la forza elastica è conservativa quindi tutta l’energia cinetica iniziale si trasformerà in energia potenziale quindi
1/2m1v1^2 = 1/2kx^2
risolvendo rispetto ad x ottengo la massima elongazione
b)
quando la molla respinge le due masse, nell'istante in cui transita nel suo punto di riposo (elongazione pari a 0), tutta l’energia potenziale sarà restituita alle due masse sotto forma di energia cinetica quindi
1/2kx^2=1/2(m1+m2)vf^2
risolvendo rispetto a vf ottengo la velocità con cui m1 si muove verso sinistra dopo essersi separata da m2
c)
dopo la separazione la massa m2 trasferirà alla molla tutta la sua energia cinetica quindi
1/2m2vf^2=1/2kl^2
risolvendo rispetto ad l ottengo la nuova massima elongazione della molla con agganciata solo m2
d)
il periodo di oscillazione della molla con agganciata la massa m2 dipende solo da m2 e k e non dalle condizioni iniziali dell'oscillazione
Spero di non aver scritto (troppe) eresie........
Intanto, grazie, Marco.
Iniziando dalla risposta alla domanda a), da essa sembrerebbe che la massa m2 si muova, immediatamente dopo l'urto con la massa m1, con la stessa velocità iniziale di quest'ultima. Qualcosa non quadra...
La quantità di moto si conserva immediatamente prima del contatto con la molla quindi
m1v1=(m1+m2)V
allora forse
1/2(m1+m2)V^2=1/2kx^2
Non ho capito l accartocciamento ma se è anelastico si conserva solo la quantita di moto mentre l energia cinetica diminuisce.
Dalla conservazione della q si ricava la velocità dopo l urto. Dalla velocità dopo l urto si calcola l energia cinetica , da cui la compressione della molla. Molto semplice.
Leandro: la precisazione era finalizzata ad escludere dissipazioni di energia per accartocciamento e a garantire alla massa m1 di separarsi dalla m2 nella fase successiva.
Marco (ma vale per tutti): per la domanda d) riusciamo a scrivere la formula che restituisce il periodo ?
m2 oscillerà intorno alla posizione di riposo l0 secondo la seguente equazione di moto
F2=m2*a=-k*(x(t)-l0)
Scegliendo opportunamente la x0 in l0, e definendo ω ^2=k/m2, si vede che
x(t)=α *sin(ω *t)
v(t)=α *ω *cos(ω *t)
a(t)=-α *ω ^2*sin(ω *t)
α lo determino considerando le condizioni iniziali al tempo t=0 in cui m1 si distacca da m2
x(0)=l0=0
v(0)=vi1
a(0)=0
Sostituendo risulta:
α =-v1*m1/(m1+m2)*rad(m2/k)
Se grafico x(ωt) sulle ordinate in funzione di ωt (sulle ascisse):
è come il seno di ωt con un'ampiezza pari a α .
Ogni periodo 2π (in ωt) torno nella medesima condizione di x e v.
Quindi il periodo T (in t soltanto) è pari a 2π/ω =2π *rad(m2/k)
Sì, io avrei scritto la stessa formula già scritta da Francesco
T=2π*sqrt(m2/k)
Francesco:
"Scegliendo opportunamente la x0 in l0, e definendo ω ^2=k/m2, si vede che
x(t)=α *sin(ω *t)"
Sarebbe più corretto dire "si dimostra" (e dimostrarlo) , ma alla fine il risultato è quello. Vedremo di approfondire il discorso nella soluzione.
Premesso la legge di newton, ove il doppio punto è la derivata seconda ed x è lo spazio,
comunemente, per abbreviare i calcoli, si applica Laplace
da cui semplicemente
e, antitrasformando
che è un bellissimo moto armonico senza smorzamento .....
manca il tempo e eh eh