Categorie: Matematica
Tags: circonferenza corde geometria quiz raggio
Scritto da: Vincenzo Zappalà
Commenti:18
Quiz geometrico: il raggio di un cerchio **
Mentre i più bravi stanno lottando con la molla di Arturo, lasciatemi proporre un semplice (ma non banalissimo) quiz geometrico. Da domani mi prenderò una settimana di ferie rilassanti (soprattutto alla ricerca di funghi) e penso di connettermi poche volte (tutto dipende dai ... funghi). Insomma, ce n'è per tutti i gusti.
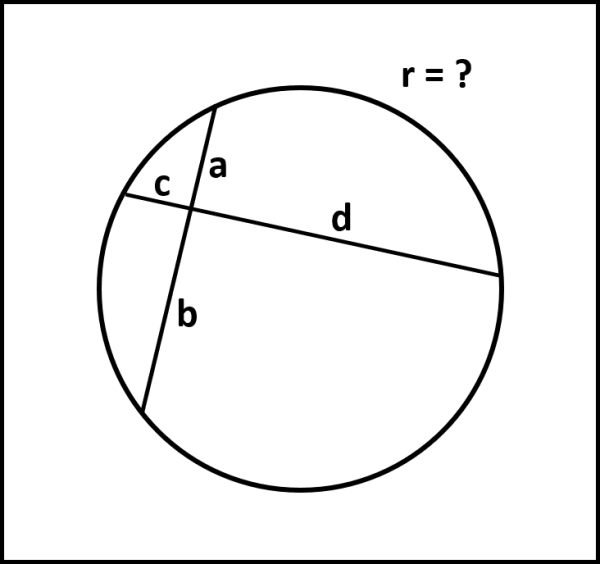
Prendiamo una bella circonferenza e tracciamo a caso due corde perpendicolari tra loro. La loro intersezione le divide in quattro segmenti: a,b,c,d.
Domanda: Trovare la più immediata e semplice relazione che lega il raggio della circonferenza ai quattro segmenti.






18 commenti
Se assommi li quadrati di a assommato a b e di c dedotto da d oterrai quatro volte lo raggio quadrato.
r=sqr(a^2 +b^2+c^2+d^2)
diviso 4 sotto radice.
me lo dimostrate?
area cerchio=somma 4 aree se sposto segmenti passanti per il centro circonferenza le 4 aree sono calcolabili perché r=a=b=c=d
r=1/2sqr(a^2+b^2+c^2+d^2)
Scrivo una dimostrazione incompleta.
a^2+d^2=(2r*senα/2)^2
dove con alfa indico l'angolo al centro che sottende l'ipotenusa AD
c^2+b^2=(2r*senβ/2)^2
dove con beta indico l'angolo al centro che sottende l'ipotenusa CB
sommando membro ottengo
a^2+b^2+c^2+d^2=4r^2 * [ sen^2(α/2) + sen^2(β/2) ]
Solo in un caso particolare ho dimostrato che l'espressione tra [] vale 1 cioè nel caso in cui una delle due corde assegnate coincide con il diametro.
scusa Gianluca, ma non ho capito bene come hai fatto a spostare la figura mantenendo le corde uguali a se stesse... e ottenere a=b=c=d ...
per MarcoC: ma alfa e beta non sono uguali...
No infatti, non sono uguali.
Ma nel caso particolare che ho citato, si dimostra che sono supplementari e quindi tutta l'espressione tra [] vale 1.
Purtroppo non sono ancora riuscito a dimostrare che sono supplementari in generale.......
puoi cercare un'altra strada... abbastanza intuitiva...
facendo passare i segmenti per centro cerchio. Una opzione
Caro Gianluca,
ma io voglio delle corde qualsiasi, perpendicolari tra loro...
caro Leandro,
si può ancora compattare di più...
r2 = (a + b)2 + (d- c)2 = ?
Si si , considerando che nel cerchio le corde hanno quest relazione:
si può arrivare a
meno di così non saprei.
Cioè non è r ma il diametro. Si può dire che l area del cerchio avente come raggio il diametro è uguale alla somma delle aree dei cerchi aventi per raggio i segmenti di corde perpendicolari fra loro.
sì, ma... si può compattare di più, facendo comparire anche d... ci stiamo girando attorno... (tra parentesi nella relazione precedente avevo dimenticato di dividere per 2 ... ). Ma il succo è quello e ci si può divertire con le aree come dici tu...
d=sqr[(a+b)^2+(c-d)^2]
Gianluca... ho già pubblicato la risposta...
(a+b)/2cos teta = r
(c+d)/2cos 90-teta = r