Categorie: Matematica Meccanica Celeste
Tags: cerchio costruzione ellisse ellissi quiz
Scritto da: Vincenzo Zappalà
Commenti:10
Costruiamo un'ellisse e imiteremo Newton ***
Ci sono molti modi per costruire graficamente un'ellisse, ma tra i tanti proviamo a trovarne uno che ci permetterà di imitare Newton senza alcuna equazione differenziale. Un quiz che è solo l'ingresso in un mondo straordinario. Chi conosce la storia è pregato di tacere e fare pensare tutti gli altri... grazie!
Qualcuno diceva: "Elementare!" e poi aggiungeva:" Il che vuol dire che è necessario sapere ben poco in anticipo per poterlo capire, ci vuole solo... intelligenza". Vi propongo perciò l'inizio di un percorso molto "elementare", ma non certo banale da seguire nella sua completezza. Vi ricordate quanto è stata complicato da parte di Newton il determinare le leggi di Keplero? Equazioni differenziali a tutto spiano... Bene, se ne può fare anche a meno, ma... si deve rimanere molto elementari e cominciare a risolvere qualche piccolo trucchetto.
Non sono certo io l'artefice di quanto stiamo per iniziare e spero solo di esserne all'altezza... Quando è stato formulato era considerato un "puro divertimento"... speriamo di farlo rimanere tale.
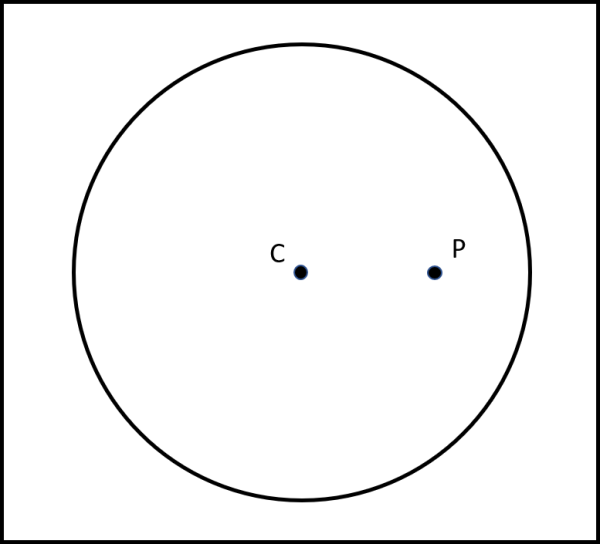
La domanda iniziale, tanto per rompere il ghiaccio, è: "Dato un cerchio di centro C, come si può costruire una perfetta ellisse scegliendo a caso un punto P al suo interno, che sarà poi un suo fuoco?" Ovviamente, non bisogna utilizzare la classica definizione di ellissi come luogo dei punti per i quali la distanza da due punti detti fuochi rimane costante. Questa proprietà servirà a dimostrare che quanto abbiamo costruito è proprio un'ellisse. Una domanda a cui si deve rispondere solo graficamente . Ecco la figura da cui partire:
Il punto P è preso completamente a caso. Cosa tracciare e manipolare per far sì che esso sia uno dei fuochi di una bellissima ellissi costruita graficamente?
Fatto? Bene... Disegnata l'ellisse, dimostriamo, attraverso la sua classica definizione, accennata precedentemente, che essa è proprio un'ellisse!






10 commenti
E' un peccato che nessuno provi a risolvere il quiz. Chi l'ha ideato è un genio infinito e la soluzione è "elementare" nella sua difficoltà...
Poi andremo oltre e sarà bello conoscere ciò che è poco conosciuto... in qualche modo imiteremo Newton...
Scusa Vincenzo ma i due punti della elisse debbono essere coincidenti con la intersezione dell'asse verticale passante per C ed intersecante la circonferenza di raggio R e centro C, ovvero debbono essere coincidenti con la intersezione dell'asse orizzontale passante per C ed intersecante la circonferenza di raggio R e centro C ?
Dunque, data una circonferenza di centro C e un punto P qualsiasi al suo interno, mi iene in mente la costruzione dell'ellisse che ha per fuochi proprio i due punti C e P. Allego il disegno fatto un attimo fa :
Caro Arturo,
i miei complimenti... tu non hai costruito l'ellisse scegliendo un punto che soddisfi la relazione canonica. Hai costruito un punto il quale poi, guarda caso, soddisfa quella relazione. C'è una sottile, ma non ovvia differenza. In realtà sarebbe meglio partire da una qualsiasi linea passante per P e poi fare un qualcosa che individua proprio il punto che hai costruito.
Parliamoci chiaro... stiamo parlando nientemeno che di Feynman!!!
Non è altro che l'introduzione alla lezione perduta di Richard, che si è cercato di rimettere in sesto da vari spezzoni...
caro Michele, il punto P è un punto qualsiasi all'interno della circonferenza. Poi esiste, ovviamente, il centro della circonferenza. Che poi essi risultino i fuochi deriva dalla costruzione che si fa, ma non lo devono essere a priori...
caro Artù, penso che con il tuo geogebra potresti fare un'animazione magnifica...
Teniamo conto che con la costruzione che hai praticamente intuito certe rette risultano tangenti e quindi potrebbero a un certo momento essere utilissime parlando di velocità...
essendo AGC= EGF=PGF essa è un ellisse per la proprietà tangenziale
Caro Vincenzo,
sinceramente la costruzione mi è venuta in mente non come un mio nuovo pensiero personale, ma come se ricordassi di averla già vista in passato da qualche parte. Tieni presente che di Feynman ho letto sinora tre libri e scandagliato , anche se non completamente, il sito web a lui dedicato. Chissà, magari l'avrò vista proprio durante le letture dei suoi libri. Tornerò a sfogliarli per cercarla.
Per fare l'animazione con geogebra, non c'è alcun problema. Se serve posso farla tranquillamente.
Questo è un assaggio
grande assaggio!!! e anche molto... buono!