Categorie: Matematica
Tags: geometria quiz rimbalzi elastici soluzione
Scritto da: Umberto Cibien
Commenti:2
Soluzione del quiz:UNA BIGLIA INTRAPPOLATA
Qui trovate il quiz e i commenti.
Presento la mia soluzione in modo un po' più formale. Questo per dare una spiegazione in più; già leggendo i commenti di Vincenzo (e anche di altri) si riesce a giustificare la soluzione in modo intuitivo-geometrico.Mi baso su una figura, che è un caso semplificato del nostro problema. Nel nostro caso, ricordiamo che n=49,m=78,. Chiaramente questa figura non è quella del quiz, ma serve per chiarire i punti più difficili della soluzione in un caso molto più semplice.
Cominciamo poi col mettere due assi coordinati, con origine in B1; con essi possiamo misurare gli spostamenti (assoluti, in termini di distanza positiva) in x e y della biglia.
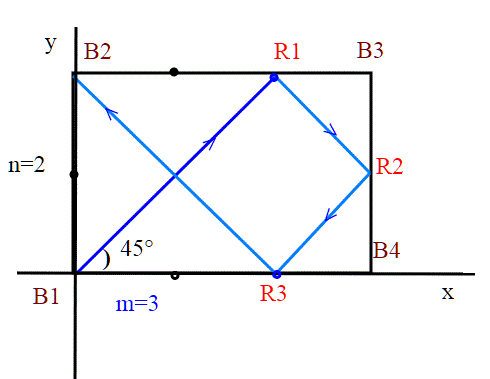
Rifacciamoci alla figura per capire meglio;in questo caso la biglia parte da B1 e finisce in buca in B2. Calcoliamo la somma delle distanze percorse in x e in y:
Sommax=2+1+1+2=6
Sommay =2+1+1+2=6
Questo è un fatto generale del problema;ad ogni rimbalzo a 45° genero due spostamenti x,y sugli assi, e sono uguali. Quindi in un certo punto di arrivo (sponda,buca), la somma degli x sarà uguale alla somma degli y. Indichiamo con Sxi la somma delle xi, Syi la somma delle yi. Si ha che Sxi=Syi. Come già detto, questa è una conseguenza che i rimbalzi siano a 45°.
Ma quand'è che una biglia finisce in una buca?
Quando lo spostamento Sxi è multiplo di m (lato orizzontale del rettangolo 3 x 2) e lo spostamento Syi è multiplo di n. Se entrambi le condizioni sono verificate, dobbiamo proprio trovarci su una buca. Questo si traduce nel fatto che: (detti k1,k2 degli opportuni numeri interi)
Sxi=k1*m, Syi=k2*n. Essendo Sxi=Syi, k1m=k2n. Quindi dobbiamo trovare dei k1,k2 minimi (se finiamo in buca il gioco finisce) per cui sia soddisfatta l'eguaglianza ,k1*m=k2*n. Sono chiaramente k1=n,k2=m. Quindi Sxi=Syi=n*m. Nel nostro esempio: k1*3=k2*2, k1=2,k2=3, Sxi=Syi=3*2=6
Ora analizziamo la formuletta:
Syi=Sxi=m*n guardando il nostro esempio:

quando c'è un rimbalzo su un lato orizzontale, ad esempio siamo in R1, la Syi è diventata multliplo di n (yi è infatti=2). In R1 Syi è 2,in R3 4, in B4 6. Quindi avremo in tutto m rimbalzi sui lati orizzontali,m= m*n/n.. Allo stesso modo, avremmo n rimbalzi verticali. Quindi i rimbalzi totali saranno m+n. I rimbalzi n=2,m=3 vanno in buca, e pertanto non vanno contati come rimbalzi. Quindi m-1+n-1=m+n-2. Nel nostri caso 3+2-2=3 rimbalzi. Nel caso del quiz, m=78, n=49, m+n-2=127-2=125.
Torniamo adesso al nostro esempio base e analizziamo la parità dei rimbalzi in questo senso;
il primo rimbalzo su lato orizzontale è R1 (rimbalzo N°1) ed è a nord;quindi il rimbalzo orizzontale N°2 sarà a sud. Quindi dispari nord, pari sud. Per i verticali R2 (N°=1) dispari a destra e pari a sinistra.

Qui la buca avviene m=3, n=2. I rimbalzi orizzontali sono pari a sud e dispari a nord. Il 3 ° finisce in buca e non rimbalza, e lo fa a nord; il 2° va in buca e non rimbalza, ma essendo pari a sinistra. Quindi la palla va in buca in B2
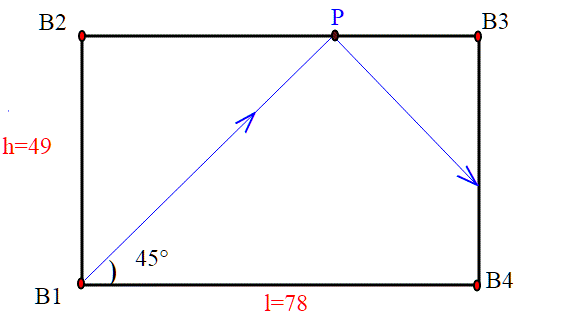
Usiamo un ragionamento analogo sull'esempio base per il nostro quiz;
Qui la buca avviene m=78, n=49, m+n-2=127-2=125. I rimbalzi orizzontali sono sempre pari a sud e dispari a destra. Il 78 ° finisce in buca e non rimbalza, e lo fa a sud; il 49° va in buca e non rimbalza, ma essendo dispari a destra. Quindi la palla va in buca in B4.






2 commenti
scusate il ritardo della soluzione, ma ho avuto gravi problemi di salute che non sono ancora scomparsi del tutto.
ben tornato e ... forza!!!