Questo articolo è stato inserito in "Il moto dei pianeti secondo Feynman", al quale si rimanda per una trattazione completa dell'argomento

 

Il quiz sulla costruzione dell’ellisse era solo un antipasto per una ghiotta e geniale lezione di Richard Feynman. Da Newton a Keplero senza equazioni differenziali e con una matematica e geometria alla portata di tutti coloro che vogliono usare la propria intelligenza e divertirsi, ammirando uno dei più grandi geni al lavoro.

Introduzione

Nel marzo del 1964, Richard Feynman tenne una lezione a dir poco “storica”. L’argomento era quanto di più interessante si potesse desiderare: “Il moto dei pianeti intorno al Sole”. Una lezione che lo stesso Feynman disse ai suoi allievi di aver preparato “soltanto per il piacere di farla e per il vostro divertimento”. Il divertimento per Richard era sempre molto particolare e si riferiva ad argomenti estremamente ELEMENTARI (ossia fondati su basi da liceo), ma non era veramente SEMPLICE, dato che abbisognava di una buona dote di INTELLIGENZA.  La lezione e soprattutto le figure originale sono in gran parte andate perse, ma un suo collega ha ricostruito il contenuto della lezione che può essere seguita da chiunque abbia anche solo un vago ricordo della geometria euclidea. E proprio ciò che faremo noi (o, almeno cercheremo di fare) cercando di semplificare e di estendere ancora di più le parti più “critiche” e fondamentali.

Feynman prende le mosse dall'osservazione di Kepler sul moto dei pianeti intorno al Sole lungo orbite ellittiche e dal fatto che un segmento che congiunge un pianeta al Sole 'spazza' aree uguali in tempi uguali. Rifacendosi a Newton ricorda anche che l'uguaglianza delle aree in tempi uguali è equivalente all'affermazione che la forza varia secondo l'inverso del quadrato della distanza. Ma ciò che emoziona di più è la scoperta che la prima legge di Keplero è una conseguenza delle altre due.

Una volta stabilito che la forza è diretta verso il Sole e che varia secondo l'inverso del quadrato della distanza Newton riuscì a elaborare le combinazioni tra velocità e variazioni di velocità e mostrare che essa era un'ellisse, usando sofisticati e un po’ contorti metodi legati alle molteplici caratteristiche delle “sezioni coniche”. Lo stesso Feynman, con la sua solita ironia, ammette di fare “fatica” a seguirle tutte.  Decide, allora, di elaborare una geniale dimostrazione ELEMENTARE (col particolare significato datogli prima).

Un insieme di raffinati “trucchi” geometrici che superano tutti gli scogli incontrati da Newton nella sua dimostrazione basata sulle sezioni coniche. Insomma… uno dei tanti piccoli-grandi capolavori di Richard.

Il quiz-introduzione pubblicato QUI è solo un antipasto della parte conclusiva con la descrizione della costruzione dell’ellisse, ma penso sia più che sufficiente per destare meraviglia ed emozione.

Spieghiamola con calma e poi lasciamola nel cassetto per riprenderla alla fine, dopo i vari articoli che ci porteranno piano piano fino a lei.

Il colpo di teatro

Consideriamo il nostro cerchio di raggio R, con centro in C. Non ci resta che prendere un punto P qualsiasi all’interno della circonferenza.

Utilizziamo, prima, la versione puramente grafica e di grande effetto. Dal punto P tracciamo un gran numero di segmenti rettilinei (al limite anche infiniti), che vadano a toccare la circonferenza, come mostrato in Fig. 1.

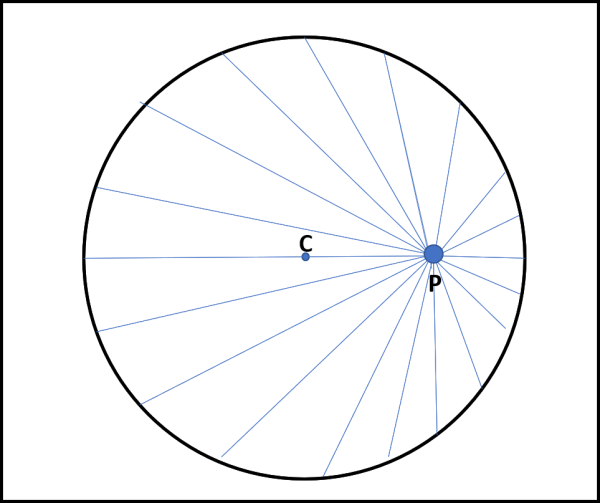
Per ogni segmento fissiamo il punto di mezzo e ruotiamo ciascun segmento di 90° attorno a questo punto, come iniziato a fare in Fig. 2 e, in particolare, per PD.

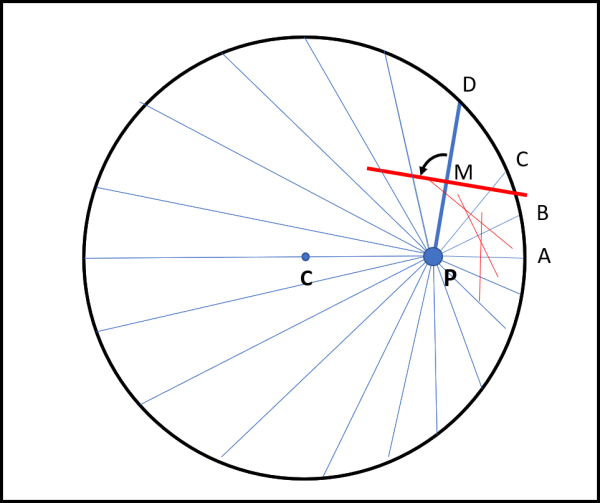
Completata la nostra “manovra”, possiamo tranquillamente eliminare i segmenti iniziali e lasciare solo quelli ruotati di 90°: quello che ci appare è una perfetta ellisse, inviluppo dei segmenti ruotati (Fig. 3).

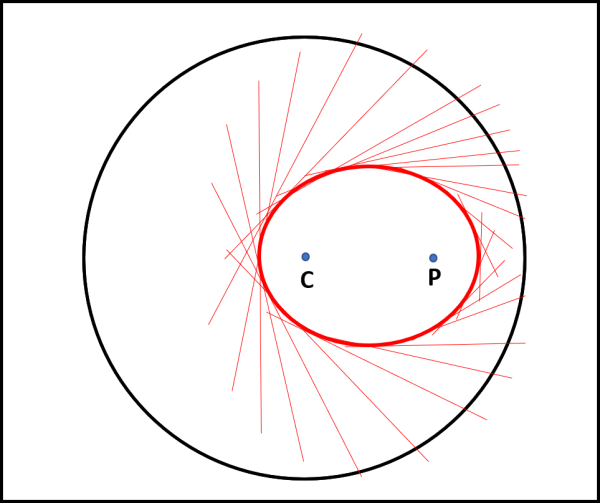
Ovviamente, la messa in scena è ancora più emozionante se i segmenti sono in numero molto grande, come si vede nella fig. 4, in cui è rappresentato l’inizio, un momento intermedio e il finale dello spettacolo.

La costruzione geometrica

“Sì”, mi dirà qualcuno, “la curva è molto bella e assomiglia a un’ellisse con P e C nei due fuochi… ma è proprio un’ellisse? Sarebbe meglio avere una prova definitiva!”. E noi (ossia Feynman) non ha nessuna difficoltà a darla in modo veramente elementare.

Utilizziamo la Fig. 5, dove PA è un qualsiasi segmento originario.

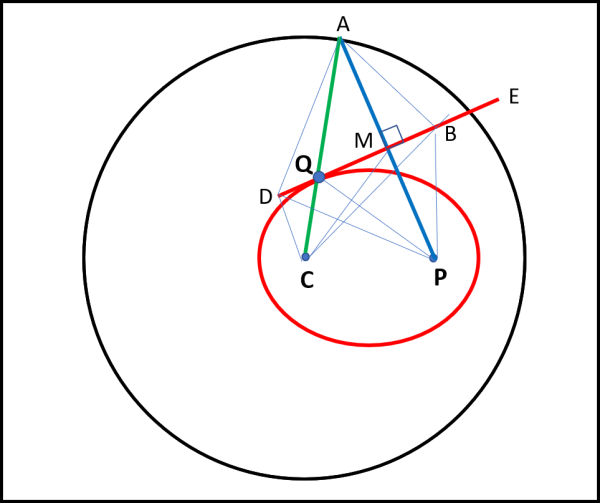
Sia M il suo punto di mezzo e DE il corrispondente segmento ruotato di 90° attorno al punto M. Qualsiasi punto del segmento DE gode di una banale proprietà: esso ha distanza uguale da A e da P. Infatti, ogni triangolo rettangolo del tipo ABM è uguale al suo fratello BMP, avendo il cateto MB in comune e il cateto AM uguale a MP per costruzione. Consideriamo un punto particolare sul segmento DE, ossia quello che sta sul raggio CA. Anche per lui ovviamente vale la relazione:

AQ = QP

Da cui segue che:

CA = CQ + AQ = CQ + QP = R

Il raggio R è ovviamente una costante, per cui la relazione precedente ci dice che la somma delle distanze di Q da C e da P è una costante. Dato che lo stesso procedimento si può fare per qualsiasi segmento iniziale, il punto Q descrive il luogo dei punti che hanno la somma delle distanze da due punti fissi uguale a costante. In altre parole: il punto Q descrive un’ellisse di fuochi P e C.

Fantastico, veramente fantastico.  Per non farci mancare niente utilizziamo l'animazione preparata rapidamente da Arturo (Fig. 6), che mostra l'intera costruzione.

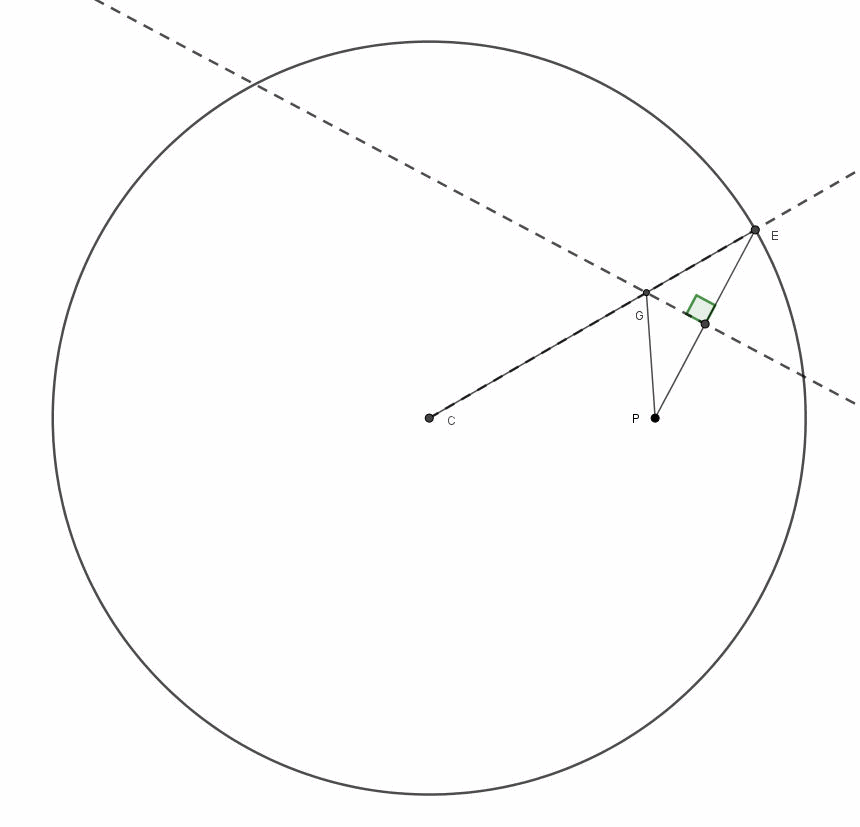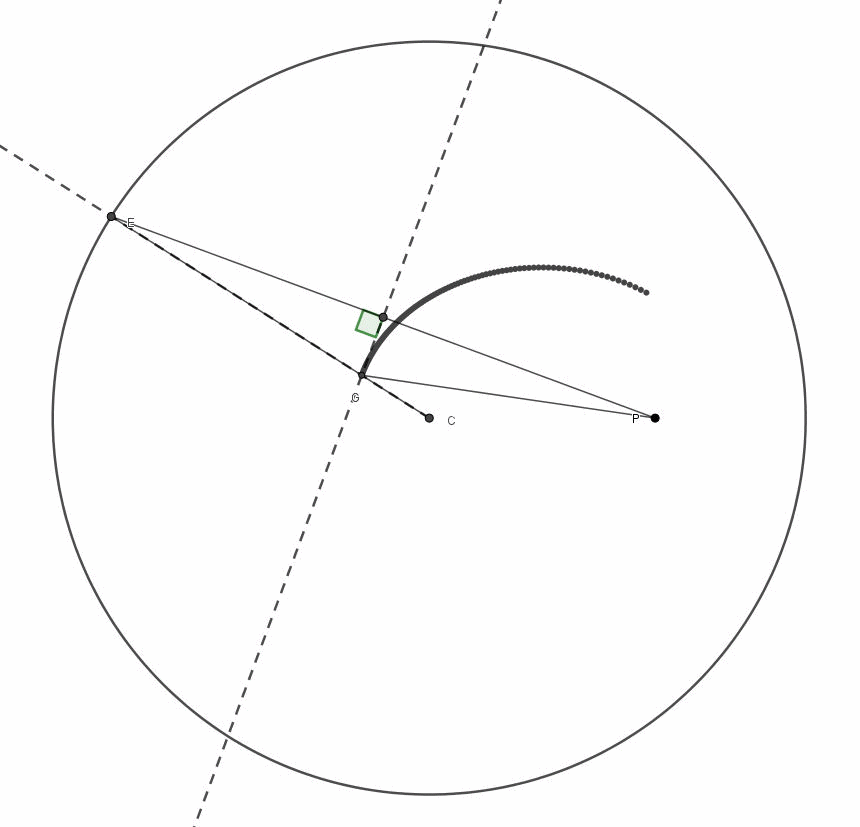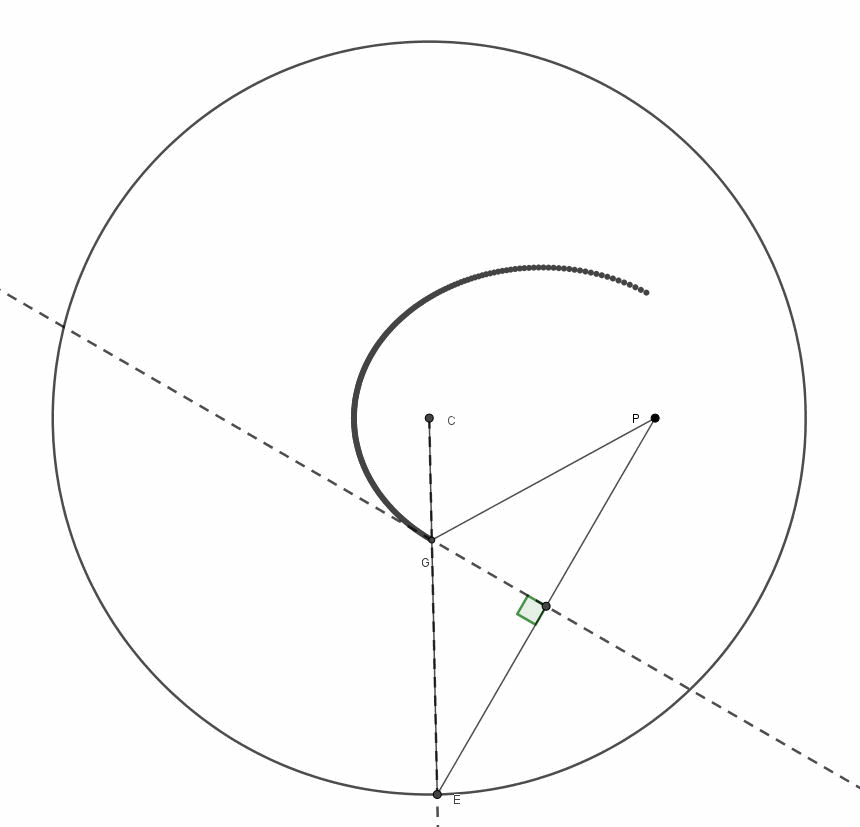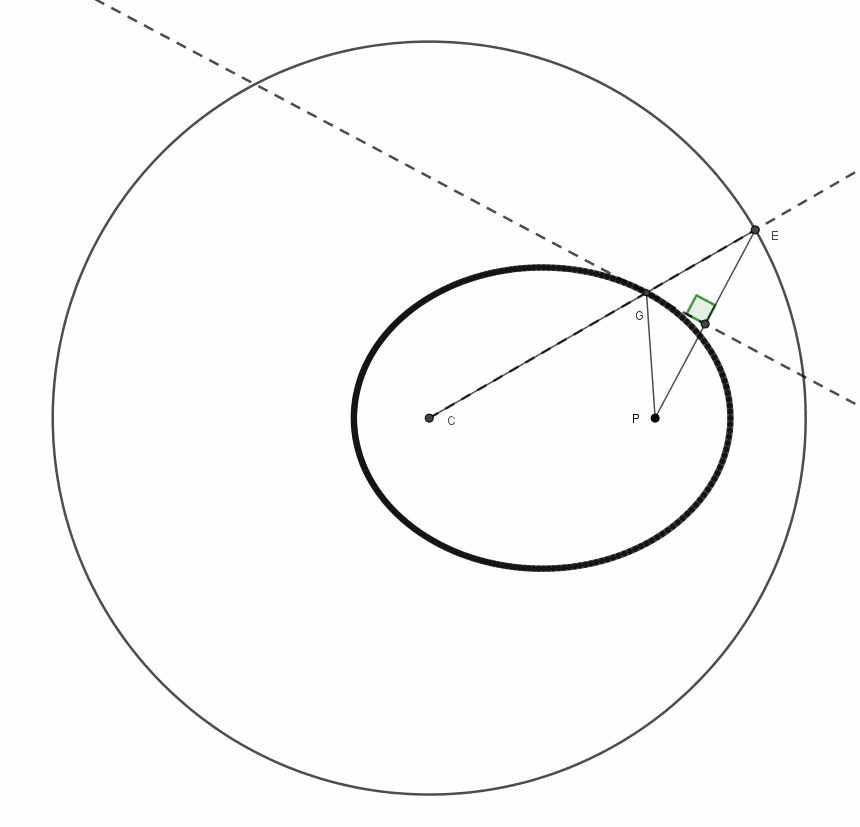
Figura 6

Il fatto più importante, però, è che ogni segmento ruotato di 90° risulta tangente a un punto dell’ellisse e, quindi, indica la direzione della velocità di un corpo che la descrive. Questa banale constatazione sarà utilissima alla fine della nostra “avventura”. Per i più pignoli possiamo facilmente confermare che il segmento ED è tangente alla ellisse nel punto Q, dato che qualsiasi altro punto del segmento (sia a destra che a sinistra di Q) darebbe luogo a una somma maggiore del raggio R del cerchio, ossia:

CD + DA > AC = R

AM + MC > AC = R

AB + BC > AC = R

Continua... e non perdetevi il seguito!