Categorie: Fisica classica
Tags: dromedari gemelli Eratostene quiz treno
Scritto da: Vincenzo Zappalà
Commenti:20
Quiz: Eratostene e due dromedari **
Sappiamo molto bene che Eratostene per mezzo di un bastone e di un dromedario dal passo perfettamente cadenzato era riuscito a misurare la circonferenza della Terra con una precisione fantastica. Immaginiamo di trasportarlo ai giorni nostri e di prospettargli un quiz...
Dopo avergli spiegato brevemente cos'è un treno e averlo portato in una stazione ferroviaria, gli poniamo il seguente problema: "Ti permettiamo di utilizzare il tuo dromedario, ma nessun altro mezzo. Sapresti calcolare la lunghezza di un treno qualsiasi, che passi a velocità costante nella stazione senza fermarsi, in termini di passi del tuo dromedario? Tieni conto che il treno potrebbe arrivare sia da destra che da sinistra...".
Eratostene ci pensa un attimo e poi chiede soltanto di avere con sé anche il fratello gemello del suo dromedario, che cammina con la sua stessa cadenza perfetta. A questo punto chiede per favore che vi siano due persone che guidino i dromedari ovunque vadano e stiano attenti ai passi che compiono, senza alcun bisogno di comunicare tra di loro e con lui.
Non ha bisogno di nient'altro, né bastone, né clessidra. Lo si sente mormorare: "Ho misurato la Terra, figuriamoci se non riesco a misurare un treno o come si chiama quel mucchio di ferro che corre come un matto...!". Non gli resta che aspettare il primo treno di passaggio e poi, disegnando soltanto su un papiro, riesce a dare la risposta!
Come ha fatto?
Ovviamente, per rispondere, dovete fare lo stesso disegno di Eratostene...
La soluzione la trovate QUI






20 commenti
Scusa Vincenzo ma Eratostene immaginario deve necessariamente utilizzare tutti e due i dromedari ?
se riesci con uno solo, vuol dire che mi sono sbagliato... cose che capitano.
I 2 cammelli devono essere posti ad un distanza maggiore della lunghezza del treno.
Sia c1 il cammello più vicino alla testa del treno e c2 il cammello più distante.
C2 parte subito in direzione di c1 mentre c1 aspetta.
Quando la coda del treno passa c1, allora si muove in direzione di c2.
Quando c2 incontra la testa del treno eratostene scrive il numero di passi nel suo taccuino (di papiro?) Diciamo P1.
C1 prosegue e c2 pure. Quando si incontrano, eratostene segna di nuovo i passi di c2, diciamo P2.
La lunghezza del treno e' 2 P2 - P1.
Caro Leandro,
la frase : ad un distanza maggiore della lunghezza del treno" non mi piace dato che implica una conoscenza pur vaga della lunghezza del treno. Tuttavia, la strada è giusta, ma si può fare anche di meglio e senza alcuna idea della lunghezza del treno...
Inoltre, Leandro, non si capisce bene dove metti C1 e C2 e quando parte C2... Sei troppo ermetico.
Teniamo anche conto che (l'ho aggiunto nel testo) che Diomede non può sapere da che parte arriva il primo treno
Forza "quizzari"! Vi spaventate per due dromedari pacifici????
Ci vogliono due dromedari per eliminare la misura temporale. Si fa minkosky e da qui si identificato due triangoli simili. É sufficiente fare il triangolo dei dromedari che si avvicinano e misurare i passi che fanno quando incrociano sia la testa che la coda del treno. Il disegno é più facile se il treno è più veloce dei dromedari ... ovviamente.
caro Leando,
sei veramente ermetico nelle tue risposte... cosa vuole dire:
"É sufficiente fare il triangolo dei dromedari che si avvicinano" ?
e, inoltre:
"misurare i passi che fanno quando incrociano sia la testa che la coda del treno" ?
Partendo da dove e andando dove?
E ... scusa, che c'entra Minkowski? Le velocità sono quelle dei treni normali...
Dai, se non vuoi o puoi fare un disegno, cerca di essere più preciso e comprensibile...
Non pensavo mai più che il vecchio Eratostene fosse molto più bravo dei nostri quizzari, O forse sono stufi di quiz? Basta dirmelo e smetto...
Allora, prendiamo i due cammelli e li mettiamo fermi di schiena.
Appena la testa del treno transita nel punto dei due cammelli, essi partono e contano i passi fino quando raggiungono la coda del treno o sono raggiunti dalla coda.
A questo punto chiamiamo C1 il cammello che si vede arrivare in faccia il treno (cioè quello che si muove nel verso contrario del treno) e C2 il cammello che invece si muove nella direzione del treno. I rispettivi passi contati saranno P1 e P2.
Ora tracciamo le curve di moto dei cammelli C1 e C2, della testa del treno (T) e della coda del treno (C) in un grafico cartesiano (Eratostene lo chiamava in modo diverso, ma non aveva problemi a tracciarlo) con lo spazio S in ascisse ed il tempo di percorrenza t in ordinate. (Non riesco a riportare i grafici, quindi proverò a spiegare a parole il processo, anche se in via grafica è più chiaro).
L'origine la scegliamo nel punto di partenza dei due cammelli (S=0) al momento in cui la testa T arriva (t=0).
Essendo tutti a velocità costante (vC i cammelli e vT il treno), i diagrammi di moto saranno semirette:
C1, con partenza nell'origine degli assi, sarà una semiretta nel quadrante S<0,t>0, inclinata di un angolo α rispetto all'asse delle ordinate.
C2 sarà la semiretta simmetrica a C1 (nel quadrante S>0, t>0) ed inclinata sempre di un angolo α
T sarà una semiretta con partenza nell'origine degli assi, ed inclinata di un angolo β rispetto all'asse delle ordinate. Ipotizziamo che vT sia maggiore di vC (ipotesi ragionevole, perché se il cammello non corre è un animale placido)
C sarà una semiretta parallela a T con partenza al tempo 0 nel punto di ascissa negativo pari alla lunghezza del treno (LT).
L'intersezione della retta C1 con la retta C (cammello 1 con la coda del treno) avviene nel quadrante S<0 a P1 passi dall'origine (noti), ad un tempo t1 (ignoto, ma privo di rilevanza).
Analogamente l'intersezione della retta C2 con la retta C (cammello 2 con la coda del treno) avviene nel quadrante S>0 a P2 passi dall'origine (noti), ad un tempo t2 (ignoto, ma privo di rilevanza).
Sia dal disegno, sia dalla composizione delle velocità vC e vT si vede che P2>P1.
Se tracciamo le rette parallele all'asse delle ascisse passanti per t1 e t2, esse intersecano la semiretta T nei punti di ascisse T1 e T2 che rappresentano la posizione della testa del treno al momento in cui la coda interseca C1 e C2 rispettivamente.
Tracciamo anche la semiretta parallela a C1 passante per il punto T1,t1. Tale semiretta interseca l'asse delle ascisse in un punto pari a LT
Ora con un po' di geometria (che Eratostene conosceva molto bene) vediamo che:
P1:P2=t1:t2
Osserviamo che t1=T1/vT e t2=T2/vT. Perciò sostituendo nella proporzione precedente ed eliminando vT, abbiamo:
P1:P2=T1:T2
Ora si nota anche che:
LT=T1+P1
ma anche:
LT=T2-P2
Sostituendo nelle proporzioni e maneggiandole un po', risulta che la lunghezza del treno è (in bianco)
LT=2*P1*P2/(P2-P1) se non ho commesso errori.
Alcune osservazioni:
Le ipotesi di lavoro sono:
Ora circa la scelta del sistema di coordinate: l'importante è che i cammelli devono camminare in verso opposto tra loro e nella stessa direzione del treno, e che contino i passi P1 e P2 dal momento in cui sono con la testa del treno fino al momento in cui sono con la coda. Poi possono incontrarsi in qualsiasi momento, prima dell'arrivo del treno o anche dopo, in stazione o in aperta campagna, ma non è importante.
Infatti possiamo prendere il sistema di riferimento della posizione dei cammelli ovunque, ed in qualsiasi tempo, ma se è fermo (come è fermo quello della stazione di transito dei treni), posso disegnare il sistema di riferimento ed i cammelli su un foglio di carta lucida e segnare lì i punti di intersezione con il treno. Poi il foglio lucido lo traslo su quello della stazione e riottengo il grafico descritto.
Mi sono mangiato una frase: l'ipotesi che vT>vC, vuol dire che α<β e quindi C interseca anche C2.
Scusate
Caro Francesco... volendo un risultato soltanto grafico, direi che questa parte è inutile:
"Osserviamo che t1=T1/vT e t2=T2/vT. Perciò sostituendo nella proporzione precedente ed eliminando vT, abbiamo:
P1:P2=T1:T2
Ora si nota anche che:
LT=T1+P1
ma anche:
LT=T2-P2
Sostituendo nelle proporzioni e maneggiandole un po',.... "
è inutile. Basta un segmento...
A e B sono i due cammelli posti ad una certa distanza 'c' uno dall'altro.
Sia l la lunghezza del treno.
Partono nella stessa direzione del treno quando questo incrocia B.
B si ferma quando incrocia la coda del treno, sia questo il segmento b.
A si ferma quando incrocia la testa del treno, sia questo il segmento a.
l sta ad b come (c+a) sta ad a

l= (c+a)b/a
seconda soluzione (peccato che non si possa inserire l'immagine):
A e B sono i due cammelli posti ad una certa distanza uno dall'altro.
Sia l la lunghezza del treno.
A parte verso B quando il treno incrocia B fino a quando A non incrocia la testa del treno: segmento a.
Prosegue poi fino ad incrociare B: segmento c
B parte quando incrocia la coda del treno fino ad incontrare A: segmento b
l sta alla differenza dei percorsi dei 2 cammelli a+c-b come c+b sta ad a

l= (a+c-b)(b+c)/a
In realtà si possono inserire i disegni... ma io in quelle cose non sono esperto. Lo abbiamo già spiegato varie volte, ma non so dove recuperare i commenti relativi. Non potresti fare un disegno, farne la scansione e poi inserirlo come immagine?
Comunque, Elio... terrò conto dei tuoi suggerimenti nella soluzione... (i disegni li posso fare sempre io... ).
).
Caro Elio,
non ho avuto tempo stamattina... e oggi e domani sono ultra impegnato con amici. Perché non fai i due disegni e me li mandi privatamente? Penserò poi io a metterli in visione. Ricorda che non ho bisogno di calcoli tra triangoli simili, ma solo della soluzione grafica.
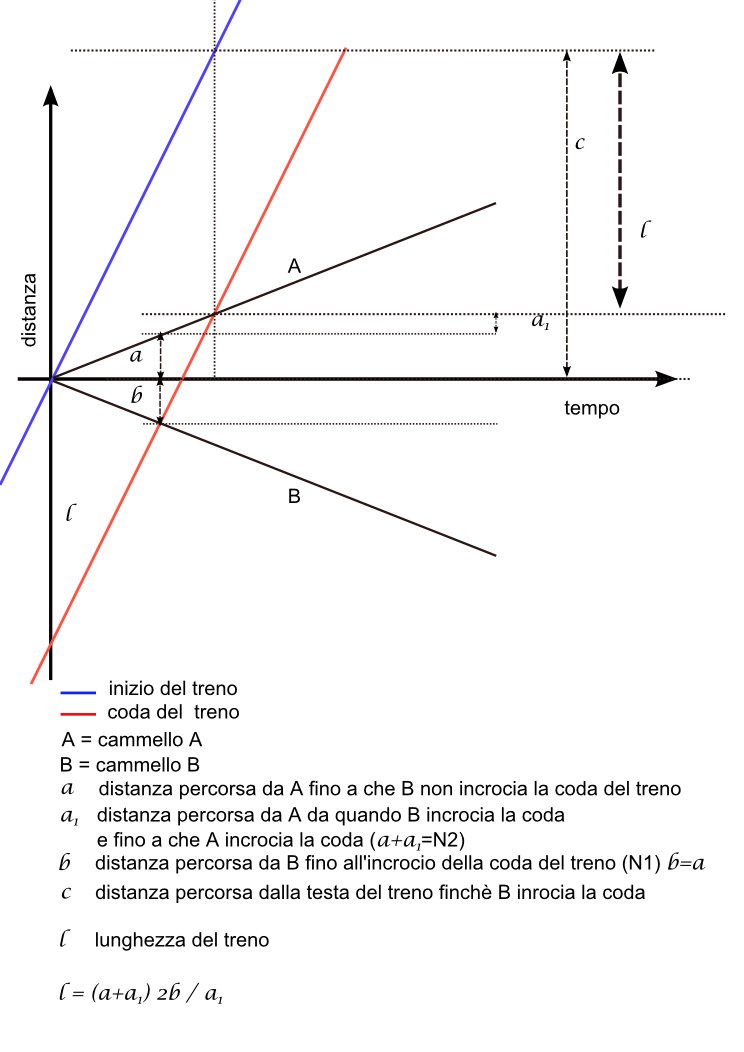
I 2 cammelli sono insieme nel punto O e partono uno nella direzione del treno e uno in direzione contraria nel momento che la cima del treno passa loro davanti. Il cammello che viaggia in senso opposto al treno incontrerà per primo la fine del treno stesso e a questo punto si ferma. Quando la fine del treno raggiunge il secondo cammello anche questo si ferma.
Il primo cammello ha percorso N1 passi e il secondo N2 passi
Mentre la coda del treno percorre la distanza in passi tra i 2 cammelli (N2+N1) il secondo cammello percorre un numero di passi N2-N1. Il treno percorre (a parità di tempo) un percorso (N2+N1)/(N2-N1) volte più lungo rispetto al cammello. Quando la coda del treno raggiunge il secondo cammello (cioè si trova a N2 passi dall'origine), la cima ha percorso (e quindi è spostata rispetto all'origine O) di N2 * (N2+N1)/(N2-N1) passi.
Il treno è pertanto lungo N2 * (N2+N1)/(N2-N1) - N2 passi di cammello
Con un esempio è più chiaro:
Supponiamo che quando i cammelli partono facciano 20 passi prima che la fine del treno incontri il primo cammello, che a questo punto si ferma. Il secondo cammello fa ancora 5 passi e poi viene raggiunto dalla fine del treno.
La fine del treno ha percorso un tragitto di 45 passi mentre il secondo cammello ne percorreva 5. Cioè il treno è 9 volte più veloce del cammello. Il secondo cammello ha percorso 25 passi, quindi la cima del treno sarà 9x25 passi più avanti e visto che il cammello è a 25 passi dalla partenza, il treno è lungo 200 passi di cammello
Interessante la soluzione di Mario.
Professore come faccio a mandarle privatamente i grafici?
Rivedendo nel weekend quello che ho postato mi rendo conto di essere stato approssimativo nell'esporre il ragionamento fatto e nel formulare grafici ed equazioni. Ho quindi sistemato i grafici e l'equazione.
soluzione 1
A e B sono i due cammelli posti ad una certa distanza 'c' uno dall'altro.
Sia l la lunghezza del treno.
Partono nella stessa direzione del treno quando questo incrocia B.
B si ferma quando incrocia la coda del treno, sia questo il segmento b.
A si ferma quando incrocia la testa del treno, sia questo il segmento a.
l sta ad b come c sta ad a
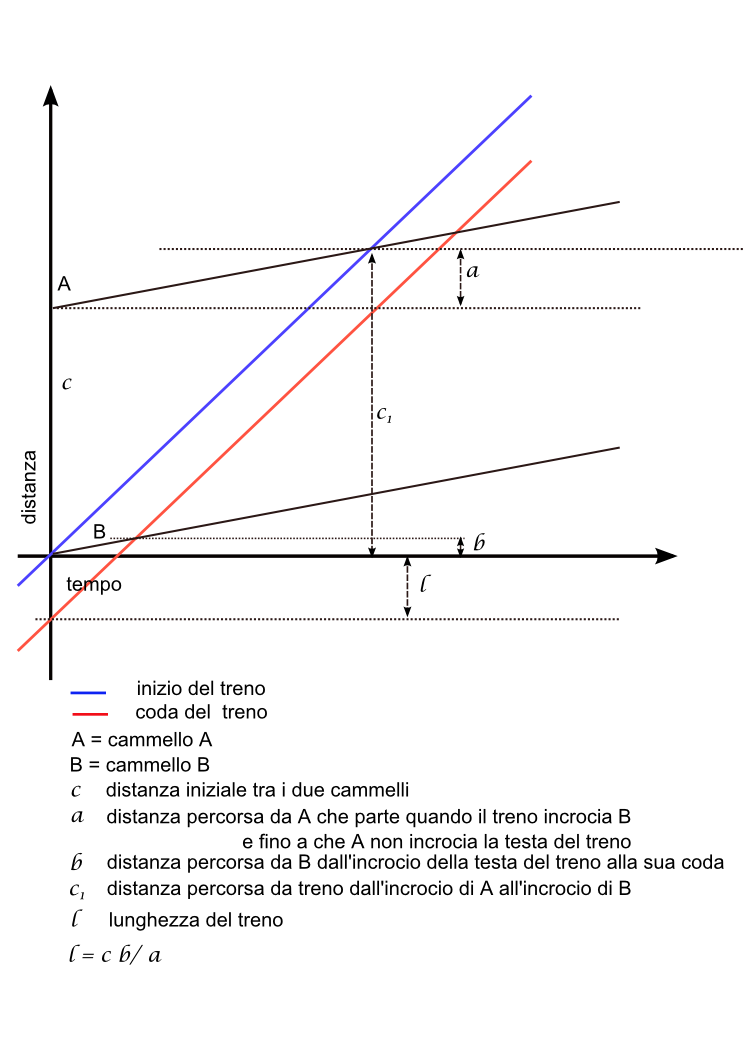
l = c b /a
Ho semplificato, per chiarezza si potrebbe dire che:
l+b sta a b come c+a sta ad a
Allo stesso modo si potrebbe semplificare la soluzione di Mario -che trovo molto elegante- così:
l = 2(N1)(N2) / (N2-N1)
l = 2b(a+a1) / a (nel mio grafico)
soluzione 2
A e B sono i due cammelli posti ad una certa distanza 'c' uno dall'altro.
Sia l la lunghezza del treno.
A parte verso B quando il treno incrocia B; fino a quando A non incrocia la testa del treno: segmento a. (c1 = c-a)
Prosegue poi fino ad incrociare B: segmento a1
B parte quando incrocia la coda del treno fino ad incontrare A: segmento b
l sta alla differenza dei percorsi dei 2 cammelli a+a1-b come c1 sta ad a
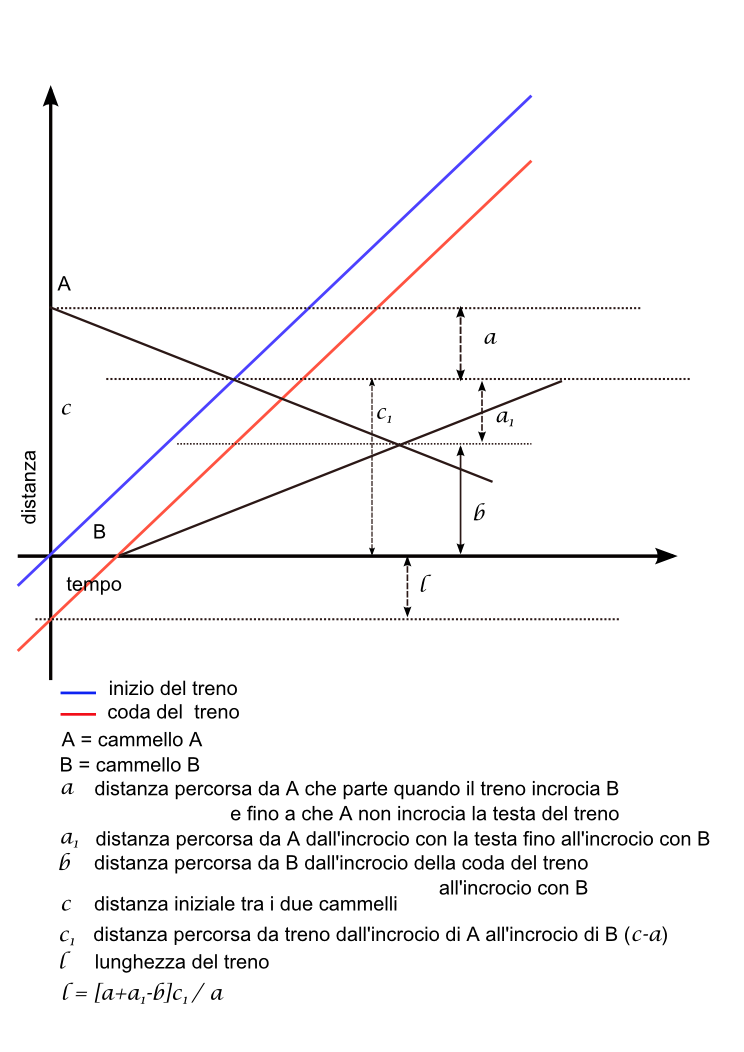
l= (a+a1-b) c1 / a