Un semplice esercizio basato solo sulla conoscenza dello spazio percorso, del tutto indipendente dalle velocità in gioco e, quindi, anche dal tempo che si impiega a fare le necessarie operazioni. Evviva i dromedari!

Francesco e Mario hanno raggiunto lo scopo così come Leo, anche se utilizzando strategie diverse. Io spiegherò la più semplice, basata solo e soltanto su una determinazione grafica.

Eratostene non ha orologi e quindi non può misurare alcun tempo. Ne segue che una determinazione diretta della lunghezza del treno è del tutto impossibile. Teoricamente, non conosce nemmeno la velocità dei propri dromedari, ma ne ha due a disposizione che sicuramente viaggiano alla stessa velocità, anche se questa è una grandezza del tutto sconosciuta. L'uguaglianza delle due velocità rende il problema risolvibile attraverso soltanto misure di distanze, espresse in passi dromedariani (si dice così?). Eratostene decide di mettere i due dromedari "sedere" contro "sedere" e aspettare il treno che potrebbe arrivare sia da destra che da sinistra. La Fig. 1 illustra la situazione di partenza e le azioni da svolgere.

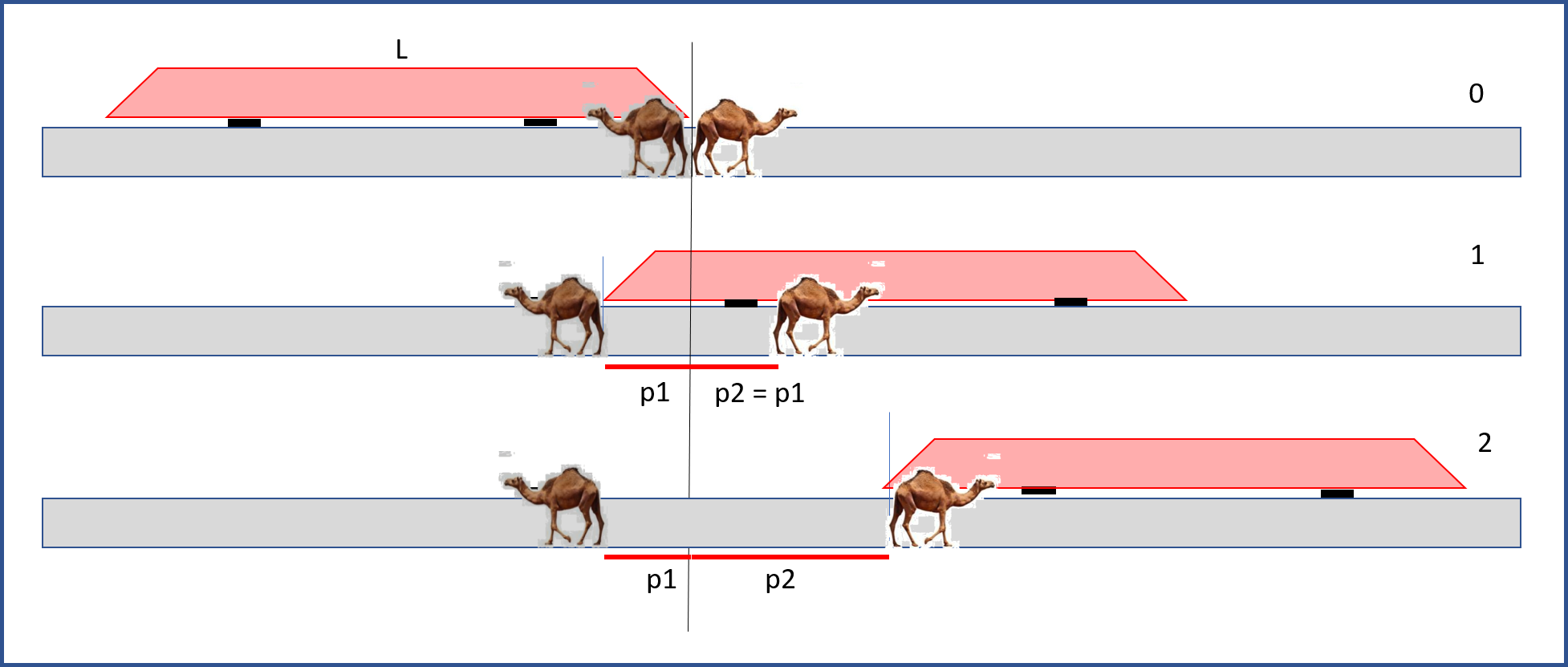
Nel momento in cui la testa del treno giunge esattamente nella linea di divisione tra i due "sederi" dromedariani, li fa muovere col loro passo perfettamente cadenzato. Immaginiamo che il treno di lunghezza L arrivi  da sinistra. Il dromedario D1 va in verso contrario al treno e si ferma esattamente quando la coda del treno arriva alla sua altezza. In questo periodo di tempo (del tutto ininfluente) i suoi passi sono stati p1. Il dromedario di destra D2 si muove invece nello stesso verso del treno. Nel momento in cui si ferma il dromedario D1,  i passi di D2 sono anche loro p1 (vanno alla stessa velocità). Tuttavia D2 continua a camminare fino a che non lo raggiunge la coda del treno. In quel momento, posteriore alla fermata di D1, i passi compiuti da D2 sono p2.

Abbiamo a nostra disposizione solo i valori di p1 e di p2.

Non ci resta, allora, che disegnare un semplice sistema di coordinate spaziotemporali. In ascissa mettiamo lo spazio percorso (ossia il numero di passi) e in ordinata il tempo trascorso. Non ci interessa assolutamente sapere quanto tempo sia passato prima della fermata di D1, né quanto ne sia passato prima della fermata di D2. Sapendo che i due dromedari hanno la stessa velocità (incognita, ma poco ci importa), possiamo disegnare il tratto p1 a un qualsiasi tempo T1, mentre il tempo in cui disegnare p2 sarà legato alla velocità imposta a caso per D1. Basta, perciò, tracciare una traiettoria che formi lo stesso angolo in verso (spaziale) contrario a quello di D1 e fermarla al tempo T2, quando la sua ascissa sarà uguale a p2, come vediamo in Fig. 2a, dove l'origine O è posta nel punto in cui i dromedari sono ancora fermi e vengono raggiunti dalla testa del treno.

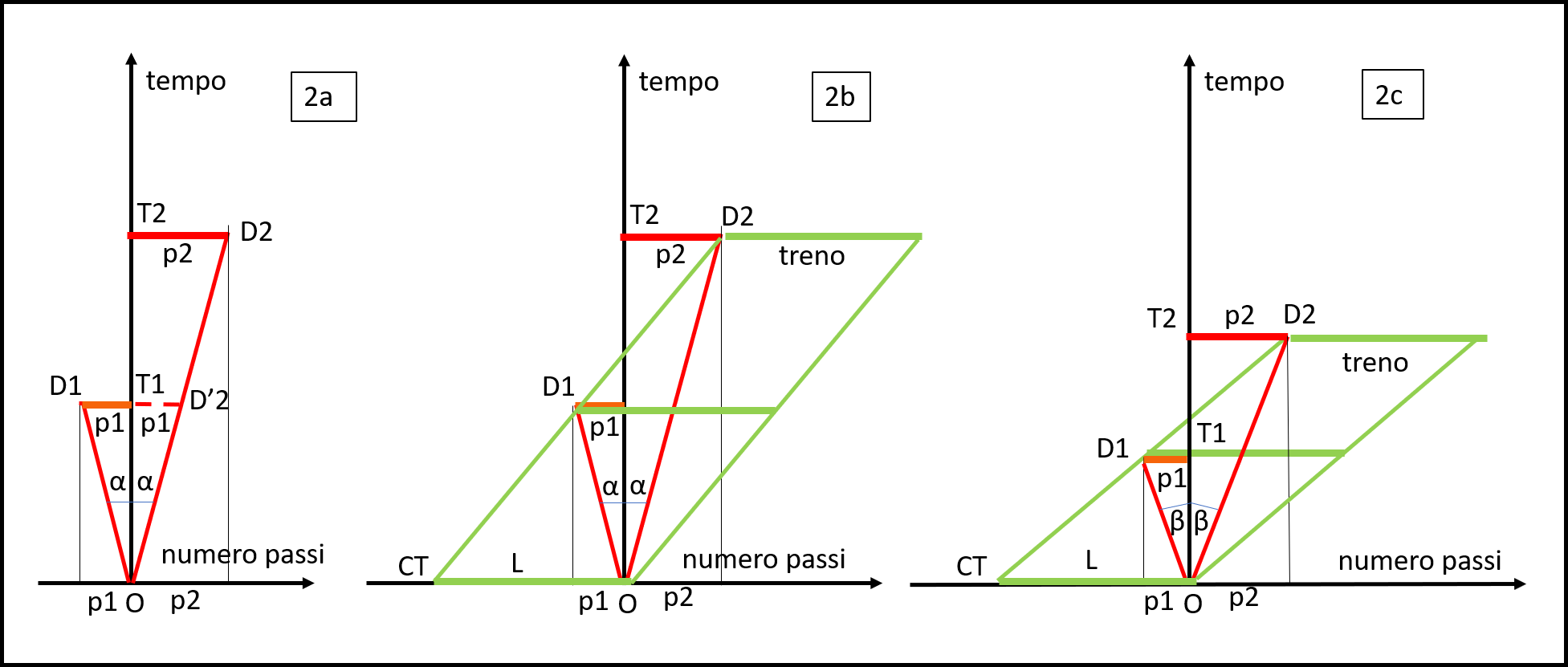
Dove è la testa del treno al tempo zero? Ovviamente in O, ma non sappiamo la sua lunghezza e, quindi, nemmeno dove sia la sua coda. Tuttavia, sappiamo sicuramente che la coda del treno deve passare per D1 e per D2. Basta, perciò, tracciare la retta D2D1 fino a incontrare l'asse x. La distanza in passi tra O e CT è proprio la lunghezza del treno L. L'informazione fondamentale è la pari velocità dei dromedari: solo così riusciamo a sapere dove tracciare il segmento T2D2 pari a p2. La Fig. 2b mostra il nostro treno (in verde) sia nel momento in cui la sua testa è in O, sia in quello in cui la coda raggiunge D1, sia in quello in cui la coda raggiunge D2.

La Fig. 2c ci mostra come sia stata del tutto ininfluente la scelta del tempo T1 in cui tracciare p1. L'importante è che D2 si muova nello stesso modo di D1 in senso opposto e permetta di trovare il valore T2, dove tracciare p2. Cambiano, ovviamente, tutte le velocità in gioco, ma la lunghezza del treno risulta sempre la stessa.

Se il treno fosse arrivato dall'altra parte, le figure avrebbero ruotato di 180° attorno all'asse del tempo, mantenendo lo stesso risultato (a parità di lunghezza del treno).

Ovviamente, il risultato si può interpretare attraverso triangoli simili e cose del genere... ma ad Eratostene bastava fare una figura sul papiro per determinare la lunghezza del treno misurata in passi dromedariani!

Il Quiz lo trovate QUI