LA SFERA DI POINCARÉ 3). Le trivarietà.
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Gli altri articoli di questa serie (LA SFERA DI POINCARÉ) , li trovate nel'archivio--> Matematica e geometria-->Matematiche pure
Come specificato nel riassunto, , scopo di tale articolo è spiegare in modo un po' più semplice il concetto di spazio "curvo" ovvero di varietà tridimensionale, abbreviata in tri-varietà.
Premessa
Le trivarietà sono varietà topologiche di dimensione 3. I primi contributi sostanziali alla teoria topologica delle trivarietà furono portati a cavallo del 1900 da Henri Poincaré, Max Dehn e Poul Heegaard. Una difficoltà nello studio delle trivarietà è dovuta al fatto che la visualizzazione diretta deve parzialmente cedere il posto a rappresentazioni astratte. Molte superfici possono essere visualizzate perché si possono vedere esternamente dalla terza dimensione , una dimensione più alta della dimensione della superficie. La dimensione in più consente alla superficie di piegarsi e chiudersi su se stessa. Si potrebbe tentare di visualizzare esternamente una trivarietà, come se la si vedesse da uno spazio a quattro o più dimensioni, ma acrobazie simili, in effetti, non sono necessarie.
Le possibili "forme" del'universo.
Migliaia di anni fa molti pensavano che la Terra fosse piatta. La piattezza della superficie terrestre doveva essere sembrata evidente a chiunque avesse spaziato con lo sguardo sul mare o o su una pianura; da ciò si concludeva, e non del tutto senza ragione, che la superficie della Terra dovesse essere o infinita o avere un bordo.

Oggi sappiamo,che questo è errato: ciò di cui ci si rende conto meno spesso è che le medesime osservazioni locali potrebbero essere determinate da un numero illimitato di forme terrestri.
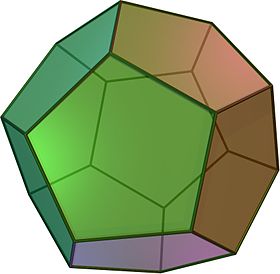
Potrebbe anche essere che la terra avesse una forma irregolare o a «salvagente» (toro).Pensando invece alo spazio, un osservatore sulla Terra non può concludere che l'universo conservi la struttura geometrica dell'ordinario spazio euclideo a distanze indefinite, sebbene non vi sia ancora nessuna prova del contrario. Se la struttura dell'universo non è euclidea, quali sono le alternative?

<<Un'idea è che lo spazio possa essere «curvo», così come può essere curva una superficie. La curvatura tridimensionale dello spazio e la curvatura quadridimensionale dello spazio e del tempo (un concetto strettamente legato al precedente) sono diventate idee importanti in astronomia e in cosmologia a causa del loro ruolo chiave nella teoria della relatività generale di Einstein. Alcuni tipi di strutture tridimensionali possibili dell'universo si possono specificare per analogia con le superfici bidimensionali. In realtà, poiché lo spazio e il tempo sono trattati nella teoria della relatività come una singola entità chiamata spazio-tempo, si potrebbe supporre che la struttura matematica appropriata dell'universo debba essere quadridimensionale. >>
Ma,come continua William P. Thurston:
<< Vi sono buone ragioni per credere, comunque, che la struttura quadridimensionale dello spazio-tempo sia governata dalla struttura tridimensionale dello spazio solo. Pertanto, per studiare la struttura complessiva dell'universo senza pregiudizi, bisogna prima comprendere i tipi di strutture tridimensionali che possono dare origine all'universo osservato. Le strutture vengono chiamate varietà tridimensionali o, per abbreviare, trivarietà. >>
Noi ci occuperemo, come Riemann inventore del termine varietà, solo di varietà matematiche, e per quanto riguarda la "forma" dell'universo, di varietà tridimensionali.

(per chi vuole approfondire dal punto di vista pratico la costruzione di una di una figura come il nastro di Mobius consiglio questo articolo di Maurizio)
Lo studio delle trivarietà è, in un certo senso, una generalizzazione dello studio delle varietà bidimensionali, cioè delle superfici. I topologi hanno scoperto come descrivere e classificare tutte le possibili bivarietà da oltre un secolo, ma la classificazione sistematica di tutte le trivarietà rimane un problema irrisolto, per le forme estremamente complesse a cui danno luogo talune trivarietà.
Le varietà topologiche.
Vogliamo approfondire un po' il concetto di varietà topologica. Le abbiamo già introdotte in questo articolo .Sempre nello stesso articolo abbiamo introdotto il concetto di spazio localmente euclideo, che serve proprio per la definizione di varietà. Rimando sempre all'articolo citato sopra per una definizione più accurata. Qui parleremo solo di una definizione semi-intuitiva tramite una figura e una piccola definizione:
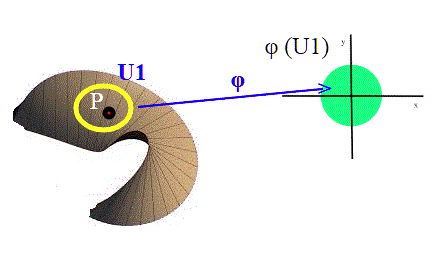
Facciamo risaltare il discorso del localmente euclideo; la varietà del disegno può non essere omeomorfa a tutto il piano euclideo. In caso contrario si parlerebbe di "globalmente", e non "localmente". Tuttavia, per ogni punto della varietà, riusciamo a trovare un intorno sufficientemente piccolo,omeomorfo ad un disco del piano euclideo. Questo significa "localmente euclideo".
Le trivarietà altro non sono che varietà topologiche di dimensione 3, mentre sappiamo che le superfici sono varietà topologiche di dimensione 2. Concettualmente, le trivarietà sono una estensione delle superfici bidimensionali. Come detto in precedenza,i matematici scoprirono che è possibile rappresentare le superfici bidimensionali in modo astratto, usando dei poligoni. Noi lo abbiamo visto varie volte, ma concentriamo ora la nostra attenzione su come si costruisce un toro, che potete vedere in dettaglio qui.
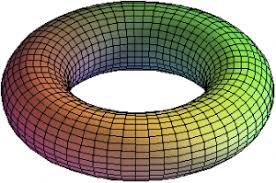
partiamo da una striscia quadrata ,
Lo schema della costruzione è questo:
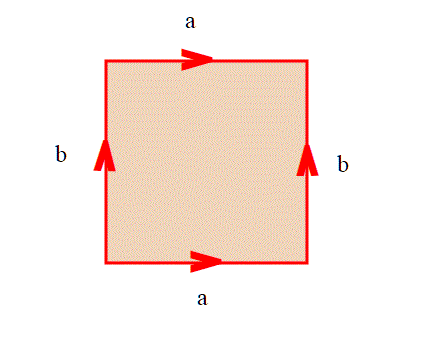
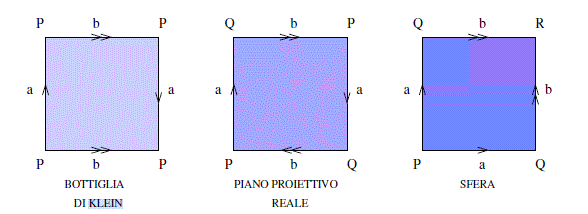
Senza entrare nei dettagli tecnici (insiemi quoziente ed altro, che potete vedere nell'articolo citato) si tratta adesso di identificare i due lati mantenendo i versi delle frecce, cioè incollarli.Dapprima incolliamo i due lati a, nello stesso verso, poi i due lati b, sempre nello stesso verso. Con la prima operazione otteniamo un cilindro, con due bordi circolari; se piegandolo incolliamo i due bordi (pensate a un tubo di gomma), otteniamo proprio il nostro salvagente (Toro).
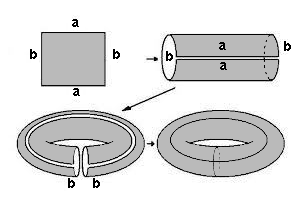
Il toro come possibile mondo bidimensionale
Facciamo una piccola parentesi, e pensiamo a questo toro costruito astrattamente come ad un possibile mondo bidimensionale che non sia ,come nella nostra realtà, la superficie di una sfera.
Nel romanzo Flatlandia, di Edwin A. Abbott, si descrive una creatura bidimensionale che vive interamente nel piano. Consideriamo i movimenti di una tale creatura su una bivarietà con la topologia di un toro, cioè un quadrato i cui lati opposti coincidano con un verso opportuno. Vogliamo vedere come si muove tale creatura in un tale mondo (varietà topologica) bidimensionale.
Per semplicità grafiche associamo la nostra creatura ad un righello, che chiameremo R.
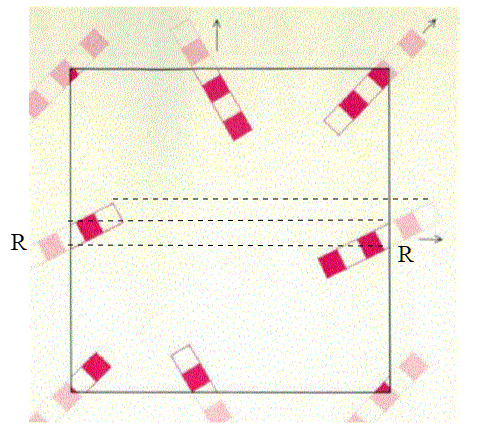
se R esce da destra, rientra da sinistra;se esce dall'alto rientra dal basso. Il salvagente e il quadrato con il lati identificati sono considerati dal punto di vista topologico come la stessa varietà , cioè il toro. Il toro è una superficie localmente euclidea.
Proseguiamo con le nostre costruzioni astratte, ma questa volta nel tridimensionale.

Immaginiamo di avere un cubo nello spazio usuale tridimensionale; possiamo semplicemente pensare ad una stanza . Per analogia per quanto visto sopra, incolliamo in senso astratto il pavimento (2) con il soffitto (1); la parete di fronte (5) con la parete posteriore (6); la parete sinistra (3) con la parete destra (4).Se le incollature venissero fatte davvero, si dovrebbe immaginare la stanza che si piega e si salda con se stessa in una quarta dimensione. Tutto ciò che è necessario per la descrizione della varietà, comunque, è dato dalla procedura delle incollature astratte. Se un oggetto all'interno della varietà si muove verso la parete di fronte, sparisce attraverso quella parete e riappare dalla parete dietro le spalle: analogamente, l'oggetto sparisce attraverso la parete di destra e riappare dalla parete di sinistra; sparisce nel soffitto e riappare dal pavimento. Evidentemente questo moto è molto simile al moto di un oggetto interno al toro: la varietà è l'analogo tridimensionale del bitoro e perciò viene chiamata tritoro. In questo modo,se momentaneamente mettiamo da parte il concetto di spazio reale fisico, in tal modo possiamo facilmente immaginare come si vivrebbe in un tritoro. Per ultimo diamo un esempio intuitivo di una tri-varietà astratta, una delle più quotate per interpretare la forma dell'universo.
La tri-varietà di Herbert Seifert e C. Weber
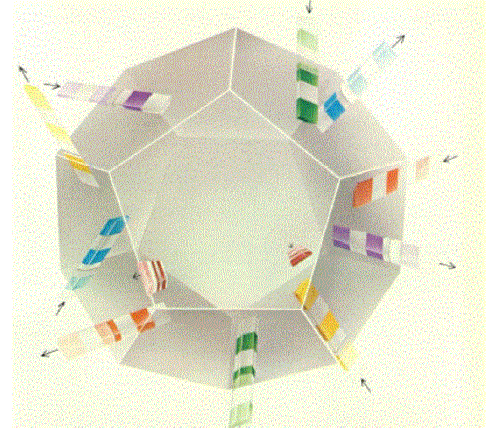
Un modello possibile per la topologia dello spazio è la trivarietà scoperta nel 1932 da Herbert Seifert e C. Weber. La possiamo rappresentare solo in modo astratto, non avendo a disposizione 4 o 5 dimensioni. Consideriamo il dodecaedro in figura e identifichiamo ogni faccia con la sua opposta ruotata di tre decimi di un angolo giro. In questo caso tutti i vertici sono identificati e formano un'unica classe di equivalenza; per quanto riguarda i lati, questi sono invece raggruppati in 6 classi distinte. Quando parleremo della geometria delle varietà (congettura di Thurston), vedremo meglio perchè lo spazio possa essere rappresentato da tale varietà. Ma .. un passo alla volta. Nel prossimo articolo affineremo la struttura delle varietà topologiche, introducendo le varietà differenziabili.
Gli altri articoli di questa serie:





