Abbiamo visto che gli urti tra due masse e di una di loro contro una parete riesce a regalarci le cifre significative del pi greco. Analizziamo a fondo il perché, anche se Francesco ha già dato una risposta esauriente. Ci troviamo di fronte a un problema puramente matematico espresso attraverso la meccanica e dimostrabile con la semplice geometria. Un gran bell'esempio di interdisciplinarità.

Iniziamo, descrivendo ciò che capita, in modo puramente qualitativo...

La massa m1 si muove, all'inizio, verso sinistra, per cui la sua velocità è negativa ed è posta uguale a -1. La massa m2 è ferma.  Le due masse si urtano conservando sia l'energia totale del sistema formato dalle due masse sia la quantità di moto. Il passo successivo è il moto di m2  verso la parete (velocità negativa) e l'urto contro di essa. La massa m1 si muove anch'essa verso la parete, ma con velocità ridotta rispetto all'inizio. Quando m2 urta contro la parete la sua velocità cambia solo di segno. Questo fatto vuol dire che l'energia cinetica del sistema delle due masse non è assolutamente cambiata, in quanto la velocità compare al quadrato. E' invece cambiata la quantità di moto, dato che la velocità di m2 ha cambiato di segno. Abbiamo ora le due masse che viaggiano una verso l'altra (m1 con velocità negativa e m2 con velocità positiva): l'urto è inevitabile ed esso deve conservare sia la quantità di moto sia l'energia cinetica. Ciò implica che la massa m2 torni verso la parete, mentre la massa m1 continui nel suo moto verso sinistra con velocità ridotta. Il gioco continua fino a quando?

Dopo un certo numero di scontri, la velocità della massa m1  inverte il suo segno e inizia ad andare verso destra (verso positivo). Tuttavia, m2 colpisce ancora la parete, tornando indietro con un valore della velocità positiva come quella di m1, ma ancora sufficiente a colpirla.  Il gioco finisce quando la velocità v2 di m2 non è più  sufficiente a raggiungere  m1. Questa conclusione viene raggiunta quando v2  e v1 sono entrambe positive ma v1 è maggiore di v2.

Tante belle parole, ma vediamo di applicarle a un caso pratico, corredato dalle figure essenziali per seguirlo completamente in modo quantitativo...

Iniziamo con un esempio che chiarisca per bene la successione degli eventi.

Consideriamo il caso in cui m1 = 10 e m2 = 1. Un caso che non è contemplato tra quelli utili al nostro scopo, ma che può spiegare molto bene cosa e come avviene. Non spaventatevi dei numeri, soprattutto quelli relativi alla quantità di moto Q. Ho inserito numeri approssimati a causa dei troncamenti sulle velocità. Ciò che è indispensabile ricordare è che ad ogni urto tra le masse la quantità di moto del sistema formato dalle due masse non deve cambiare. Ovviamente, non deve cambiare nemmeno l'energia cinetica totale.  Nell'urto contro la parete le cose cambiano... e' solo m2 ad essere coinvolta e ciò che capita è che deve conservarsi la quantità di moto del sistema massa e parete. Il che significa che la velocità di m2 deve cambiare di segno. A questo punto, la quantità di moto del sistema due masse non può più essere uguale ed è costretto a cambiare a causa del cambiamento di segno della velocità di m2. Non cambia, invece, l'energia totale delle due masse dato che la velocità compare al quadrato.

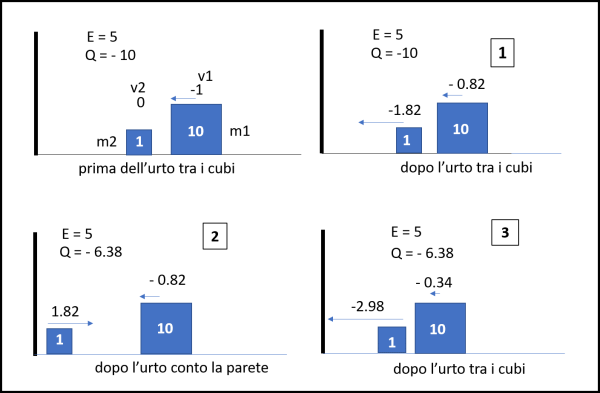
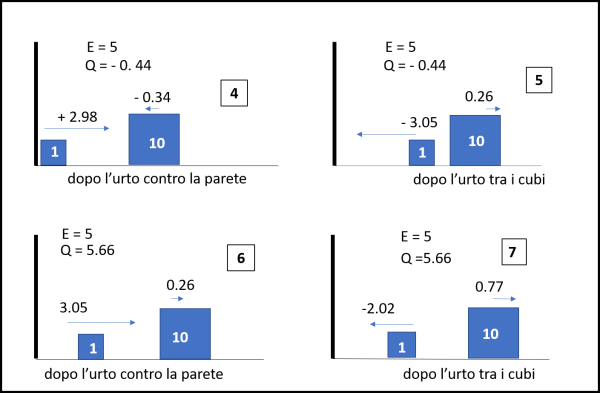
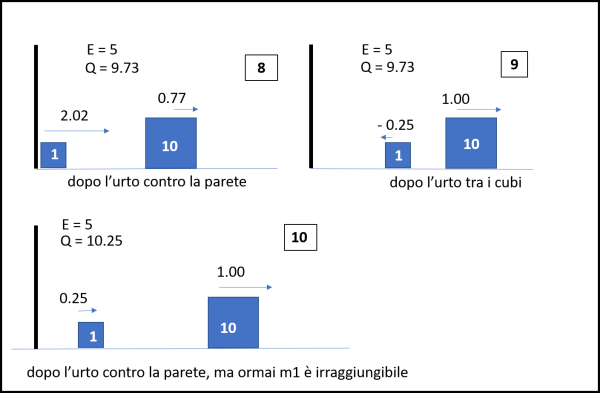
Riassumendo: ad ogni urto tra le masse si conservano sia l'energia totale sia la quantità di moto. Ad ogni urto contro la parete si conserva l'energia, ma non  la quantità di moto. Nel caso di m1 = 10 e m2 = 1, la successione degli eventi è rappresentato nelle Fig. 1 che corrisponde ai dieci urti totali. La prima immagine ci porta all'inizio, prima del primo urto. Dopo di che le altre immagini si riferiscono ai singoli urti. Sono indicate le velocità prima e dopo gli urti, l'energia totale E e la quantità di moto totale Q.

Figura 1

E e Q soni dati da:

E = 1/2 m1v1² + 1/2 m2v2²               che rimane sempre la stessa essendo indipendente dal segno delle velocità.

Q = m1v1 + m2v2           che cambia  ogni volta che m2 urta la parete, ma rimane costante nell'urto tra le masse.

Le due relazioni permettono di ricavare le velocità dopo gli urti (come è stato riportato nelle figure), ma è veramente necessario per il nostro scopo? No, non è assolutamente necessario, ricordando che a noi interessa solo il numero degli urti. Le uniche variabili nel nostro problema sono proprio le due velocità v1 e v2, per cui non è certo difficile costruire il luogo dei punti in cui l'energia totale si mantiene sempre costante (per ogni singolo caso, m1 e m2 sono costanti).

Possiamo, allora, prendere come ascissa la velocità v1 e come ordinata la velocità v2.

Nel caso precedente (m2 = 10), otteniamo, fin dall'inizio, la relazione per l'energia che rimane sempre la stessa:

E = (10/2) (-1)²  + (1/2) · 0² = 5

Ossia, le velocità dovranno sempre trovarsi lungo questa curva:

1/2(10 v1² + 1 v2²) = 5

5 v1² + v2²/2 = 5

v1² + v2²/10 = 1

Ma questa è l'equazione di un'ellisse con centro C nell'origine (v1 = 0, v2 = 0) e semiassi a = 1 e b = √10 (ricordiamone la formula generale: x²/a² + y²/b² = 1)

Non è difficile disegnarla in Fig. 2.

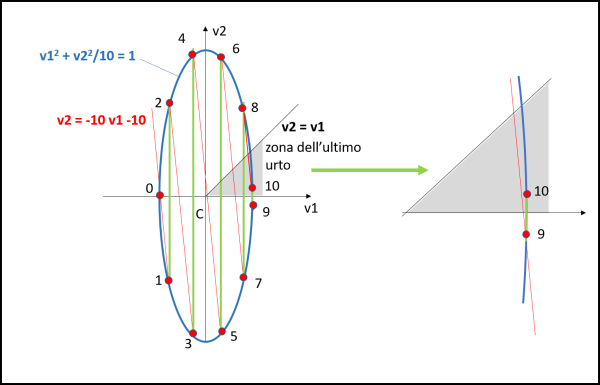
Il punto 0 (pallino rosso) è relativo a un attimo prima dell'urto iniziale, infatti abbiamo v1 = -1 e v2 = 0. Dopo il primo urto il pallino rosso, ossia l'energia cinetica totale, può trovarsi in qualsiasi punto dell'ellisse, dato che ogni suo punto corrisponde alla stessa energia cinetica. Tuttavia, noi abbiamo in mano una carta in più, ossia la quantità di moto che dopo il primo urto deve mantenersi costante.

La sua espressione è data da:

m1v1 + m2v2 = Q

-10 · 1  + 1· 0 = -10

L'equazione:

10 v1 + v2 = -10

corrisponde al luogo dei punti che hanno la stessa quantità di moto dopo il primo urto tra le due masse. Scriviamola meglio...

v2 = - 10 v1 - 10

questa è una retta con coefficiente angolare -10 che passa per il punto 0 (infatti: per v2 =0, abbiamo v1 = -1). Il sistema delle due masse dopo il primo urto si deve trovare sia sulla retta che indica la quantità di moto costante (retta rossa) sia in un punto dell'ellisse. Ciò vuol dire che l'unico punto possibile è il punto 1, intersezione tra la retta e l'ellisse. In realtà, ciò che capita dopo il primo urto è rappresentato dal tratto inclinato tra 0 e 1 lungo la linea rossa.

Nel punto 1 avviene l'urto tra la massa m2 e la parete. Quale sarà il punto corrispondente sull'ellisse che rappresenta la costanza dell'energia? Presto detto: il punto 2. Infatti, dopo l'urto la velocità v2 cambia di segno, ma deve restare sull'ellisse a energia costante. Questa situazione porta a una nuova quantità di moto che deve, però restare immutata dopo l'urto tra le masse fino al successivo urto di m2 contro la parete. L'urto contro la parete è, perciò, raffigurato dal tratto verticale verde tra 1 e 2.

Notiamo adesso che, pur variando la quantità di moto totale, a causa del cambio di segno di v2, il coefficiente angolare  della retta(che dipende solo dalle due masse) non cambia. Il che vuol dire che traslando la retta nel punto 2 dell'ellisse, otteniamo la nuova retta rossa, parallela alla prima, che impone una quantità di moto costante. Il punto dove questa retta incontra nuovamente l'ellisse è il punto 3, relativo al nuovo urto di m2 contro la parete. Nuova linea verticale verde che cambia di segno a v2 e via  dicendo. Dal punto 9 al punto 10 si ha l'ultimo urto  contro la parete, con il corrispondente cambiamento di segno  di v2 . Tuttavia, dopo questo nuovo urto (10), la v2 è positiva ed è minore di v1 (abbiamo tracciato la retta v2 = v1, per rendere chiara la zona interessata). A questo punto non vi può più essere nessun urto, dato che m1 scappa più velocemente di m2 e vanno entrambe in verso positivo. Il numero di urti è quindi pari a 10.

Bene... una  bella descrizione geometrica di un processo di meccanica classica, già molto interessante di per sé, ma... cosa c'entra con il pi greco? Sappiamo che le sue cifre significative sono proprio uguali  al numero di urti, per masse scelte ad hoc, ossia seguendo la legge m1 = 100^d-1 con d intero e crescente, ma perché venga fuori proprio il solito numero, che appare in quasi ogni angolo della matematica (e non solo), rimane ancora un mistero.

Se avessimo  un cerchio invece dell'ellisse, il tutto sarebbe molto più utile dato che la  circonferenza vale proprio 2πr e gode di tante bellissime proprietà che potrebbero venirci utili.In poche parole, sarebbe bello trasformare la nostra ellisse in un cerchio e ripetere l'esercizio di prima. Sarebbe bello e ... anche piuttosto facile. Riprendiamo l'equazione che ci ha regalato l'ellisse e studiamola un pochino...

E = 1/2(m1v1² + m2v2²)

Proviamo a scriverla in questo modo:

E = 1/2 (√m1 v1 √m1 v1 + √m2 v2 √m2 v2)

Poniamo adesso:

√m1 v1 = x

√m2 v2 = y

L'equazione dell'energia diventa:

E = 1/2 (x² + y²)

x² + y² = 2E

Nel caso di m1 = 10, avremmo:

x2 + y2 = 10

Un cerchio con il  raggio uguale a √10.

In pratica l'ellisse precedente verrebbe "stirata" lungo l'asse x in modo che il raggio diventi uguale all'asse b.

D'altra parte il cambiamento di coordinate non ha cambiato l'ordinata in quanto

y = √m2 v2 = √1 v2 = v2

mentre

x = √1o v1

La Fig. 3 ci mostra come si trasformi l'ellisse precedente. La y iniziale rimane uguale alla v2 e quindi uguale a zero, mentre la x iniziale vale ora - √10.

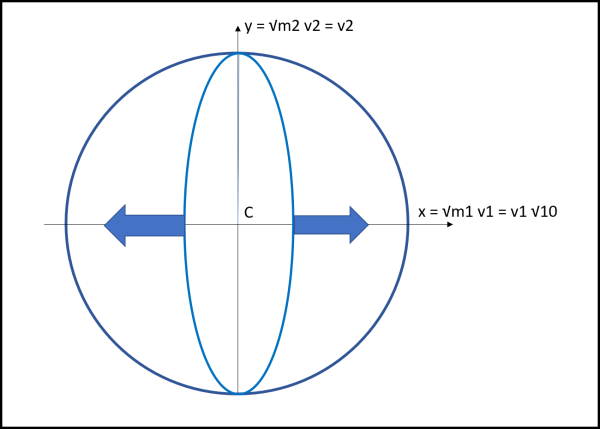
La stessa trasformazione deve interessare anche la retta inclinata che rappresenta la quantità di moto.

v1m1 + v2m2 = Q

v1√m1 √m1 + v2 √m2 √m2 = Q

Nel caso di m1 = 10, abbiamo:

x√m1 + y√m2 = -10

y = - x √m1/√m2 -10/√m2

y = - x √10 - 10

Il nuovo coefficiente angolare è ora - √10

Per y = o vale ovviamente x = -10/√10 = - √10

Possiamo ora, in Fig. 4, ripetere il procedimento fatto per l'ellisse sulla sua trasformazione in cerchio.

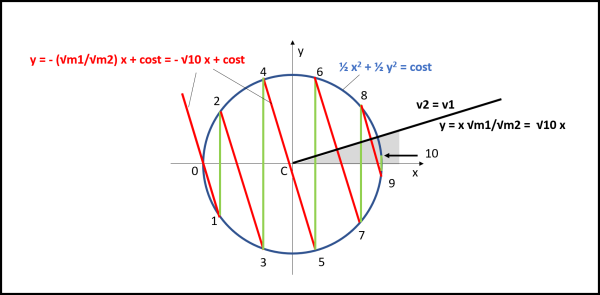
La cosa più importante, come già detto, è che adesso conosciamo bene quanto vale l'arco completo della circonferenza, ossia 2π.

Facciamo qualche considerazione molto importante, utilizzando la Fig. 5

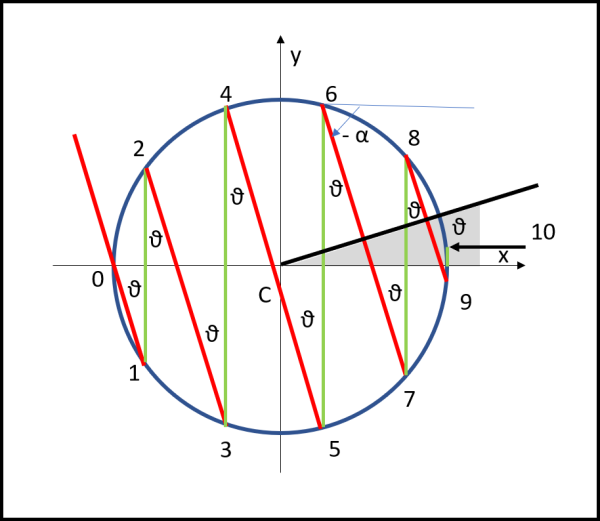
Innanzitutto vediamo che tutti gli angoli θ sono uguali fra loro, in quanto angoli alterni interni di rette parallele  (quelle verdi verticali) tagliate da una trasversale (retta rossa).

Possiamo anche facilmente sapere quanto vale l'angolo θ. La retta rossa ha coefficiente angolare

tan(- α) = - tan (α) = - √m1/√m2 = - √10

Ma θ non è altro che 90 - α, e possiamo scrivere:

tan(θ) = tan(90 - α) = 1/tan(α) = √m2/√m1 = 1/√10

θ = atan(√m2/√m1) = atan(1/√10) = 0.306 rad

Altro fatto molto importante da ricordare è che l'angolo alla circonferenza è sempre metà dell'angolo al centro.

In Fig. 6 possiamo notare che l'arco tra 1 e 3 sottende un angolo al centro che vale 2θ e, quindi,  l'arco stesso vale 2θ radianti.

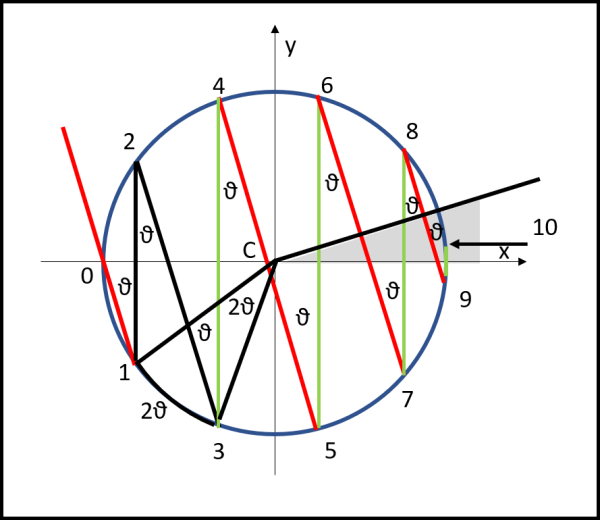
Non è certo difficile dimostrare che anche l'arco 0-2 è pari a 2θ (Il segmento 2-0 forma lo stesso angolo θ con il segmento 2 -1 e, quindi, 1 - 0 = 2 - 0)

Tutti gli archi 0 - 1, 0 - 2, 1 - 3, 2 - 4, 3 - 5, 4 - 6, 5 - 7, 6 - 8, 7 - 9, 8 -10  sono uguali a 2θ. Per raggiungere la circonferenza manca ancora il pezzetto di arco 9 - 10 che non può essere contato in quanto 10 cade all'interno del triangolo grigio dove non è più possibile nessun urto.

Possiamo finalmente eliminare rette rosse e verdi e considerare soltanto gli archi uguali a 2θ, come riportato in Fig. 7.

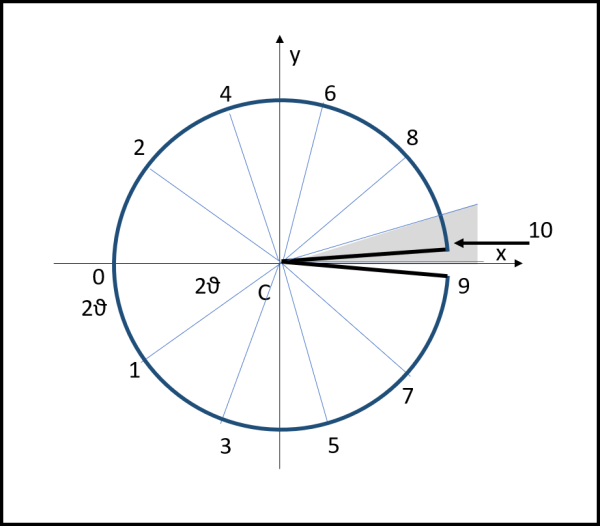
Notiamo un fatto estremamente importante: il numero di 2θ che sono stati sommati è il numero massimo possibile perché non si superi il valore di 2π. Infatti se ne aggiungessimo un'altro nel punto 10, andremmo oltre il punto 9 e supereremmo il valore di 2π. E questo fatto vale, ovviamente, per tutti i valori che volessimo scegliere per m1,  la grandezza fondamentale per sapere quanti urti si effettuano, che equivale al numero di archi 2θ.

Manteniamoci ancora nel caso di m1 = 10 e arriviamo fino in fondo...

Il numero di urti è 10 e tanti sono anche gli archi 2θ che vanno sommati per ottenere un valore finale inferiore a 2π.

Possiamo allora scrivere:

10 2θ < 2π

10 θ < π     ..... (1)

Sappiamo che θ = 0.306 rad, da cui otteniamo

3.06 < π

Il che è senz'altro vero, così come è senz'altro vero che se aggiungessimo un altro θ, otterremmo

3. 06 + 0.306 = 3.366 > π

Bene... molto bene... ma 3.06 non è certo una gran bella approssimazione per π. La cosa migliore da fare è saper scegliere le masse m1 che comportino veramente la conoscenza delle cifre significative del celebre numero!

Riscriviamo la (1) per il caso generale, ricordando che θ = atan (1/√m1) essendo m2 sempre uguale a 1.

N θ < π

N atan(1/√m1) < π         .... (2)

Facciamo una piccola tabella che riporti la massa m1 e il corrispondente valore di θ = atan (1/√m1) in radianti.

Possiamo notare che siamo di fronte ad angoli piccolissimi e che possiamo tranquillamente sostituire ai valori di θ i valori "approssimati"  0.1, 0.01, 0.001, 0.0001, 0.00001.

La formula precedente (2) porta ai valori di N per ogni singolo caso

31 · 0.1 = 3.1 < π  = 3.14159265

314 · 0.01 = 3.14  < π  = 3.14159265

3141 · 0.001 = 3.141 < π  = 3.14159265

31415 · 0.0001 = 3.1415 < π  = 3.14159265

314159 · 0.00001 = 3,14159 < π  = 3.14159265

I numeri interi massimi N, trovati per non superare il valore di π, sono esattamente gli urti tra le masse m1 e m2 al variare della massa m1 con la legge m1 = 100^d-1.

Se aggiungessimo un numero intero a N troveremmo un valore sempre maggiore di π. Questo capiterebbe anche considerando il valore esatto di θ. Proviamo nel caso della massa m1 = 10 000.

314 · 0.009999667 = 3.1398953396 < 3.14159265

315 · 0.009999667 = 3,1498950063 > 3.14159265

La stessa cosa succede approssimando θ con 0.01

314 · 0.01 = 3.14 < 3.14159265

315 · 0.01 = 3.15 > 3.14159265

In poche parole, l'approssimazione eseguita su θ non influisce sul numero N, ossia il numero di urti regala di volta in volta una cifra significativa al nostro caro amico pi greco.

Beh... è stata un po' faticosa, ma estremamente interessante e istruttiva. Ancora bravo al nostro Francesco!