Un genio autodidatta assoluto: Ramanujan ** (con risposta finale)
Questo articolo è inserito in Matematica e Geometria
L’autore del libro “The man who knew infinity”, da cui fu tratto il film “L’uomo che vide l’infinito” del 2015, disse di lui: "Ramanujan fu un matematico così grande che il suo nome trascende le gelosie, il più superlativamente grande matematico che l'India abbia prodotto nell'ultimo migliaio di anni. I suoi balzi di intuizione confondono i matematici ancor oggi, sette decenni dopo la sua morte. I suoi scritti sono ancora scandagliati per i loro segreti. I suoi teoremi sono applicati oggi in aree difficilmente immaginabili quando era in vita." Ricordiamo, in particolare, l'utilizzo delle sue idee innovative anche nel campo della termodinamica dei buchi neri e nella teoria delle stringhe.
Nato in un villaggio indiano nel 1887, visse un’infanzia di grande povertà e iniziò a dedicarsi alla matematica fin da giovanissimo, benché non riuscì mai a completare studi specialistici. Anche se la sua abilità nel proporre teoremi del tutto nuovi e ritrovare, secondo metodologie diverse, le espressioni fondamentali della matematica superiore (a lui del tutto sconosciute), cominciò a essere nota in Patria, ottenne scarsi risultati riguardo alla sua possibile ammissione alle Università. Tutto o quasi è stato riportato nei suoi taccuini, dove le dimostrazioni non erano quasi mai riportate essendo per lui praticamente ovvie. Un genio quasi completamente autodidatta. Trovò lavoro come contabile, finché non decise di scrivere a un famoso matematico inglese, G.H.Gardy.
La sua lettera era molto semplice e - probabilmente- poco credibile: "Caro Signore, mi permetto di presentarmi a voi come impiegato presso il Dipartimento conti dell’Ufficio portuale di Madras con uno stipendio di sole 20 sterline all’anno. Ora ho circa 23 anni di età. Non ho alcuna formazione universitaria ma ho seguito i corsi delle scuole ordinarie. Dopo aver lasciato la scuola, ho speso il mio tempo libero a lavorare in matematica. (…) sto seguendo un nuovo percorso da me stesso. Ho studiato le serie divergenti e ho ottenuto risultati che i matematici locali definiscono sorprendenti",
Alla lettera, però, allegò alcuni suoi studi e soluzioni del tutto sconosciute a quei tempi. Hardy non poté che esserne incuriosito e anche sconvolto. Dopo un primo momento di perplessità, Hardy e altri colleghi inglesi capirono di trovarsi di fronte a un genio senza precedenti, del tutto autodidatta.
Alcuni dissero: "Era estremamente difficile parlare con lui: ogni volta che si menzionava qualche soggetto che si pensava che Ramanujan avesse bisogno di conoscere, lui proponeva una valanga di idee originali che rendevano quasi impossibile persistere nelle intenzioni originali di insegnamento della matematica classica.".
Hardy ebbe a dire: Un matematico di altissima qualità, di originalità e forza del tutto eccezionali, che può essere confrontato solo con Eulero o Jacobi”
Con l'aiuto di Hardy riuscì a ottenere la laurea a Cambridge, malgrado non avesse i titoli necessari per esserne ammesso e, su spinta dei massimi matematici del tempo, venne inserito tra i membri della Royal Society di Londra. Tuttavia, Ramanujan era già malato di tubercolosi e si era all’inizio della prima guerra mondiale. Fu costretto a tornare in India dove morì a 33 anni.
Invito tutti a leggere di più attorno alla sua vita (ad esempio QUI) o a vedere il film. Qui voglio limitarmi a una sua "semplice" sommatoria che è stata utilizzata nel titolo della celebrazione del 120esimo anniversario della sua nascita (1887):
Ovviamente, la sommatoria del titolo è uguale a 120.
Analizziamo meglio e più in generale quella strana formula. Ricordiamo, a tal proposito, che quando era ancora in India, aveva proposto ai matematici della sua Nazione, attraverso il Journal of the Indian Mathematical Society, una specie di indovinello, chiedendo il risultato delle seguenti due espressioni:
Nessuno fu in grado di rispondere ed egli fornì la risposta dopo sei mesi.
Bene. Cerchiamo di divertirci anche noi... Cominciamo con la prima espressione, un caso particolare, ma dal risultato inaspettato.
Scriviamolo con qualche termine in più:
In questo caso è facile partire dal risultato e dimostrare con semplici passaggi la sua validità:
x vale 3
Controlliamo passo dopo passo, partendo da 3. Possiamo scrivere:
e via così fino a quando si vuole. Aggiungendo un nuovo termine il risultato non cambia mai e vale sempre 3 come fin dal primo passaggio. Fantastico!
Per provare che il risultato non cambia mai, basta provare che il termine generico è identico al termine generico successivo, ossia che:
Ma questo è un gioco veramente banale...
Che si identifica perfettamente con:
f(n) = 1 + n
Nel nostro caso, con n = 2, si ha:
f(2) = 3 = 1 + 2
Nel caso del titolo della celebrazione n = 119 e quindi:
f(n) = 1+ 119 = 120
Per chi ha voglia di divertirsi ancora un po'...
In realtà la formula completa di Ramanujan è più complicata e necessita di tre parametri:

Attenzione: la x è adesso la n di prima, mentre n è un numero intero come a.
La formula ridotta precedente si ottiene con n= 1, a = 0 e x = 2 e va riscritta come:
f(2) = n + a + x = 1 + 0 + 2 = 3
Utilizzando la formula completa possiamo dare il risultato del secondo indovinello posto sul giornale da Ramanujan, ossia l'espressione:
Divertitevi da soli e trovate il valore dell'espressione e, ovviamente, i valori di x, n e a...
Soluzione:
Confrontando l'ultima espressione con quella generale, possiamo subito dire che
x = 2 (fattore che moltiplica le radici)
n = 1 (incremento del valore di x)
Non ci resta che trovare a.
Basta considerare il termine ricorrente generico e confrontarlo con quello del quiz:
ax + (n + a)2 = 6
ponendo x = 2 e n = 1 abbiamo:
2a + (1 - a)2 = 6
2a + 1 + a2 + 2a - 6 = 0
a2 + 4a -5 = 0
risolvendola si ha:
a = - 2 +/- √(4 + 5) = - 2 +/- 3
Accettando il valore positivo, abbiamo:
a = - 2 + 3 = 1
Bravo MarcoC !!!
QUI continuiamo a parlare di Ramanujan



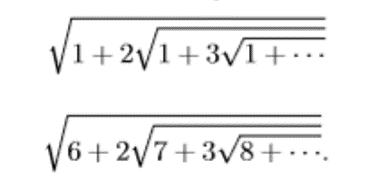
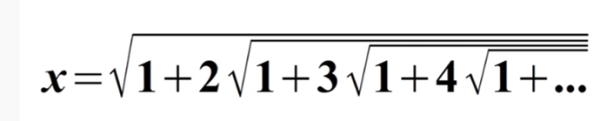
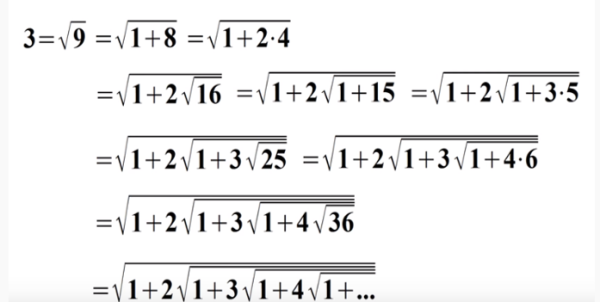
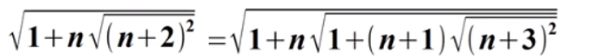
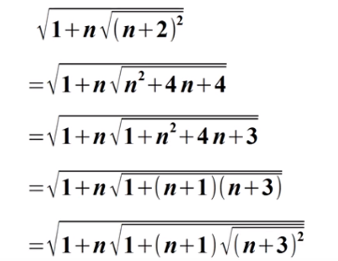
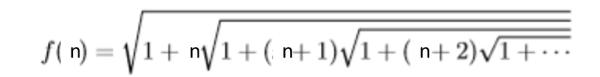
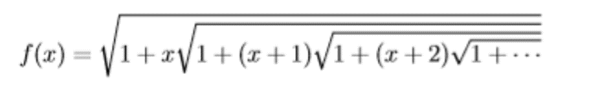





4 commenti
Non ne avevo mai sentito parlare.
Proverò anche a vedere il film perchè mi sembra una storia molto interessante.
Grazie.
caro MarcoC,
il film è ovviamente molto romanzato, ma la storia merita di essere conosciuta a fondo. Un genio veramente incomprensibile!!! Tanto che ci sei... dammi anche la risposta alla domanda finale....
Proviamo:
a=1
n=1
x=2
F ()=4
bravo!!!