Categorie: Matematica
Tags: asse bisettrice dolcetto scherzetto triangoli equilateri triangoli isosceli triangoli scaleni triangoli uguali
Scritto da: Vincenzo Zappalà
Commenti:8
Dolcetto o scherzetto? *
No, non mi sono adattato a una festa puramente consumistica, ma approfitto della data per proporvi un semplicissimo scherzetto matematico (ma è davvero uno scherzetto o c'è qualcosa di più profondo?).
Disegniamo un triangolo scaleno qualsiasi ABC nella figura che segue
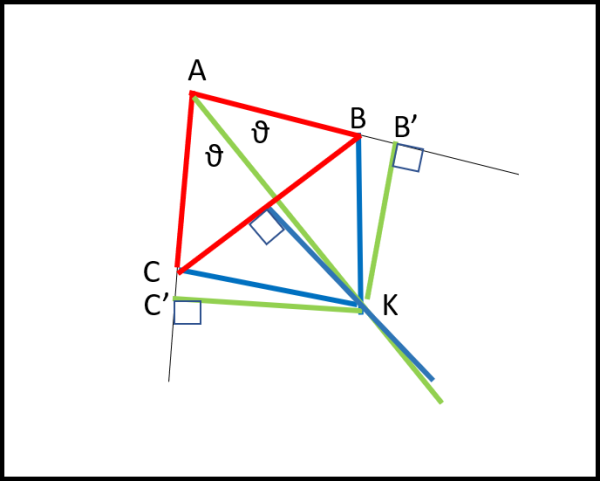
Tracciamo la bisettrice dell'angolo BAC (verde) e l'asse del lato BC (blu). Esse si incontrano nel punto K. Tracciamo le congiungenti K con B e C. KB deve essere uguale a KC dato che K appartiene all'asse di BC. Tracciamo le perpendicolari da K alle rette AB e AC e troviamo i punti B' e C'. Anche KC' = KB' dato che K appartiene alla bisettrice.
Ne segue che i triangoli rettangoli KBB' e KCC' sono uguali, dato che hanno due lati uguali. Possiamo perciò scrivere:
BB' = CC'
Consideriamo adesso i triangoli AC'K e AB'K. Anche essi sono uguali, essendo rettangoli e avendo due lati uguali. Possiamo allora scrivere:
AB' = AC'
Scriviamo le espressioni:
AB = AB' - B'B
AC = AC' - CC'
Ma, AB' = AC' e B'B = CC', per cui
AB = AC.
Se ne deduce che il triangolo ABC è isoscele...
Potremmo ripetere la costruzione per gli altri due angoli del triangolo ABC (abbiamo scelto un suo angolo a caso) e trovare che tutti lati sono uguali e che quindi il triangolo ABC è addirittura equilatero!
Scherzetto o ... dolcetto?
Soluzione QUI






8 commenti
Forse l'errore è qui "Ne segue che i triangoli rettangoli KBB' e KCC' sono uguali, dato che hanno due lati uguali."
L'angolo uguale dovrebbe essere quello compreso tra i lati uguali.
caro MarcoC,
se due triangoli sono rettangoli e hanno uguali l'ipotenusa e un cateto devono essere uguali. D'altra parte l'altro cateto lo trovi con Pitagora e il risultato dà proprio che BB' = CC'
Opss.... è vero. Mi cospargo il capo cenere.
ma che sia cenere fredda...
Diciamo imbroglietto: ho tracciato un po' di triangoli scaleni. A me risulta sempre che quando traccio le rette dal punto di intersezione tra la bisettrice e l'asse del lato opposto, perpendicolari ai due lati del triangolo, l'intersezione una volta è all'interno del lato, una volta all'esterno (stiamo parlando dei punti B' e C').
Quindi, quando riscrivi AB e AC, una è differenza tra i due segmenti trovati, l'altra è la somma
Per completezza adesso mi tocca spiegare il perché
vorresti dire che non ho fatto bene il disegno?
Forse hai proprio ragione...
Pensa all'anello,,, tu ce la puoi fare di sicuro, anche con l'astronave talpona...
caro Francesco,
per provarlo puoi sempre prendere un triangolo rettangolo (deve poter capitare per ogni triangolo...) e bastano poche considerazioni...