Questo articolo è stato inserito nella pagina di approfondimento dedicata alla Meccanica Celeste.

 

Questo articolo riunisce le varie puntate relative alla lezione "persa" di Feynman, in cui riesce a ricavare le leggi  di Keplero basandosi soltanto sulle leggi di Newton. Il tutto senza nemmeno un'equazione differenziale, ma solo giocando su triangoli uguali e su un diagramma geniale. Una trattazione talmente elegante e semplice che deve essere patrimonio della conoscenza di chiunque abbia vera passione per la fisica.

Basterebbe leggere questo articolo per capire quanto sia complicato ricavare le leggi di Keplero attraverso la legge di gravitazione di Newton. Beh... Feynman riesce a giungere allo scopo con costruzioni che in parte si rifanno allo stesso Newton e in parte sono dovute al suo genio. Ne deriva una specie di avventura, di estrema semplicità, che non può che stupire e appassionare.

Introduzione

Nel marzo del 1964, Richard Feynman tenne una lezione a dir poco “storica”. L’argomento era quanto di più interessante si potesse desiderare: “Il moto dei pianeti intorno al Sole”. Una lezione che lo stesso Feynman disse ai suoi allievi di aver preparato “soltanto per il piacere di farla e per il vostro divertimento”. Il divertimento per Richard era sempre molto particolare e si riferiva ad argomenti estremamente ELEMENTARI (ossia fondati su basi da liceo), ma non era veramente SEMPLICE, dato che abbisognava di una buona dote di INTELLIGENZA.  La lezione e soprattutto le figure originali sono in gran parte andate perse, ma un suo collega ha ricostruito il contenuto della lezione che può essere seguita da chiunque abbia anche solo un vago ricordo della geometria euclidea. E' proprio ciò che faremo noi (o, almeno cercheremo di fare) cercando di semplificare e di estendere ancora di più le parti più “critiche” e fondamentali.

Feynman prende le mosse dall'osservazione di Keplero sul moto dei pianeti intorno al Sole lungo orbite ellittiche e dal fatto che un segmento che congiunge un pianeta al Sole 'spazza' aree uguali in tempi uguali. Rifacendosi a Newton ricorda anche che l'uguaglianza delle aree in tempi uguali è equivalente all'affermazione che la forza varia secondo l'inverso del quadrato della distanza. Ma ciò che emoziona di più è la scoperta che la prima legge di Keplero è una conseguenza delle altre due (una sintetica spiegazione delle leggi di Keplero la trovate QUI).

Una volta stabilito che la forza è diretta verso il Sole e che varia secondo l'inverso del quadrato della distanza, Newton riuscì a elaborare le combinazioni tra velocità e variazioni di velocità, e mostrare che essa era un'ellisse, usando sofisticati e un po’ contorti metodi legati alle molteplici caratteristiche delle “sezioni coniche”. Lo stesso Feynman, con la sua solita ironia, ammette di fare “fatica” a seguirle tutte.  Decide, allora, di elaborare una geniale dimostrazione ELEMENTARE (col particolare significato datogli prima).

Un insieme di raffinati “trucchi” geometrici che superano tutti gli scogli incontrati da Newton nella sua dimostrazione basata sulle sezioni coniche. Insomma… uno dei tanti piccoli-grandi capolavori di Richard.

Iniziamo dalla fine e poi chiuderemo il... cerchio (anzi l'ellisse!).

Il colpo di teatro

Consideriamo un cerchio di raggio R, con centro in C. Non ci resta che prendere un punto P qualsiasi all’interno della circonferenza.

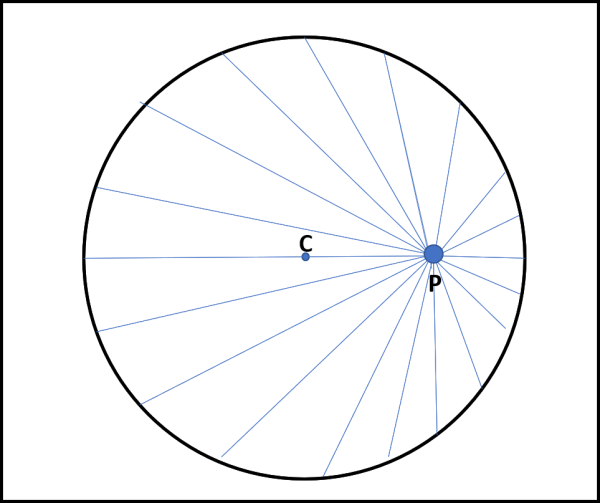
Utilizziamo, prima, la versione puramente grafica e di grande effetto. Dal punto P tracciamo un gran numero di segmenti rettilinei (al limite anche infiniti), che vadano a toccare la circonferenza, come mostrato in Fig. 1.

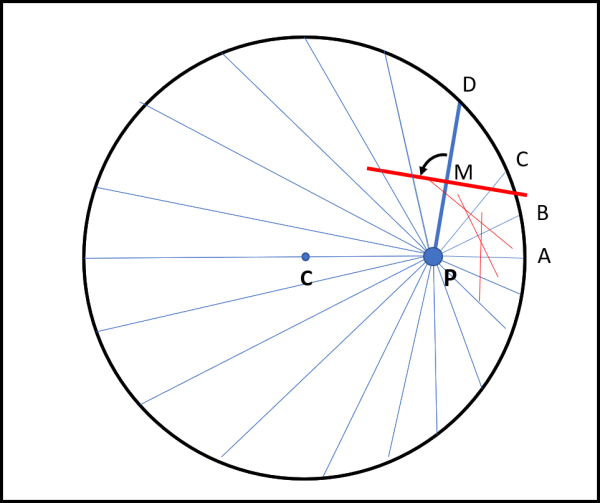
Per ogni segmento fissiamo il punto di mezzo e ruotiamo ciascun segmento di 90° attorno a questo punto, come iniziato a fare in Fig. 2 e, in particolare, per PD.

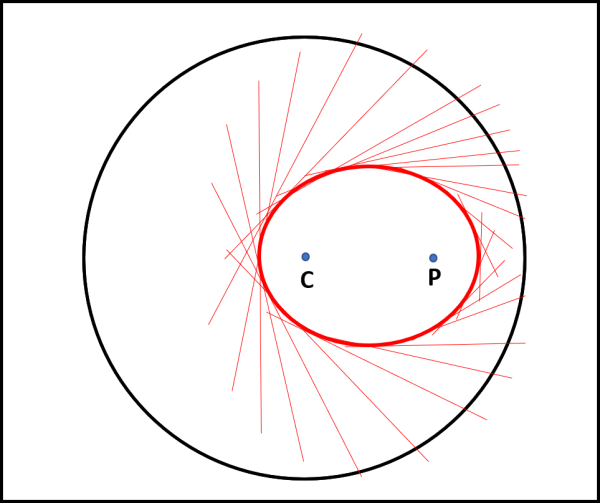
Completata la nostra “manovra”, possiamo tranquillamente eliminare i segmenti iniziali e lasciare solo quelli ruotati di 90°: quello che ci appare è una perfetta ellisse, inviluppo dei segmenti ruotati (Fig. 3).

Ovviamente, la messa in scena è ancora più emozionante se i segmenti sono in numero molto grande, come si vede nella fig. 4, in cui è rappresentato l’inizio, un momento intermedio e il finale dello spettacolo.

La costruzione geometrica

“Sì”, mi dirà qualcuno, “la curva è molto bella e assomiglia a un’ellisse con P e C nei due fuochi… ma è proprio un’ellisse? Sarebbe meglio avere una prova definitiva!”. E noi (ossia Feynman) non ha nessuna difficoltà a darla in modo veramente elementare.

Utilizziamo la Fig. 5, dove PA è un qualsiasi segmento originario.

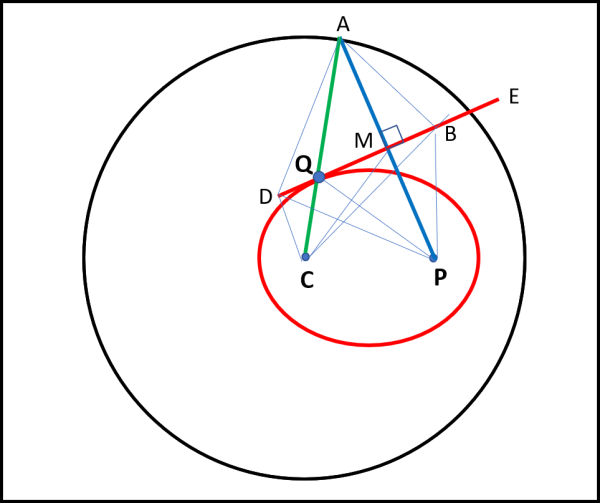
Sia M il suo punto di mezzo e DE il corrispondente segmento ruotato di 90° attorno al punto M. Qualsiasi punto del segmento DE gode di una banale proprietà: esso ha distanza uguale da A e da P. Infatti, ogni triangolo rettangolo del tipo ABM è uguale al suo fratello BMP, avendo il cateto MB in comune e il cateto AM uguale a MP per costruzione. Consideriamo un punto particolare sul segmento DE, ossia quello che sta sul raggio CA. Anche per lui ovviamente vale la relazione:

AQ = QP

Da cui segue che:

CA = CQ + AQ = CQ + QP = R

Il raggio R è ovviamente una costante, per cui la relazione precedente ci dice che la somma delle distanze di Q da C e da P è una costante. Dato che lo stesso procedimento si può fare per qualsiasi segmento iniziale, il punto Q descrive il luogo dei punti che hanno la somma delle distanze da due punti fissi uguale a costante. In altre parole: il punto Q descrive un’ellisse di fuochi P e C.

Fantastico, veramente fantastico.  Per non farci mancare niente utilizziamo l'animazione preparata rapidamente da Arturo (Fig. 6), che mostra l'intera costruzione.

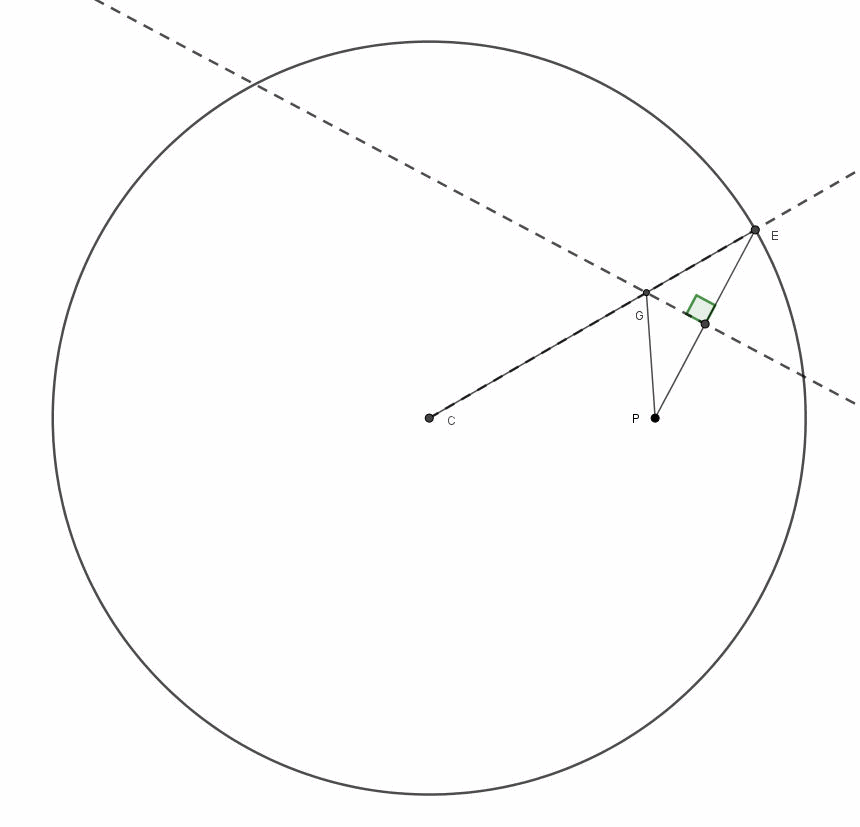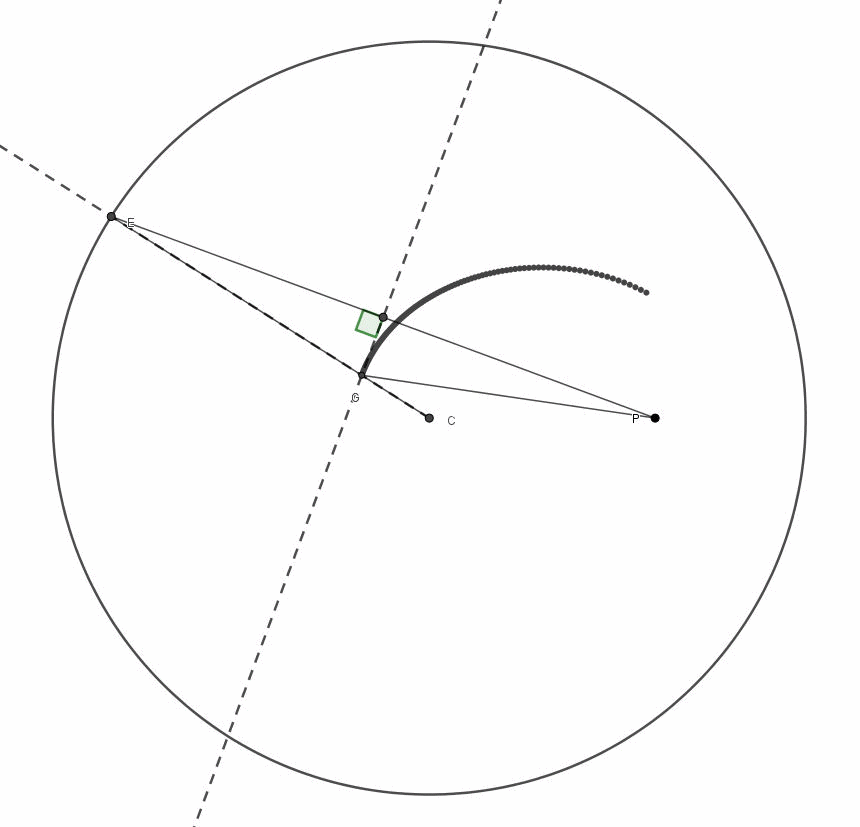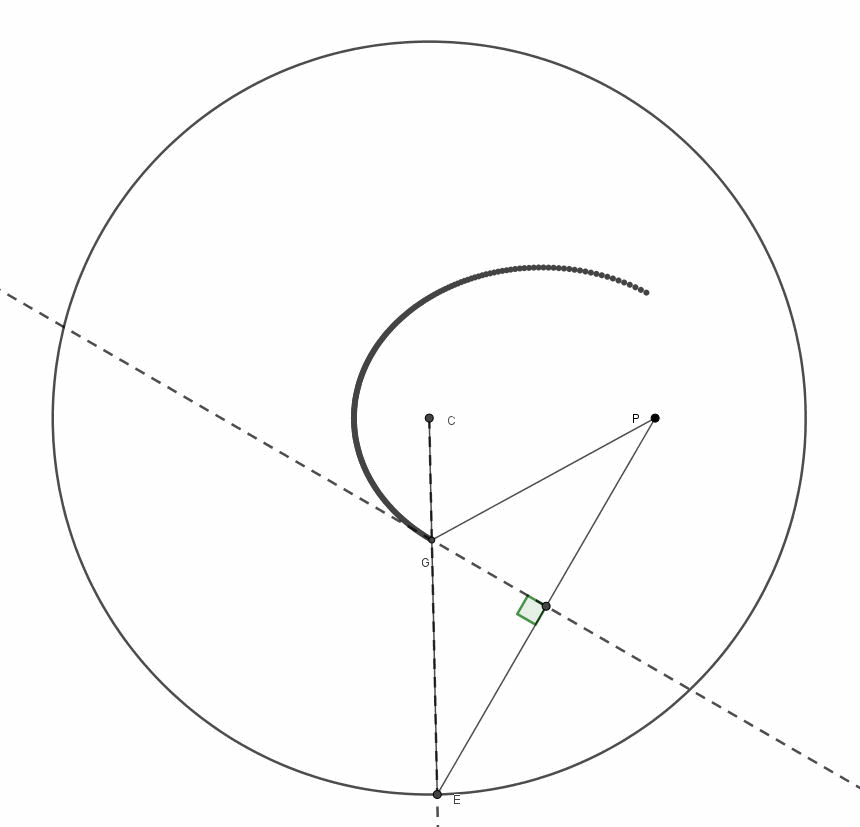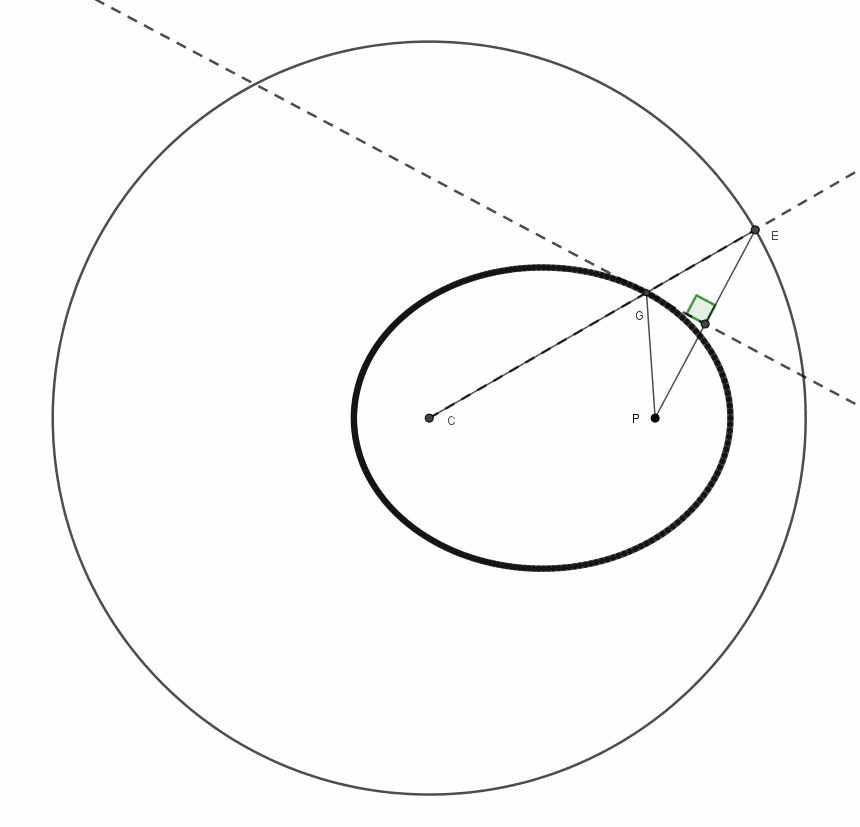
Figura 6

Il fatto più importante, però, è che ogni segmento ruotato di 90° risulta tangente a un punto dell’ellisse e, quindi, indica la direzione della velocità di un corpo che la descrive. Questa banale constatazione sarà utilissima alla fine della nostra “avventura”. Per i più pignoli possiamo facilmente confermare che il segmento ED è tangente alla ellisse nel punto Q, dato che qualsiasi altro punto del segmento (sia a destra che a sinistra di Q) darebbe luogo a una somma maggiore del raggio R del cerchio, ossia:

CD + DA > AC = R

AM + MC > AC = R

AB + BC > AC = R

Mettiamo questa costruzione nel cassetto della memoria, perchè la tireremo fuori al momento opportuno.

La seconda legge di Keplero

Prima di iniziare, ripeto i primi due principi di Newton utilizzando proprio le sue parole (tradotte):

1. Ciascun corpo persevera nel suo stato di quiete o di moto rettilineo uniforme, salvo che sia costretto a mutare quello stato da forze applicate ad esso.
2. Il cambiamento di moto è proporzionale alla forza motrice risultante applicata, ed avviene lungo la linea retta secondo la quale la forza stessa è stata esercitata. Questo moto, se il corpo era già mosso, viene aggiunto al moto di quello.

Bene, rinfrescata un po' la memoria, vediamo di determinare la seconda legge di Keplero senza alcuna equazione differenziale o calcolo complicato.

Sia O un corpo che si muove con velocità costante lungo una linea retta come indicato dal Primo Principio. Essendo la velocità costante, esso compirà tragitti uguali in tempi uguali, come mostrato in Fig. 7.

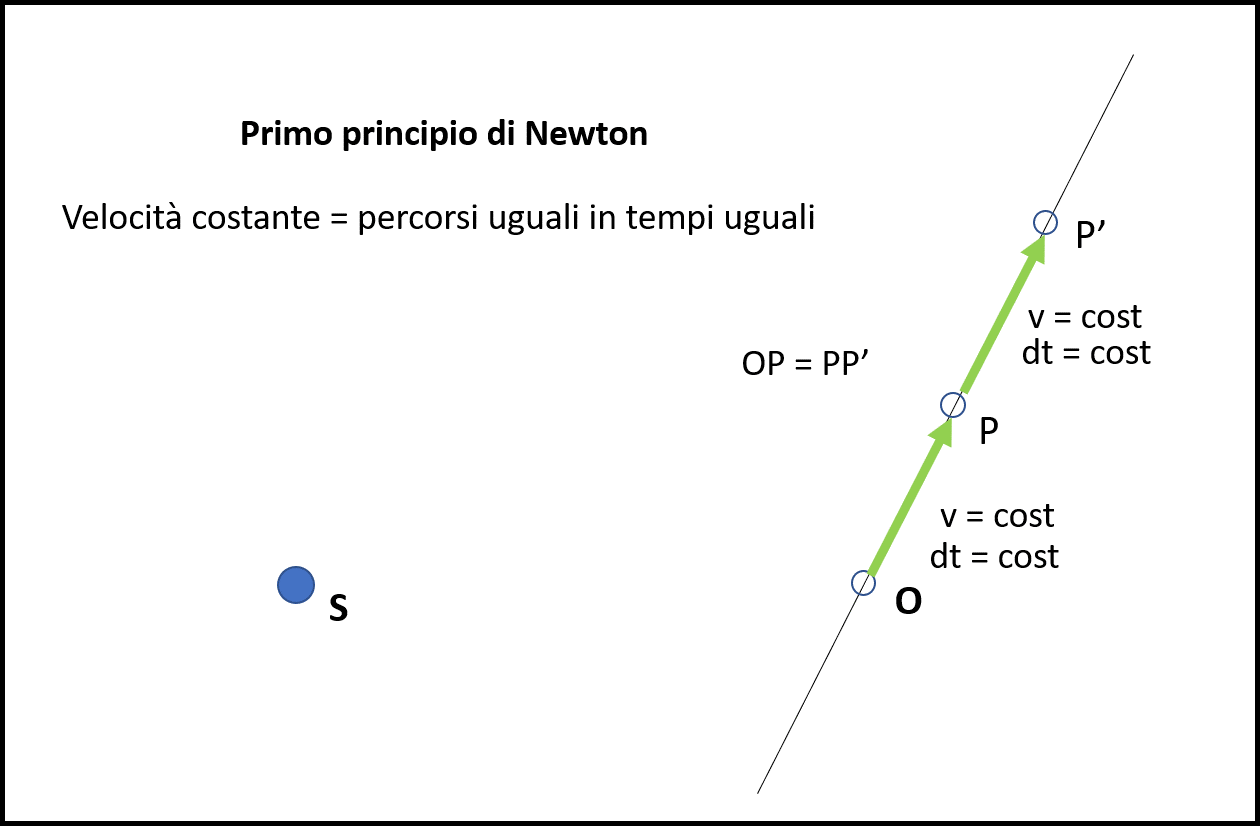
In un certo tempo dt il corpo O si porta in P e poi, sempre nello stesso tempo, si porta in P'. Essendo la velocità costante non abbiamo problemi a considerare tempi anche molto lunghi. In seguito, però, continueremo a usare triangoli di dimensioni considerevoli, pensando che il tempo trascorso sia molto piccolo così come  il tragitto percorso dal corpo celeste. La possibilità di ridurre a piacere le dimensioni di ogni tratto percorso ci garantisce che la correttezza delle conclusioni.

A sinistra del nostro corpo (che possiamo anche considerare un pianeta) si vede il Sole S, che immaginiamo, però, dormiente del tutto e incapace perfino di influenzare con la sua massa il moto del pianeta. Lo utilizziamo, per adesso, solo come origine dei segmenti che andiamo a tracciare. In poche parole, congiungiamo S con O, con P e con P'.  Otteniamo i due triangoli SOP e SPP' di Fig. 8.

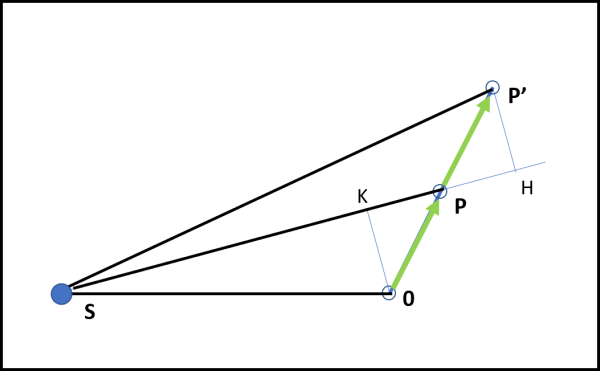
Ci vuole un attimo (Fig. a concludere che le loro aree sono uguali. Essi hanno la stessa base SP e la stessa altezza OK = P'H. Le due altezze sono uguali, in quanto cateti di due triangoli rettangoli uguali (PKO e P'HP), dato che hanno la stessa ipotenusa (tragitto compiuto dal pianeta nel tempo dt) e gli angoli in P uguali perché opposti al vertice. Ne segue che i due triangoli hanno la stessa area.

Lo stesso procedimento  può essere usato per i tratti P'P'' e P''P''' di Fig. 9.

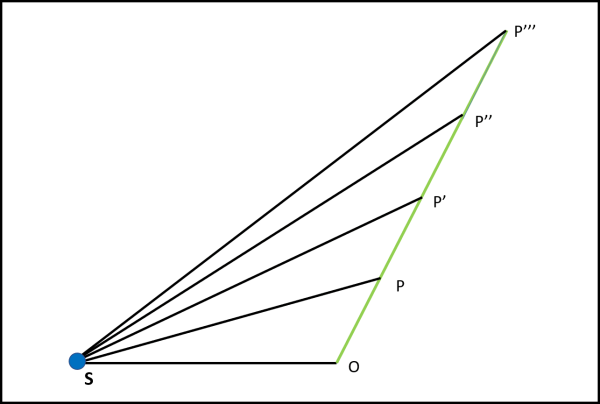
Il che ci permette di concludere che, rispetto a un punto fisso S, le aree spazzate dal pianeta in tempi uguali, durante il suo moto rettilineo uniforme, sono sempre uguali.

In qualche modo, abbiamo già dimostrato la seconda legge di Keplero che dice che le aree spazzate in tempi uguali dai pianeti attorno al Sole sono uguali. Beh... sarebbe vincere in modo troppo facile. L'esempio considerato finora considera un Sole del tutto ininfluente, anche se quanto trovato vale per qualsiasi posizione passata e futura del nostro pianeta che se ne va dritto per la sua strada. Parlando seriamente, possiamo concludere che, se il Sole non esercitasse alcuna forza, il solo primo principio della dinamica stabilirebbe che le aree spazzate dal pianeta (vagabondo) devono restare uguali.

Facciamo, allora entrare in gioco anche il secondo principio della dinamica. Il Sole si accende sotto tutti i punti di vista: non solo diventa rosso ma esercita una forza sul pianeta. Il secondo principio dice che tale forza implica uno spostamento del moto  nella direzione della forza agente che possiamo ipotizzare diretta verso il Sole.

F = ma = m dv/dt  = m ds /dt² ∝ ds           (il segno ∝ sta per "proporzionale a")

Tale forza deve dar luogo a un movimento diretto in quella direzione che deve essere sommato a quello preesistente, come mostrato in Fig. 10.

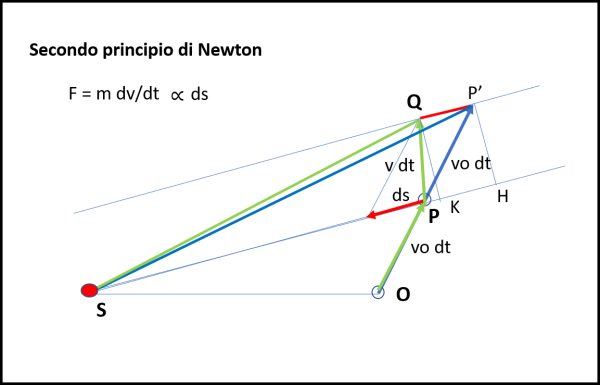
Lasciamo perciò tranquillo il nostro pianeta tra O e P, ma poi, in P applichiamogli la forza F diretta verso il Sole che da luogo a uno spostamento ds verso di lui, che si deve sommare a quello vo·dt che il corpo aveva nel suo moto rettilineo uniforme. In conclusione, dopo un intervallo di tempo dt (sempre lo stesso), il pianeta si è spostato di v·dt, ossia percorre  il segmento PQ. Non ci resta, adesso, che dimostrare che anche il triangolo SQP ha la stessa area del triangolo SP'P (a sua volta uguale, come appena dimostrato, a quella di SPO).

Si vede subito che i due triangoli hanno la stessa base SP, ma anche la stessa altezza QH = P'K, dato che QP' è parallela a SP per costruzione.

Facciamo molta attenzione a un fatto decisamente importante, illustrato in Fig. 11

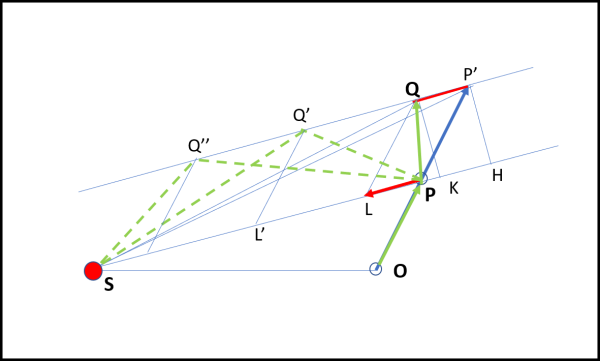
Dato che QP' è parallela a SP, possiamo considerare qualsiasi  deviazione PL, PL', PL''..., dovuta alla forza esercitata dal Sole. L'unica cosa che cambierebbe sarebbe il punto Q, che diventerebbe Q' , Q'', ecc. Ma i triangoli SQ'P, SQ''P, ... avrebbero sempre la stessa area di QSP. L'area spazzata dal pianeta sotto l'azione di una forza diretta verso il Sole, qualsiasi sia la sua intensità, resta sempre uguale, lavorando su intervalli di tempo uguali. O, se preferite: la forza che attrae il pianeta verso il Sole cambia la traiettoria, ma non il valore dell'area spazzata.

La costruzione fatta in Fig. 10 può essere applicata nuovamente al tratto successivo, come mostra la Fig. 12:

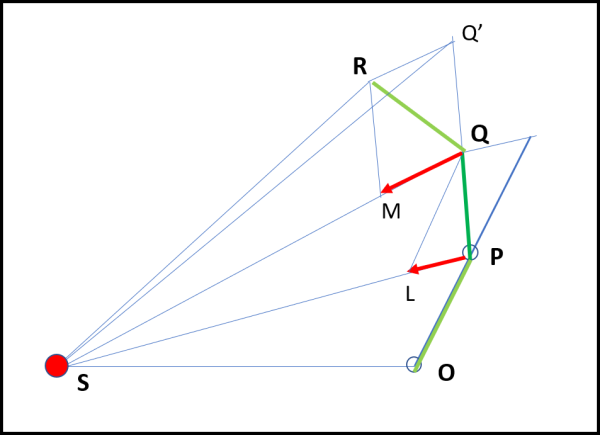
Il pianeta proseguirebbe verso Q', ma il Sole impone lo spostamento QM. Il segmento RQ' è parallelo a MQ e, come nel passo precedente, i triangoli SRQ e SQQ' hanno la stessa area. Ma SQQ' ha la stessa area di SPQ, dato che QQ' è uguale a PQ (la velocità resta costante se non ci fosse la forza del Sole). La faccenda si ripete pari pari ogni volta, assumendo sempre lo stesso intervallo di tempo dt. Come già accennato possiamo scegliere MQ di lunghezza qualsiasi.

Continuando in questo modo si può costruire l'intera traiettoria del pianeta attorno al Sole e si dimostra facilmente che tutte le aree spazzate in tempi uguali sono uguali, ossia vale la seconda legge di Keplero.

N.B.: segue un inserto un po' più difficile, ma molto utile

Si può anche dimostrare facilmente che questa conclusione equivale a dire che il momento angolare deve rimanere costante.

Usiamo la Fig. 13

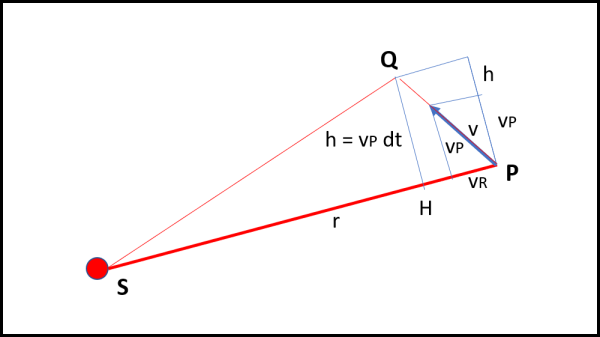
Il tragitto compiuto dal pianeta durante il tempo dt non è altro che v dt. Tuttavia v possiamo spezzarla in due componenti : v_P e v_R, la prima perpendicolare alla distanza r tra S e P,  la seconda  lungo la direzione SP. L'altezza  h è allora uguale a v_P dt.

Quanto vale l'area del triangolo "spazzata" dal pianeta?

A = 1/2 r h = 1/2 r v_P dt = costante              (come dimostrato precedentemente).

Quanto vale il momento angolare I ?

I = mv ∧ r

Siamo di fronte a un prodotto vettoriale e il risultato è un vettore. Possiamo, però, dividere la quantità di moto mv nelle sue due componenti:

mv = mv_P + mv_R

Vale ancora:

I = mv ∧ r = mv_P ∧ r + mv_R ∧ r

Ricordiamo che il momento angolare di un vettore diretto verso il centro S è nullo (c'è di messo un seno),  Quindi resta soltanto:

I = m v_P ∧ r

il cui modulo è

I = m v_P r                                      .... (1)    (il seno dell'angolo è uguale a 1)

Ma dalla (1) abbiamo che 

v_P r = 2A/dt

Sostituiamolo nella (1) e otteniamo:

I = m 2A/dt = costante.

Abbiamo dimostrato in modo banalissimo che la frase "spazzare aree uguali in tempi uguali" equivale perfettamente a dire che  "il momento angolare del pianeta durante il suo moto attorno al Sole rimane costante". Grande Feynman!!

Fine inserto "difficile" (non certo per chi conosce il momento angolare...)

Torniamo a noi e ai nostri triangoli.

Abbiamo dimostrato la seconda legge di Keplero utilizzando solo i primi due principi della dinamica, ma non possiamo certo essere soddisfatti. Infatti, la legge vale qualsiasi sia l'intensità della deviazione imposta dalla forza diretta verso il Sole. In altre parole, cambiandola a piacere, potremmo ottenere qualsiasi percorso, anche il più bizzarro e caotico.

Senza esagerare con forze ballerine, potremmo decidere che la forza rimanga costante qualsiasi sia la distanza del pianeta . Non è difficile costruire la traiettoria che ne segue e che non si chiude mai, come mostrato nella sua costruzione riportata in Fig. 14 (da sinistra verso destra).

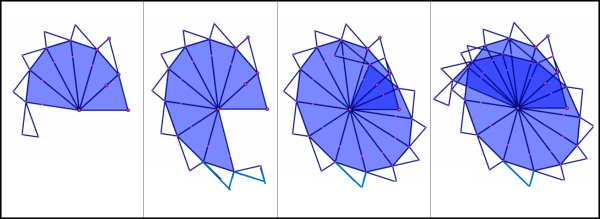
Insomma, per potere decidere qual è la vera traiettoria non basta aver trovato la seconda legge di Keplero. Bisogna dare la definizione della forza che agisce sul pianeta. In altre parole, bisogna accettarla o ricavarla utilizzando la terza legge di Keplero.

La terza legge di Keplero

Pur avendo ricavato la seconda legge di Keplero, ben poco si può dire sulla  traiettoria di un pianeta attorno al Sole. Per fare questo passo in avanti è necessario conoscere come agisce la forza esercitata dal Sole, in funzione della distanza del pianeta.

Sicuramente la forza deve essere valida per tutte le orbite fisicamente possibili.  Scegliamone, allora una molto particolare che sia oltremodo realistica, anche se decisamente semplice.

Cominciamo a costruire la nostra traiettoria con il metodo usato finora, ma imponendo che le velocità passo dopo passo rimangano sempre costanti. L'unico modo per riuscirci è far rimanere costante anche la distanza dal Sole. La Fig.  15  (a sinistra) ci illustra la costruzione eseguita.

Figura 15

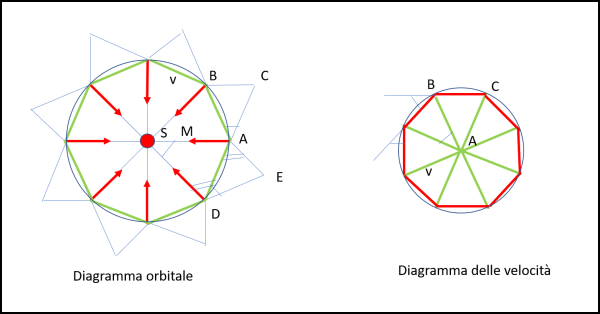
Beh... una traiettoria ben nota che aumentando il numero di lati ci porta a una circonferenza di raggio uguale alla distanza costante tra Sole e pianeta. D'altra parte, la nostra traiettoria poligonale ha tutti lati uguali per costruzione. Inoltre, l'angolo SDA è uguale all'angolo DAE (alterni interni di rette parallele per costruzione) e quindi, essendo i triangoli DAE, BAC, ... tutti uguali e isosceli (nuovamente per costruzione) anche l'angolo supplementare di BAC deve rimanere sempre lo stesso per ogni angolo del poligono (tra parentesi questo angolo è anche uguale a quello al centro). Insomma, il poligono che abbiamo costruito ha i lati tutti uguali e anche gli angoli ai vertici, ossia ha i giusti requisiti per essere dichiarato un poligono regolare.

Sì, lo so... si vedeva subito che era un poligono regolare, essendo costruito con otto triangoli isosceli, ma ho voluto usare la via più lunga per definire esattamente un poligono regolare, dato che ci servirà in seguito.

Assodata la traiettoria "regolare", possiamo costruire (Fig. 15, a destra) un altro poligono estremamente importante: a partire dal punto A tracciamo tutte e otto le velocità del primo diagramma ( AC è uguale a DA),  e via dicendo... Cosa sono i lati del nuovo ottagono? Ovviamente le differenza tra le velocità, ossia proprio gli spostamento del pianeta verso il Sole ad ogni passo (AM diventa il lato BC). In altre parole, il poligono delle velocità viene costruito con i triangoli azzurri costruiti sui lati del poligono delle distanza dal Sole (quello a sinistra). Anche questo è sicuramente un poligono regolare avendo i lati tutti uguali (le variazioni delle velocità sono uguali  per costruzione) e tutti gli angoli supplementari a quelli tra i lati stessi anch'essi uguali dato che sono sempre diretti verso il Sole e sappiamo che l'angolo tra loro rimane costante (è sempre l'angolo al centro dei triangoli isosceli del poligono delle distanze).

Cosa succede, allora, facendo muovere il pianeta a velocità costante lungo la traiettoria di sinistra? Dopo 360° di rotazione si torna al punto di partenza (siamo di fronte a un moto circolare uniforme). Ma la stessa cosa capita anche per la "punta" delle velocità del diagramma di destra che descrive anch'essa una traiettoria che si completa dopo 360°.

E' ora di scrivere qualche semplice formula che descriva sinteticamente e numericamente quanto abbiamo detto a parole.

Possiamo tranquillamente considerare i due diagrammi delle circonferenze (basta aumentare il numero di triangoli isosceli di partenza).

Per il primo a sinistra la variazione dello spazio in un certo tempo dt vale:

v = ds/dt = 2π R/P        .... (2)      (dove R è la distanza costante Sole - pianeta e P è il periodo orbitale)

Per il secondo a destra  la variazione di velocità in un certo tempo dt vale:

dv/dt = 2π v/P               .... (3)              (dove v è la velocità costante del pianeta e P è lo stesso di prima)

Abbiamo solo scritto che ogni volta che il pianeta compie un'orbita, la sua velocità compie anch'essa una rotazione di 360° nel diagramma delle velocità.

Tuttavia sappiamo che la forza impartita dal Sole vale , utilizzando la (2)  e la (3)

F = mdv/dt ∝ dv/dt = 2π v/P = 2π(2π R)/P²  ∝ R/P²              .... (4)

Ma la terza legge di Keplero (dato osservativo!) ci dice che:

P² ∝ R³              .... (5)

Inserendo la (5 ) nella (4)   otteniamo:

F ∝ R/P2 ∝ R/R³ = 1/R²

Ossia, si dimostra che la forza esercitata dal Sole è proporzionale all'inverso del quadrato della distanza del pianeta. Noi l'abbiamo ricavata da un caso particolare, ma la forza è quella che è e non cambia certo cambiando la traiettoria. Ne segue che questa legge è applicabile a tutte le traiettorie per cui vale la seconda legge di Keplero.

La terza legge di Keplero conoscendo la  forza

A noi, però, interessa soprattutto fare il contrario, ossia conoscere la forza e ricavare la terza legge di Keplero, E' un gioco veramente banale, ma estremamente importante, dato che risolve un punto normalmente raggiungibile con equazioni differenziali. La formula da utilizzare è sempre la (4)

F = mdv/dt ∝ dv/dt = 2π v/P = 2π(2π R)/P²  ∝ R/P²   

Ma desso ciò che sappiamo è che la forza è proporzionale all'inverso del quadrato della distanza, ossia:

F  ∝ 1/R²

Ne segue che possiamo scrivere:

 1/R² ∝ R/P²   

Ossia:

P²  ∝ R³

che è proprio la terza legge di Keplero

Generalizziamo allora il problema, come riportato in Fig. 16, utilizzando molti triangoli per costruire la poligonale, conoscendo, però, la legge della forza che abbiamo ricavata dal caso particolare precedente.

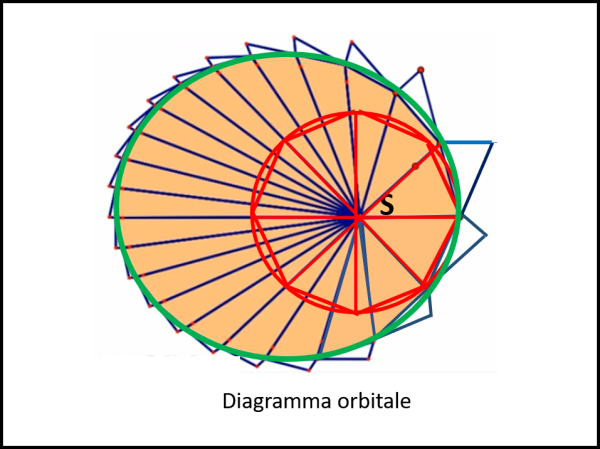
Come si vede bene, è facile a questo punto costruire la curva continua che rappresenta l'orbita del pianeta. Per confronto è stato inserita in rosso anche la traiettoria del caso precedente.

Abbiamo risolto qualcosa. Beh... in realtà non molto, dato che la curva è molto bella ma non sappiamo assolutamente che cosa rappresenta!

Dobbiamo rispondere ancora a due domande:

1. La curva delle velocità costruita sulla base delle velocità calcolabili dalla poligonale è un poligono regolare, come nel caso dell'orbita circolare?
2. E se per caso lo fosse, come potrebbe dirci che curva la è un'ellisse?

Cominciamo con la prima domanda. E' facile costruire il diagramma delle velocità, in modo analogo a quanto fatto per quello di Fig. 15. Attenzione, però... la figura si basa sulla seconda legge di Keplero, ossia aree uguali in tempi uguali e ne segue che le velocità cambiano da punto a punto. Sì, è vero che possiamo tracciarne quante ne vogliamo, ma il diagramma che otteniamo alla fine, e che ha come lati le variazioni di velocità, non ha assolutamente le caratteristiche di un poligono regolare: i lati sono tutti diversi. Basta disegnare la poligonale delle distanze dal Sole e la relativa poligonale delle velocità per rendersene conto (Fig. 17).

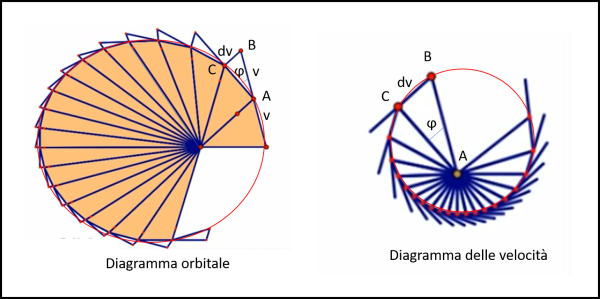
I segmenti relativi alle velocità sono proporzionali ai lati del poligono di sinistra, in quanto la lunghezza dei lati è proporzionale alla velocità, essendo dt una costante (aree uguali in tempi uguali). Potremmo, comunque, considerare anche dt come valore unitario e usare il lato del poligono come valore della velocità.

In parole matematiche:

v = ds/dt        con dt costante.

Se dt = 1

v = ds

Notiamo, in particolare, che il triangolo ABC  di sinistra si trasferisce pari pari nello stesso triangolo ABC di destra. Essi sono  comunque simili  (due lati proporzionali e l'angolo compreso φ uguale per costruzione) e scalano a seconda del dt considerato e quindi dell'area spazzata. Come detto, se considerassimo dt = 1, i triangoli di sinistra sarebbero uguali a quelli destra. Nelle figure abbiamo mantenuto il parallelismo tra i segmenti della figura di sinistra e quelli della figura di destra.

Ribadiamo, ancora una volta, che le aree spazzate sono proporzionali all'intervallo di tempo dt considerato. Tempi uguali vogliono infatti dire aree uguali.

dt ∝ A

dove A è l'area spazzata.

Sì, sì... tante belle parole, ma il poligono di destra continua a non essere un poligono regolare!

Dobbiamo proprio affidarci al genio ELEMENTARE di Feynman.

Il diagramma delle velocità

Abbiamo costruito il diagramma delle velocità corrispondente a una traiettoria che segua la seconda legge di Keplero e in cui la forza di attrazione vada con l'inverso della distanza al quadrato. Tuttavia, non  sappiamo ancora che traiettoria sia e, soprattutto, non abbiamo ancora dimostrato che il diagramma delle velocità sia proprio un poligono regolare. Iniziamo con quest'ultimo problema.

Ribadiamo le condizioni necessarie per avere un poligono regolare: tutti i lati devono avere uguale lunghezza e tutti gli angoli dei vari spigoli devono avere la stessa ampiezza. Noi, invece, abbiamo un bel poligono che si chiude, ma è stato costruito sulla base delle distanze (velocità) sempre diverse, fatte partire da un punto che, comunque, non potrà mai essere il centro del cerchio circoscritto al poligono (sempre che esista). Riprendiamo la poligonale costruita la volta scorsa (Fig. 18).

I vari lati sono proporzionali a dv. Tuttavia, questi valori cambiano continuamente, in quanto la costruzione si è basata su triangoli tali da avere sempre la stessa area a parità di tempo trascorso (seconda legge di Keplero).

Cambiamo, allora, la procedura e consideriamo triangoli che abbiano lo stesso angolo al Sole  θ. Si ottiene, per la traiettoria del pianeta, una poligonale come quella di Fig. 19.

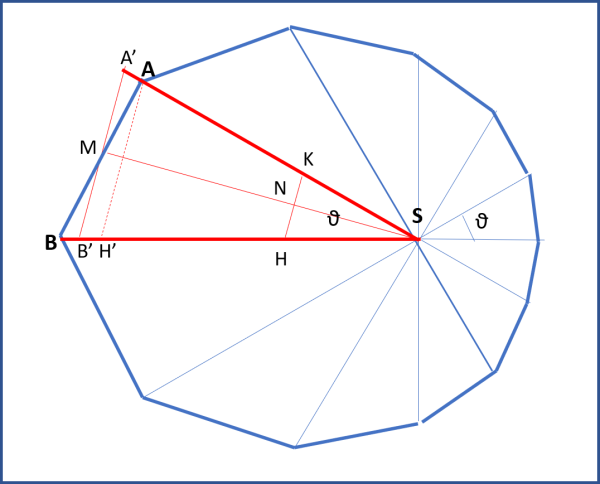
Ovviamente, le aree non sono più uguali e quindi tale non è nemmeno il tempo impiegato a spazzarle, dato che sappiamo che vale:

Area ∝ dt

Ossia più l'area è grande e più tempo impiegherà il pianeta a spazzare il triangolo.

Occupiamoci, allora, del triangolo ABS (ma il discorso vale per tutti). Esso tutto è fuorché isoscele, tuttavia possiamo tracciare un segmento  HK perpendicolare alla bisettrice dell'angolo θ (ASB). Facciamo  scorrere questo segmento (allungandolo gradatamente) fino a farlo arrivare in AH'. Poi, proseguiamo fino a che l'area del triangolino AA'M non sia uguale all'area del triangolo MBB'.  Per costruzione A'B' è perpendicolare a SM e il triangolo A'B'S è isoscele. Ne segue che l'area del triangolo ABS è uguale a quella del triangolo isoscele A'B'S, di cui SM è l'altezza.

Calcoliamo l'area del triangolo  A'B'S = ABS

A_ABS = 1/2 A'B'· SM                  .... (6)

Il triangolo A'B'S' è simile al triangolo HKS, per cui possiamo scrivere:

KH: A’B’ = SN: SM

A'B' = SM·KH/SN

Sostituendo nella (6) abbiamo:

A_ABS = (1/2KH/SN)SM²  ∝ SM² = R²            .... (7)

In altre parole, l'area spazzata è proporzionale al quadrato della distanza dal Sole  R = SM.

Ed eccoci al piccolo grande capolavoro di Feynman...

Noi sappiamo che per la forza diretta verso il Sole vale:

F = ma  ∝  a = dv/dt ∝ 1/R²

ossia:

dt ∝ dv R²           .... (8)

ma sappiamo anche che:

A_ABS  ∝ dt

e, quindi, dalla (7), che:

dt ∝ R²

Sostituendo dt nella (8), otteniamo:

R² ∝ dv R²

ossia:

dv ∝ 1

In parole più semplici dv è una COSTANTE. E questo vale per qualsiasi punto della traiettoria per come l'abbiamo costruita. L'importante è che i triangoli abbiano sempre lo stesso angolo al Sole  θ. Ovviamente, più l'angolo è piccolo e più diminuiscono le aree dei triangoli e sempre più la poligonale si avvicina a una curva.

Si può allora ottenere il diagramma delle velocità sostituendo ai triangoli di area uguale, triangoli con lo stesso angolo al Sole. Questa volta, però, il poligono che ne consegue ha tutti lati (dv) uguali tra di loro, così come gli angoli supplementari a quelli degli spigoli in quanto dv è sempre diretto verso il Sole e quindi l'angolo tra di loro deve essere uguale a θ . Ecco il nuovo diagramma delle velocità mostrato a destra in Fig. 20.

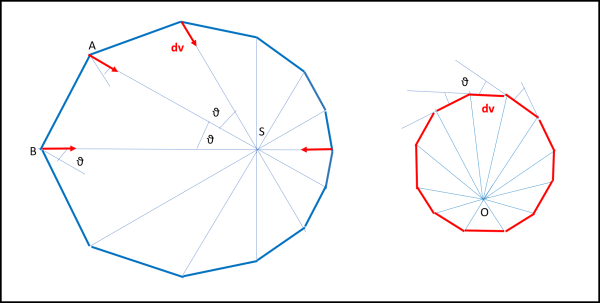
Il concetto è molto chiaro e Feynman è riuscito a costruire, finalmente, un diagramma delle velocità che sia un poligono regolare e che quindi possa portare (aumentando sempre più i lati e rimpicciolendo i triangoli) a un cerchio perfetto. E' però interessante vedere come costruire in pratica questo diagramma... io presento due metodi, di cui uno del tutto personale, ma che in pratica dicono la stessa cosa... Utilizziamo la Fig. 21.

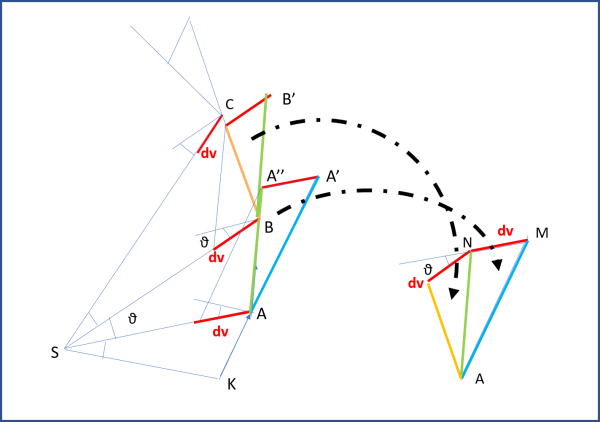
Attenzione: Le velocità sono sempre dirette lungo i lati del poligono delle posizioni (a sinistra), continuando a cambiare da vertice a vertice, dato che cambia sia il dt relativo a ciascuna area, sia lo spazio percorso (il lato).  Ciò che non cambia mai è il dv, ossia la differenza tra le velocità di ogni singolo lato del poligono. Essa è stata dimostrata essere una costante.

Allora, basta prendere un segmento parallelo a KA e uno parallelo ad AB (poligonale di sinistra, quella delle posizioni), Farli partire dallo stesso punto A, che rimarrà sempre il punto di origine, prolungare KA fino ad  AA' e AB fino ad AA" in modo che A'A" uguagli dv (in modulo, e direzione) che deve rimanere costante. In  tal modo abbiamo costruito il triangolo AMN del diagramma delle velocità che è uguale a quello AA'A" del diagramma orbitale. Poi passiamo al punto B del diagramma di sinistra e tracciamo le due direzioni delle velocità (quella che arriva in B e che è la velocità gialla e quella che parte da B, verde, e che è deviata a causa dell'attrazione solare) fino a formare di nuovo una differenza tra le due che sia proprio dv. Si ottiene il triangolo BCB' che può essere spostato nel digramma delle velocità, sicuri che AN coincida con BB' (E' la stessa velocità di arrivo e di partenza da B). E via dicendo fino a completare il diagramma di destra che è proprio quello delle velocità.

Oppure, come fa Feynman, partire direttamente dal diagramma delle velocità (Fig. 22), disegnando un segmento pari a dv e parallelo a quello del diagramma delle posizioni (a destra).

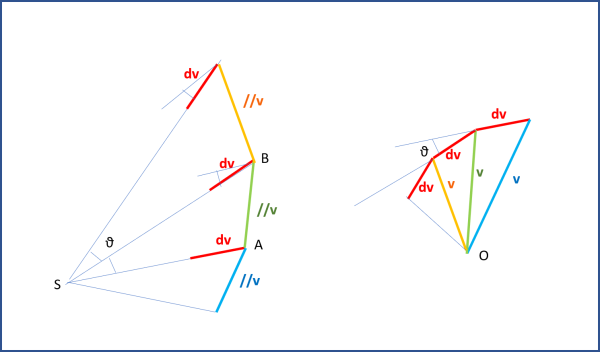
Dai suoi estremi tracciare le parallele alle due velocità (blu e verde) relative al punto A del diagramma orbitale (a destra). Le due parallele si incontrano in un punto O. Di seguito al primo dv inserisco il secondo dv parallelo a quello ricavato dal diagramma di destra. Dal suo estremo di sinistra traccio la parallela alla velocità gialla di B. E via dicendo... Nuovamente siamo sicuri che tutte le dv sono uguali (per costruzione) e anche gli angoli del poligono delle velocità dato che tra le dv l'angolo è sempre lo stesso.

Scegliete voi il metodo che preferite e costruitevi l'intero diagramma delle velocità.

Attenzione, però... non vi venga in mente di dire che l'angolo θ è uguale all'angolo in O del diagramma! L'angolo θ è qualcosa di differente (fortunatamente!).

Ricapitoliamo, disegnando la poligonale delle velocità completa in Fig. 23.

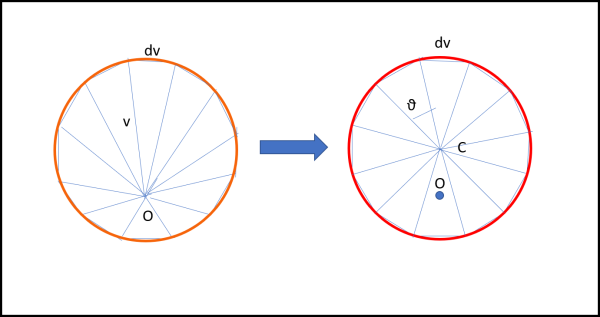
Sappiamo ormai -e lo abbiamo dimostrato- che il poligono è regolare e che può essere ricondotto a un cerchio di cui O non è assolutamente il centro. Disegniamo, invece, il centro C del cerchio che ormai siamo sicuri che esista e congiungiamolo con tutti i punti del poligono. Nel caso della Fig. 23 questi punti sono 12 tanti come quelli che ci sono serviti per costruire il diagramma delle posizioni (orbitale). Otteniamo, per costruzione,  12 triangoli isosceli tutti uguali. L'angolo al centro è quindi 360°/12. Ma anche i triangoli dell'orbita sono 12 a hanno lo stesso angolo al Sole θ per costruzione. 12 di questi angoli fanno un angolo giro e quindi  devono essere uguali e  360°/12 ciascuno. In poche e banali parole: l'angolo θ è uguale all'angolo al centro del poligono delle velocità.

Qualsiasi orbita che segua la seconda legge di Keplero e la forza di gravità (che deriva dalla terza legge) deve portare a un diagramma delle velocità che sia un poligono regolare e quindi, per θ tendente a zero, riducibile a una circonferenza.

Bene... non ci resta che fare l'ultimo passo. Abbiamo a disposizione la circonferenza delle velocità e vogliamo dimostrare che ciò implica che la traiettoria che ci è servita per costruirla è proprio un'ellisse.

Costruiamo l'ellisse

Chi si ricorda l'introduzione si sarà già accorto che il diagramma delle velocità assomiglia in tutto e per tutto al cerchio iniziale. Basterebbe applicare a lui il procedimento usato allora e salterebbe fuori l'ellisse.

Tuttavia, arriviamo alla soluzione con la massima calma e attenzione.

In Fig. 24, disegniamo a sinistra il diagramma delle velocità e a destra la traiettoria del movimento di un pianeta che segua la seconda legge di Keplero e che subisca una forza di attrazione da parte del Sole diretta nella sua direzione e che vada con l'inverso del quadrato della distanza (legge che abbiamo determinato attraverso la terza legge di Keplero).

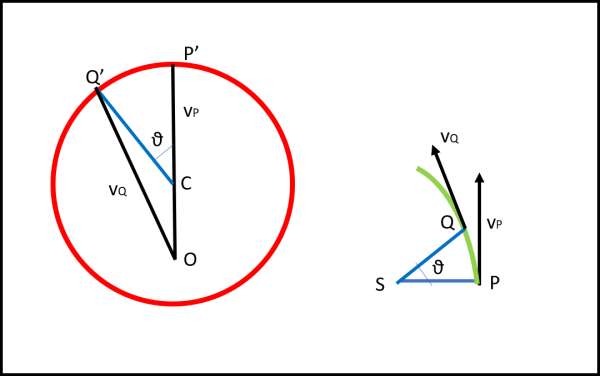
Abbiamo anche dimostrato che l'angolo al centro θ tra gli estremi delle velocità di P e di Q (P' e Q')  è uguale all'angolo al Sole tra i due punti P e Q. Ricordiamo anche che le linee da O (punto eccentrico che ci ha permesso di costruire il cerchio delle velocità) ai punti della circonferenza sono proprio le velocità dei vari punti della traiettoria. In altre parole, facendo variare il punto sul cerchio delle velocità, i segmenti OP', OQ' ecc. descrivono le tangenti (direzione delle velocità) dei punti P e Q sul diagramma orbitale. Un giro completo del punto sulla circonferenza del diagramma delle velocità equivale a un'orbita completa.

Praticamente, dobbiamo dimostrare che la traiettoria che ha come tangente in ogni suo punto la velocità del diagramma delle velocità è proprio un'ellisse.

Per ottenere il risultato voluto, Feynman fa un'operazione banalissima, ma geniale: ruota il diagramma-cerchio delle velocità di 90 ° verso destra in modo che i lati dell’angolo θ risultino paralleli tra un diagramma e l’altro. La linea indicata con “v_P”, che era parallela alla velocità in P, ora è perpendicolare (Fig. 25).

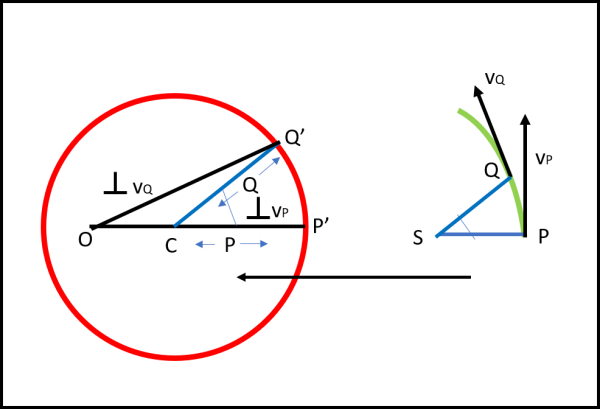
Il punto P, per il quale la velocità è massima, deve stare su  SP , parallelo a CP', e deve avere una velocità che è data dalla perpendicolare alla velocità relativa a P' nel cerchio delle velocità, dato che è stato ruotato di 90°.Analogamente il punto Q deve stare sulla parallela a CQ', passante per il Sole (l'angolo θ è lo stesso) e deve avere come tangente la perpendicolare alla velocità ruotata OQ'. Possiamo tranquillamente traslare il diagramma di destra fino a fare coincidere S con C. Non possiamo, però, sapere le distanze CP e CQ.

Tuttavia, questo non è un problema, in quanto è comunque possibile costruire l'orbita che segue le due proprietà appena richiamate, del tutto sufficienti a disegnare una traiettoria che sia come forma e direzione simile a quella reale. Conoscendo la distanza dal Sole di un solo punto dell'orbita reale sarà poi possibile scalare la nostra curva fino a farla passare per quel punto. In tal modo la traiettoria sarà sicuramente quella percorsa dal pianeta che segue le proprietà riassunte nella costruzione del cerchio delle velocità.

A questo punto possiamo ripetere pari pari la costruzione dell'Introduzione, lavorando direttamente nel diagramma delle velocità (Fig. 26).

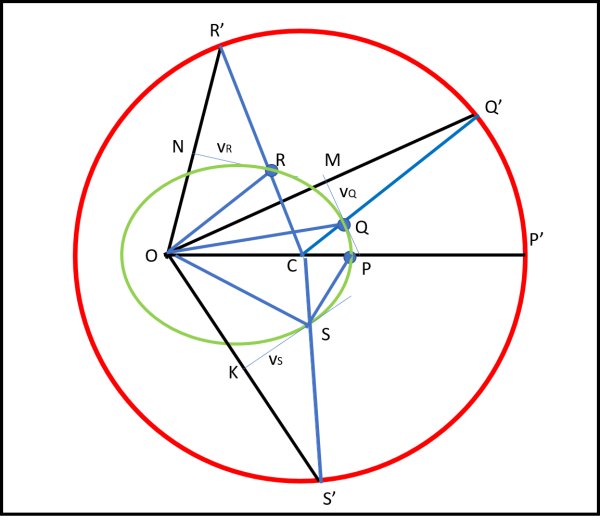
Uniamo il centro O con un punto qualsiasi della circonferenza, ad esempio Q'. Dal punto di mezzo M del segmento OQ' tracciamo la perpendicolare, parallela alla velocità del corrispondente punto Q dell'orbita (per costruzione, dato che abbiamo ruotato di 90° il diagramma). Uniamo C con Q'. Il punto intersezione tra CQ' e la perpendicolare  tracciata prima deve essere un punto dell'orbita, in quanto ha la giusta tangente e il giusto angolo al Sole QCP (θ).

Resta solo da verificare se è un'ellisse... Calcoliamo la somma delle due distanze di Q dal punto O e dal punto C e controlliamo che essa dia sempre lo stesso risultato al variare di Q. Costruiamo il punto R con la stessa procedura e otteniamo i segmenti RC e RO.  Sommiamoli assieme e confrontiamoli con la somma precedente. Prima, però, dobbiamo accertare che i triangoli rettangoli QMO e MQQ' siano uguali. Lo sono senz'altro avendo due lati uguali (OM e MQ') per costruzione e MQ in comune. Ne segue che QQ' = QO e, analogamente, RR' = OR. Possiamo, allora scrivere:

CQ + OQ = CQ + QQ' = raggio del cerchio delle velocità

RC + OR = RC + RR' = raggio del cerchio delle velocità.

La curva descritta da un pianeta attorno al Sole deve, perciò, essere un'ellisse, con i fuochi in O e in C.

Prima di terminare, notiamo un fatto importante legato all'ellisse ed estremamente importante per tutta la QED di Feynman, dato che si collega direttamente alla distanza minima percorsa dalla luce, ossia al principio di Fermat che dice: " ...di tutti i possibili cammini che un raggio di luce può percorrere per andare da un punto a un altro, esso segue il cammino che richiede il tempo più breve". Questo principio ha come conseguenza il cammino di un raggio di luce riflesso da uno specchio che trova il suo cammino più breve quando l'angolo di incidenza è uguale all'angolo di riflessione.

Consideriamo la Fig. 27, dove è riportata la nostra ellisse appena costruita (abbiamo già scritto F e F' al posto di O e C).

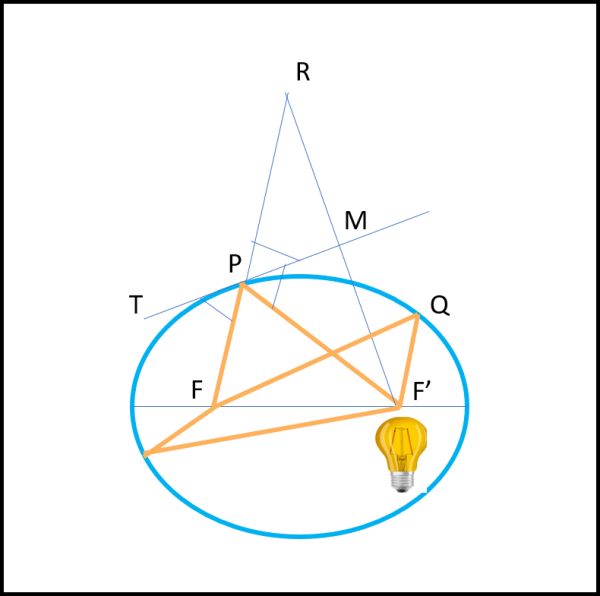
Manteniamo anche la costruzione del punto P e mettiamo una lampadina in F'. Rivestiamo di materiale riflettente l'interno della nostra ellisse. Vediamo cosa ci combina la traiettoria F'PF. Essa colpisce l'ellisse  in P, la cui tangente è proprio TM. Sappiamo che RPM = MPF'  (l'abbiamo appena dimostrato), ma dobbiamo concludere che anche TPF = RPM (angoli opposti al vertice). Ne segue che TPF = MPF'. Ma, allora, il raggio di luce FPF' si riflette sulla ellisse in modo che l'angolo di incidenza sia uguale a quello di riflessione. In altre parole è il percorso minimo della luce per andare da F a F'. Lo stesso, capita, però, anche per qualsiasi altro punto dell'ellisse, che risulta quindi il luogo dei punti di riflessione della luce che parte da F' e viene raccolta in F (e viceversa). Un altro fantastico modo "fisico" per definire un'ellisse.