Continuiamo a scoprire le magie di Mamikon e del suo metodo di calcolo visuale. Poi saremo pronti ad affrontare il problema della talpa aliena senza bisogno di nessuna formula che non sia quella del volume di una sfera...

Prima di iniziare (anzi... continuare) diamo una versione ancora più generale del teorema di Mamikon. A prima vista sembrerebbe meno importante, ma in certi calcoli è sicuramente più che utile:

L'area spazzata da un segmento di lunghezza variabile, tangente  a una curva qualsiasi,  è uguale all'area dell'insieme di tutti segmenti tangenti.

Per comprendere bene il suo significato basta guardare la Fig. 7. A sinistra una curva qualsiasi con segmenti tangenti di lunghezza variabile e a destra l'insieme di tutti i segmenti che abbiano in comune il punto di tangenza. Le due aree colorate sono sempre uguali.

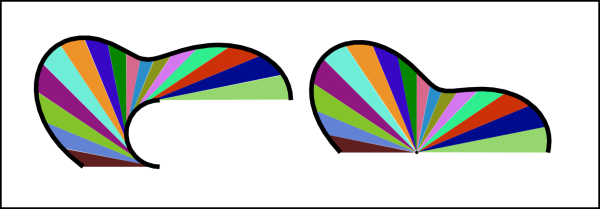
Come già detto, non vogliamo certo affrontare tutte le ricadute del calcolo visuale e quindi torniamo, ancora una volta, alla tangente di lunghezza costante. Questa volta, però, consideriamo una curva molto particolare: la trattrice.

In nome stesso la dice lunga: è una curva che indica il trascinamento e possiamo fare un esempio decisamente terra-terra, ma molto efficace. Una bambina sta trascinando dietro di sé un trenino per mezzo di un filo rigido e, quindi, di lunghezza costante d. Vediamo in Fig. 8 il caso di una bambina che cammini in linea retta (asse x)  e che cominci quando il trenino è posto in direzione dell'asse y.

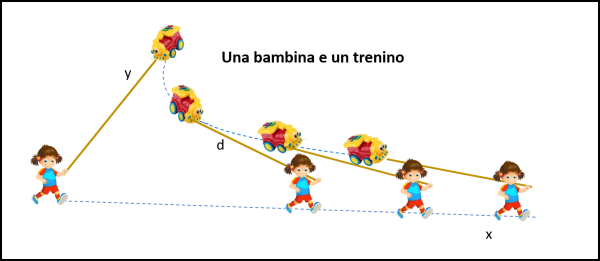
La curva ha una caratteristica molto interessante per noi: durante il movimento della bimba (con velocità costante e infinitesimale) non solo la lunghezza d si mantiene costante, ma il segmento si mantiene tangente alla curva istante per istante. Rappresentiamo la figura precedente in modo più ... rigoroso in Fig. 9.

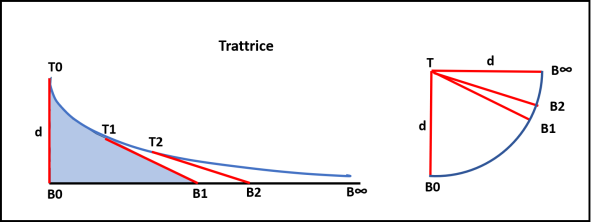
Non ci resta che applicare il teorema di Manikom, facendo coincidere i punti di tangenza nel punto punto T e tracciando tutte le distanze d parallele ai vari segmenti. Otteniamo un settore di cerchio di raggio d  con un angolo al centro uguale a 90°. L'area tra la trattrice e l'asse x non è altro che l'area del settore circolare, ossia:

A_TR = πd²/4

L'equazione della trattrice non è proprio banale e l'integrale corrispondente non banalissimo. Mamikon, però, ha avuto solo bisogno di conoscere l'area di un cerchio. Notiamo anche che si arriva all'infinito senza problemi (l'asse x è l'asintoto orizzontale della curva).

Passiamo ora a una curva molto più conosciuta, l'esponenziale in base e. Sappiamo che questa curva ha una caratteristica estremamente utile: la sua derivata è uguale alla funzione. Al limite il loro rapporto può essere uguale a una costante. E' meglio fare un esempio...

y = e^x             y' = e^x

y = e^bx           y' = be^bx

Prima di passare all'azione diamo un paio di definizioni:  (1) sia y = f(x)  una certa curva; consideriamo la tangente in suo punto T qualsiasi e prolunghiamola fino a che non intersechi l'asse x nel punto K. Tracciamo da T la perpendicolare all'asse x che lo incontra in H. Il segmento KH viene chiamato sottotangente. (2) Per completezza (anche se a noi interessa poco in questo caso) possiamo anche tracciare la normale alla curva nel punto T (ossia la perpendicolare alla tangente) e prolungarla fino a incontrare l'asse x in N. Il segmento HN viene chiamato sottonormale. Disegniamo il tutto in Fig. 10.

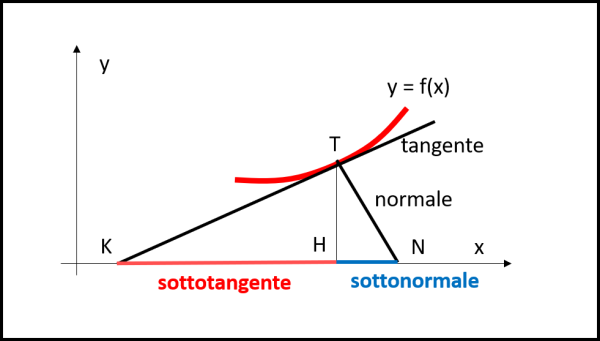
Molto bene. Possiamo adesso disegnare la nostra curva esponenziale di base e con esponente x/a (possiamo sempre ottenere una formula di questo tipo...) e disegniamola in Fig. 11.

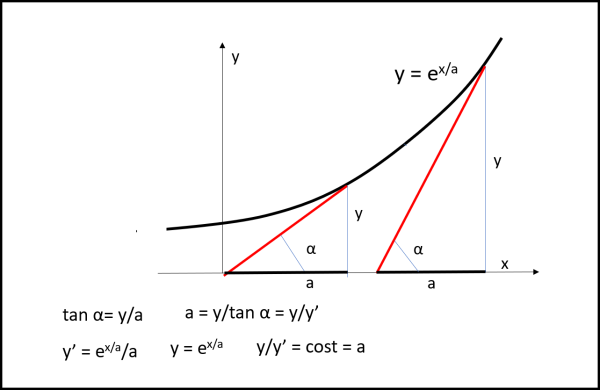
Tracciamo due tangenti (segmenti rossi) qualsiasi e individuiamo le relative sottotangenti. Dobbiamo accettare che i segmenti tangenti prolungati fino all'asse x non danno certamente segmenti uguali (come capitava per la trattrice), ma, in compenso le sottotangenti sono tutte uguali tra loro. Si dimostra facilmente:

y = e^x/a 

y' = tan α = (1/a) e^x/a

Ma sappiamo anche che:

tan α = y/a       (dove a è la sottotangente)

Per cui possiamo scrivere:

y' = y/a

y/y' = a = costante

La sottotangente non cambia mai, qualsiasi sia il punto da cui è stata tracciata la tangente alla curva.

Non ci resta, allora, che far spazzare l'area tra la curva e l'asse x, dal segmento tangente non costante, per ottenere un bellissimo triangolo che ha sempre per base la sottotangente a, come illustrato in Fig. 12.

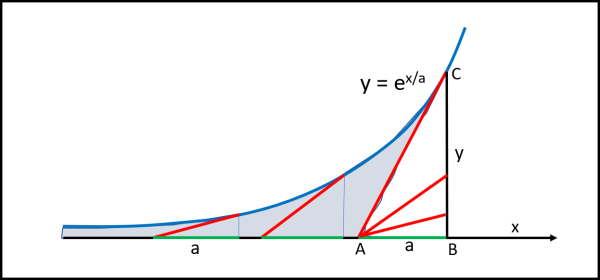
Tracciamo dal punto C che vogliamo la perpendicolare all'asse x e possiamo tranquillamente inserire tutti i triangoli con sottotangente costante come base. L'area spazzata dalla tangente è proprio l'area del triangolo ACB. Tuttavia l'area del triangolo rappresenta solo l'area della parte colorata in azzurro. Per avere l'area totale fino al segmento CB, basta aggiungere un'altra volta l'area del triangolo ABC. Ne segue che l'area tra la curva e l'asse y è uguale a:

A_ESP = 2 ay/2 = ay

Ovviamente y_C è noto perché corrisponde al valore scelto per xB.

Una piccola grande magia senza alcuna equazione differenziale e nemmeno un integrale. Solo la conoscenza della derivata dell'esponenziale e un minimo di trigonometria spiccia.

Facciamo ancora un passo in più e occupiamoci di una curva che è stata profondamente analizzata in questo Circolo: la cicloide.

Ricordiamo, comunque, come si costruisce. Un cerchio viene fatto rotolare senza strisciare su una retta x. La cicloide è la curva descritta da un qualsiasi punto P della circonferenza. Essa potrebbe essere una curva infinita che continua a ripetersi, ma noi consideriamo solo la parte descritta dal punto P (fissato alla circonferenza) durante una rotazione completa del cerchio. Per semplicità si considera come punto P iniziale (e finale)  quello che corrisponde al punto di contatto del cerchio con l'asse x. La vediamo nella Fig. 13.

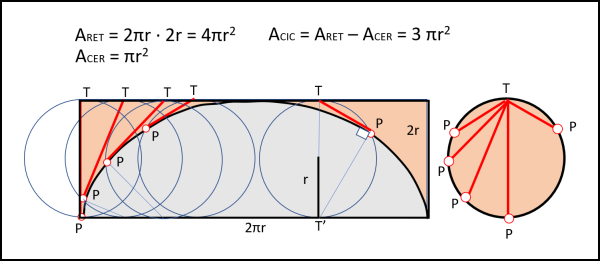
Essa è una curva che ha tante peculiarità, ampiamente trattate in vari articoli, ma in questo caso siamo interessati all'area compresa tra di lei e l'asse x. Ovviamente, si dovrebbe ricavare la sua equazione e integrarla tra i due punti di contatto. Povero Mamikon! No, no, lui risolve tutto in modo semplice ed elegante.

Considera il rettangolo che la contiene e che è tangente al suo massimo. Le dimensioni di tale rettangolo sono ben conosciute: l'altezza è il diametro del cerchio che rotola e la base è la lunghezza della circonferenza. L'area del rettangolo è quindi:

A_RET = 2πr · 2r = 4πr²

per trovare l'area azzurra, basterebbe togliere dall'area del rettangolo l'area rosata... E' difficile calcolarla? Nemmeno per sogno! Dobbiamo solo fare un piccolo ragionamento e per far ciò utilizziamo il cerchio più a destra di tutti (ma potrebbe essere uno qualsiasi). I punti T e T' dividono il cerchio a metà, dato che TT' è un suo diametro. Qualsiasi triangolo che abbia TT' come base e il terzo punto P sulla circonferenza deve essere rettangolo, con l'angolo retto in P. Il segmento PT è quindi perpendicolare a T'P. Tuttavia, T' è il punto di rotazione istantanea di P lungo la cicloide e, quindi, PT è anche la tangente alla cicloide nel punto P. Bene, molto bene! Facciamo muovere il segmento TP in modo che spazzi tutta l'area compresa tra la cicloide e il lato superiore del rettangolo. Questi segmenti non sono certo uguali tra loro, ma, per il teorema generale di Mamikon, l'area spazzata da loro deve essere uguale all'area del loro insieme. Per ottenere questo insieme basta fissare un punto T (a destra) e trasportare tutti i segmenti tangenti, parallelamente a se stessi, fino a far coincidere tra loro tutti gli estremi T. Il punto P descriverà una magnifica circonferenza il cui raggio è proprio r. In altre parole, l'area spazzata di colore rosa è esattamente uguale all'area del cerchio che rotola:

A_CER = πr²

Ne segue:

A_CIC = A_RET - A_CER = 4πr² - πr² = 3πr²

Possiamo concludere, dopo aver solo utilizzato l'area di un rettangolo e quella di un cerchio, che l'area della cicloide (compresa tra la curva e l'asse x) è esattamente tre volte quella del cerchio che rotola! Più semplice di così...

Penso che possa bastare anche se le applicazioni sono ben più numerose e anche ben più complicate (concettualmente, ma non per i calcoli necessari).

Rimarrebbe da dare la soluzione al quiz sulla talpa aliena, che si diverte a portare via un cilindro da ogni pianeta,  lasciando sempre lo stesso volume sul posto, sotto forma di uno strano anello (un po' come quelli che servono per infilare i tovaglioli). MarcoC aveva dato una risposta parziale, ma sicuramente corretta. Tuttavia aveva usato il metodo di sottrazione tra volumi non esponendo chiaramente qual'è il vero succo dell'intero problema. Oltre a quella di MarcoC si può usare un metodo basato su un paio di triangoli e sulla conoscenza del teorema di Pitagora.

Io, però, sono riuscito a risolverlo senza nessun calcolo se non quello della conoscenza del volume di una sfera... e, se ci sono arrivato da solo, penso che molti altri potranno imitarmi. Potremmo chiamarlo metodo di Mamikon a tre dimensioni!

Forza provateci ancora un po', ormai il gioco lo conoscete...

Alla fine sarà anche facile capire la ragione (sicuramente assurda) del comportamento degli strani alieni, ossia quale sia la loro vera motivazione!

Rimandiamo, allora, a una terza puntata l'applicazione di Mamikon alla talpa spaziale...