In questo ultimo articolo riguardo a Mamikon risolviamo, con il solo "calcolo visuale" , il problema relativo  alla talpa spaziale. Possiamo dire di avere introdotto il teorema di Mamikon ... tridimensionale!

Consideriamo le nostre due sfere di raggio diverso. In esse vengono inseriti i due cilindri che avranno anch'essi il raggio di base diverso dato che le altezze dei due anelli sferici, rimasti intatti, devono essere uguali.  Facciamoci aiutare dalla Fig. 14.

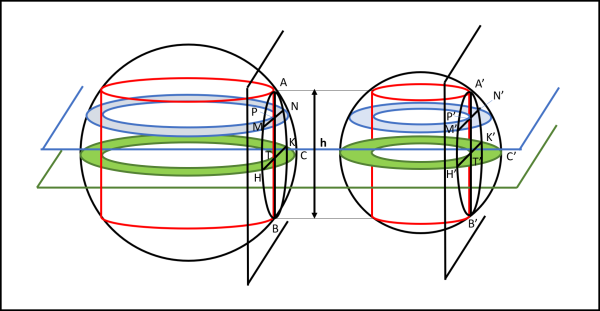
Le due sfere hanno il contorno nero e i cilindri hanno il contorno rosso. Tracciamo un piano perpendicolare all'asse dei cilindri che passi per il cerchio massimo delle sfere (piano con contorno verde). Le sezioni individuano due corone circolari verdi. Come si vede non siamo assolutamente interessati al raggio delle sfera o al raggio delle basi del cilindro: vogliamo solo che AB sia uguale ad A'B', uguali ad h. Prendiamo adesso due piani (neri), perpendicolari al piano precedente che taglino le sfere rimanendo tangenti al cilindro lungo AB e A'B', rispettivamente. Otteniamo due calotte sferiche diverse tra loro. Noi, però, siamo interessati alle circonferenze che i due piani individuano sulle sfere. Queste due circonferenze hanno come diametro AB e A'B', per cui esse sono uguali. in particolare possiamo scrivere che

AB = HK             (diametri della circonferenza, tra loro perpendicolari)

A'B' = H'K'         (diametri della circonferenza, tra loro perpendicolari)

L'area della prima corona circolare verde viene descritta dalla semicorda tangente al cerchio del cilindro, ossia da HT. L'area della seconda corona circolare verde  viene descritta dalla semicorda corrispondente H'T'. Sappiamo, però, che HT = H'T', da cui segue, per il teorema di Mamikon, che esse sono uguali tra loro e hanno la stessa area di un cerchio di raggio AT = A'T' = h/2.

Tracciamo adesso un secondo piano (azzurro) che sia parallelo al piano verde. Anch'esso identificherà due corone circolari azzurre sulle due sfere. Dato che i piani sono paralleli, ne segue che TP = T'P'. Le corde MN e MN', perpendicolari a TP e T'P', rispettivamente, devono essere anch'esse uguali tra di loro. Possiamo scrivere:

MP = M'P'.

L'area delle due corone circolari azzurre sono nuovamente uguali tra di loro. Possiamo concludere che qualsiasi sia il piano parallelo a quello verde, esso individuerà su entrambe le sfere due corone circolari uguali tra loro, di area uguale a quella di un cerchio di raggio uguale alla semicorda corrispondente a MP.

A questo punto possiamo aggiungere, in Fig. 15, una sfera di raggio h/2.

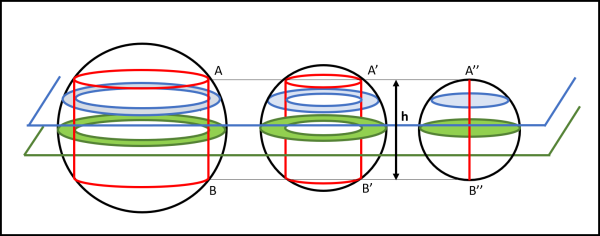
I piani orizzontali paralleli a quello verde individueranno su questa sfera, cerchi di area uguale a quelle delle corone circolari prima descritte. Possiamo perciò dire che le aree determinate da ogni singolo piano sono tutte uguali tra loro. A questo punto basta ricordarsi il Principio di Cavalieri che dice:

Se due solidi hanno uguale altezza e se le sezioni tagliate da piani paralleli alle basi e ugualmente distanti da queste stanno sempre in un dato rapporto, anche i volumi dei solidi staranno in questo rapporto.

Nel nostro caso particolare, l'altezza è pari ad h e le aree stanno nel rapporto 1:1 (ossia sono uguali). Il volume degli anelli sferici rimasti indenni dal passaggio del cilindro deve, perciò, essere uguale a quello di una sfera di diametro h (Fig. 16).

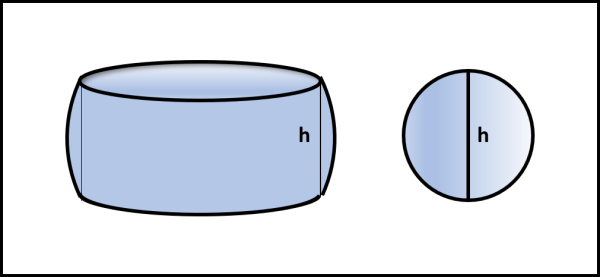
Il volume della sfera è uguale a:

V = (4/3) π h³/8

V =  π h³/6

In parole povere, i nostri alieni hanno la mania di ridurre tutti i pianeti ad avere lo stesso raggio, dato che l'autogravitazione fa collassare tutti gli anelli sferici in sfere perfette di raggio h/2.

Boh... gli alieni sono proprio alieni e hanno un senso della democrazia molto particolare (non è che noi si abbia una visione molto più equilibrata)...