Questo articolo è stato inserito nelle sezioni d'archivio "Matematica e geometria" e "Storia della Scienza"

L'infinito... amore e odio degli antichi greci. Poteva essere l'insieme di un certa quantità di numeri che non finivano mai o doveva essere trattato come qualcosa di concettualmente non misurabile? Vediamo come Galileo tenta di risolvere uno dei grandi paradossi dell'antichità. Per assurdo che sembri, apre la porta al vuoto, alla caduta dei gravi nel vuoto e al calcolo infinitesimale di Newton e Leibniz.

Nei tempi antichi, il termine infinito significava qualcosa senza limiti, ossia illimitato. Il suo grosso problema era perciò l'impossibilità di esaurirsi.  In particolare, Aristotele definiva due tipi di infinito: quello potenziale (in potenza) e quello attuale (in atto).

Consideriamo ad esempio  l'insieme dei punti di una retta. E', sicuramente, infinito, dato che è sempre possibile, dato un certo elemento considerato come limite, trovarne uno successivo (basta pensare al paradosso di Zenone su Achille e la tartaruga). Questa è la sua versione "potenziale": poter andare sempre oltre senza trovare mai un elemento ultimo.  Se, invece, consideriamo un segmento sulla retta, esso ha dei chiari limiti. Tuttavia, tra un punto e l'altro del segmento è sempre possibile inserire nuovi punti.  Passando da un punto a un altro esistono sempre infiniti punti che possono essere considerati tutti assieme. Il segmento è un un insieme di infiniti punti , ma è un infinito "in atto", una infinità compiuta ed esaurita. Il primo infinito è inesauribile, il secondo è qualcosa di compiuto.

Aristotele lo associa a un qualcosa di eticamente negativo, un'espressione dell'incompletezza e di una potenzialità mai attuabile. Perciò lui rifiuta l'idea dell'infinito attuale, anche se non trova modo di eliminarlo da un punto di vista filosofico.

D'altra parte nessuno, a quei tempi, poteva considerare una dimostrazione, impostata sull'infinito, come  logica. Un concetto che era meglio tenere ben lontano dall'ambito della matematica e della geometria.  Da qui, la necessità di cercare ragionamenti,  che evitassero, almeno apparentemente, l'utilizzo dell'infinito.

Ad esempio, nei vari tentativi di quadratura del cerchio, Antifonte tentò di introdurre qualcosa che assomigliava al "limite" attuale. Per lui era possibile iscrivere all'interno della circonferenza un poligono con un numero tale di lati da poter essere considerati piccoli archi di cerchio. Ne seguiva che la circonferenza rappresentava il limite dei poligoni.  Aristotele e la maggior parte dei matematici ritenne del tutto infondata tale ipotesi. Essi asserivano che i poligoni iscrivibili in una circonferenza rappresentano un insieme illimitato, potenziale, dato che per ogni poligono considerato se ne può sempre trovare uno con un numero maggiore di lati. Esiste sempre un poligono  con lati ancora più piccoli, che a sua volta non coinciderà con la circonferenza ma ammetterà dopo di sé un ulteriore poligono. Ne segue che l'insieme dei poligoni non può avere come limite la circonferenza. Se ciò avvenisse, si ammetterebbe  l'infinito attuale e il significato legato alla potenzialità cadrebbe in crisi.

Aristotele pensava, inoltre, che i matematici non avessero alcun bisogno di introdurre grandezze infinite "attuali" nelle loro dimostrazioni. Nel caso dei poligoni e del cerchio era sufficiente ammettere che, dato un qualsiasi poligono, era possibile trovarne un altro con i lati più piccoli, ossia ridurre l'area residua tra poligono e cerchio a una grandezza sempre più piccola, senza immaginare un insieme infinito di poligoni che avesse un qualche limite finito.

Siamo ovviamente caduti nella filosofia pura e l'infinito assume un significato di tipo religioso, una verità non conoscibile se non in potenza. Sappiamo quanto la chiesa fece suo questo concetto e come fosse ovvio per lei mandare al rogo Giordano Bruno con i suoi infiniti mondi.

La Scienza dovette aspettare personaggi come Richard Dedekind e Georg Cantor per risolvere  definitivamente il problema dell'infinito  e dimostrare che l'infinito poteva essere inteso sia nel senso potenziale che in quello attuale. Fatte queste premesse, non voglio certamente affrontare l'opera di Cantor, descritta in modo mirabile, tecnicamente ineccepibile, nella serie di articoli del nostro Umberto e nemmeno  entrare nel faticoso lavoro di concepimento del concetto rigoroso di limite, attraverso grandi geni come Newton, Leibniz, Eulero, Cauchy... vorrei soltanto riproporre un paradosso che si dice inventato dallo stesso Aristotele, proprio per far comprendere l'assurdità del concetto di infinito nell'analisi geometrica antica.

Sto parlando del paradosso della ruota, che è rimasto insoluto per secoli, anche se la sua soluzione è oggi  quasi banale. In particolare, vorrei richiamare il tentativo geniale  di Galileo Galilei, che, in qualche modo, anticipò gli studi successivi ben più rigorosi, pur ammettendo l'impossibilità di una vera soluzione.

Il punto chiave di tutto è un'affermazione di Euclide che dice: "Il tutto non può essere uguale ad una sua parte". Un enunciato che nessuno poteva permettersi di negare, nemmeno lo stesso Galileo. Tuttavia, egli riuscì in qualche modo a raggirarlo arrivando a una conclusione che rimane ancora oggi più che valida, anche se espressa in termini diversi. In qualche modo, egli accetta il fatto che due segmenti, entrambi composti da infiniti punti, possano essere messi in corrispondenza biunivoca senza avere la stessa lunghezza.  Una conclusione apparentemente contraria all'enunciato di Euclide, ma risolta attraverso punti... "vuoti".

Oggi sappiamo, grazie sopratutto a Cantor, che ciò che dice Euclide non è vero quando si parla di insiemi infiniti. In altre parole, lo spazio ha tanti punti quanti un segmento piccolo a piacere. Basta pensare a una semplice corrispondenza biunivoca come quella di Fig. 1.

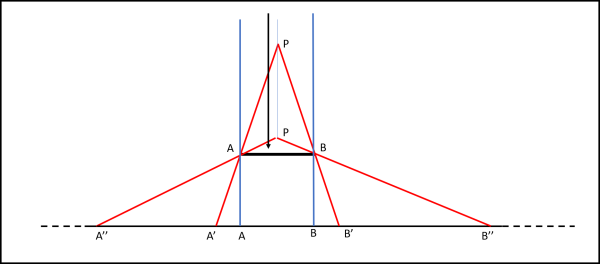
E' sufficiente allontanare o avvicinare il punto di proiezione P dal segmento AB per avere una corrispondenza biunivoca tra AB e qualsiasi altro segmento più grande di AB. In particolare,  se P tende a infinito, la proiezione di AB tende a rimanere uguale ad AB. Se invece P tende a cadere sul segmento AB, la sua proiezione tende ad andare da meno infinito a più infinito. Un discorso che oggi appare semplice, ma che tale non era certo ai tempi di Aristotele e per molti secoli ancora.

Euclide continua, invece, ad aver ragione quando si parla di insieme finiti, che contengano un numero finito di punti. In tal caso se gli insiemi non hanno lo stesso numero di punti, la corrispondenza biunivoca non può esistere. L'esempio di Fig, 2 mostra questa situazione.

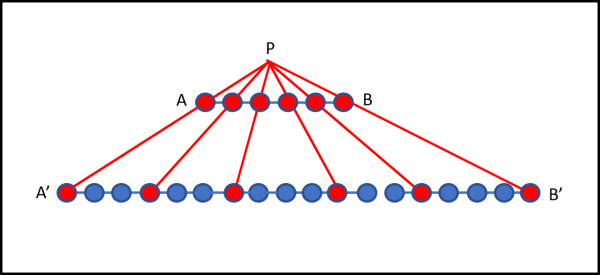
Consideriamo, infatti, AB composto da un certo numero di punti (o particelle) e cerchiamo di proiettarlo sul segmento A'B', non solo più lungo, ma anche  contenente molte più particelle. Ciò risulta impossibile, dato che ogni punto può essere connesso a uno e uno solo. Il problema ricorda quasi perfettamente il problema della ruota pre-Cantor, ma dà a Galileo la possibilità di "saltare", nel vero senso della parola, la difficoltà. In tutto ciò entra in ballo la parola "vuoto", una parola che non si poteva nemmeno nominare (o giù di lì). Galileo la fa invece sua e la sfrutterà alla grande per la geniale deduzione sulla caduta dei gravi. In generale, andando matematicamente a studiare la composizione di un insieme, Galileo affronta il problema ben più fisico della struttura della materia.

Prima di introdurre il paradosso e di seguire la dimostrazione di Galileo, ricordiamo che quest'ultima fa parte della fondamentale opera "Discorsi e dimostrazioni matematiche intorno a due nuove scienze", scritto dopo l'abiura e pubblicata, per ovvie ragioni, nei Pesi Bassi (1938).

E' forse questa l'opera che  lo consacra, più di ogni altra, come vero padre della scienza moderna. È organizzato come un dialogo svolto in quattro giornate fra i tre medesimi protagonisti del precedente Dialogo dei massimi sistemi (Sagredo, Salviati e Simplicio). In particolare si occupa della statica e della resistenza dei materiali per poi passare alla dinamica, con il moto uniforme e quello uniformemente accelerato che lo porterà a stabilire con grande anticipo la caduta dei gravi e la loro uguale velocità nel vuoto. Lo raccomando vivamente ...

Ma torniamo alla  ruota di Aristotele e al suo paradosso.

Consideriamo una ruota perfettamente circolare, al cui interno vi sia un'altra ruota circolare più piccola, che si muova solidalmente con la maggiore. Nell'istante iniziale due punti delle due ruote siano in posizione perfettamente verticale. Essendo le due ruote solidali, la congiungente i due punti deve rimanere rigida. La ruota maggiore inizia a rotolare senza strisciare lungo la linea orizzontale. Entrambi i punti completeranno un giro completo, avendo percorso entrambi la stessa lunghezza, ossia quella della circonferenza maggiore. L'animazione di Fig. 3 mostra ciò che accade.

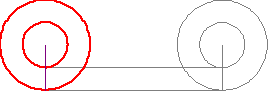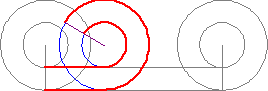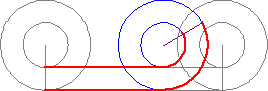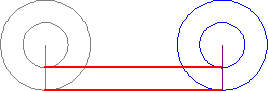
Ma ciò è impossibile, dato che la ruota più piccola ha un raggio minore e quindi anche la sua circonferenza deve essere minore. In altre parole, sembra esistere una corrispondenza perfetta tra i punti dei due cerchi, anche se essi hanno un'estensione diversa, cosa che non poteva verificarsi secondo Euclide.

E quindi  ecco Salviati-Galileo introdurre il problema: “Orsù, già che si è messo mano a i paradossi, veggiamo se in qualche maniera si potesse dimostrare, come in una continua estensione finita non repugni il potersi ritrovar infiniti vacui; e nell'istesso tempo ci verrà, se non altro, almeno arrecata una soluzione del più ammirabil problema che sia da Aristotele messo tra quelli che esso medesimo addimanda ammirandi..."

Le parole infinite vacui sono di per sé una rivoluzione straordinaria...

Galileo affronta il problema, trascurando, in un primo momento, la ruota e lavorando, invece, su due esagoni regolari, in cui uno sia inserito nell'altro, avendo il lato pari alla meta del lato dell'esagono esterno. In poche parole, al posto di due cerchi vi sono due esagoni.

La Fig. 4 ci mostra i due esagoni e l'inizio del movimento di rotolamento.

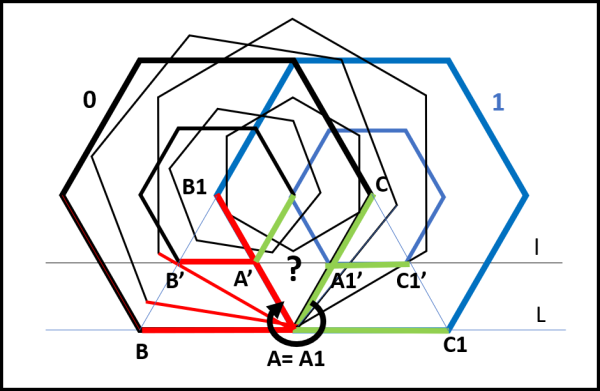
La prima fase vede una rotazione intorno ad A. Il lato AB (rosso) dell'esagono maggiore si porta in AB1 , mentre il suo lato verde (CA) si porta in C1A, prendendo la posizione orizzontale che prima occupava AB. Si noti che A = A1, ossia non si è mosso essendo il punto di rotazione. Ne segue che dopo la prima rotazione l'esagono grande ha percorso esattamente due suoi lati (AB più AC = A1C1).

Cosa capita invece all'esagono piccolo? Il lato rosso B'A' (parallelo ad AB) si porta in A1'C1' (verde), nuovamente in posizione parallela ad A1C1 (verde). Tutto bene? Nemmeno per sogno! Il percorso compiuto dal lato A'B' per arrivare ad A1'C1' NON è assolutamente uguale alla somma di A'B' più A1'C1'. Vi è uno spazio A'A1' in più, che appare come "saltato" nel movimento di rotolamento.

Possiamo vedere in Fig. 5 come questo "strano" comportamento influisca sul percorso totale dei due esagoni (ho colorato i vari lati per meglio seguire il rotolamento).

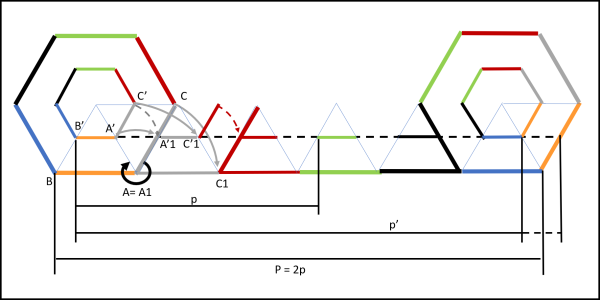
L'esagono maggiore ha percorso esattamente il suo perimetro P. L'esagono minore ha percorso uno spazio ben maggiore del suo perimetro p = P/2. Esso ha aggiunto ad ogni lato un "salto" (uguale come lunghezza al lato) arrivando a compiere il tratto p' che è minore di P (di un tratto uguale al suo lato) o addirittura uguale a P se consideriamo anche il salto successivo all'ultimo lato che deve, comunque, compiere prima di ricominciare il rotolamento con il lato arancione in posizione orizzontale.

A questo punto, possiamo riassumere l'esperimento e confermare che il percorso eseguito dai lati dell'esagono maggiore  è proprio formato dal suo perimetro. Somma dei lati e percorso svolto sulla linea orizzontale sono due segmenti perfettamente uguali come lunghezza e, quindi, possono essere concepiti come due insieme perfettamente uguali, composti dallo stesso numero di punti (Euclide è contento).

Ben diversa è la situazione dell'esagono piccolo (solidale con quello grande). Esso parte in condizioni perfette, ma nel rotolamento il percorso compiuto è decisamente maggiore di quello del suo perimetro, Euclide non è più contento, dato che "il tutto sembrerebbe uguale a una sua parte". E , in fondo, non è contento nemmeno Galileo che non osa contrariare Euclide. Lui realizza che nel movimento dell'esagono piccolo si sono aggiunti dei "salti", che Galileo-Salviati descrive così: "... finita una intera conversione, il maggior poligono avrà calcate [...] sei linee eguali al suo perimetro, senza veruna interposizione; il poligono minore avrà parimente impresse sei linee eguali all'ambito suo, ma discontinuate dall'interposizione de' cinque archi, sotto i quali restano le corde [...] non tocche dal poligono..."

Insomma, una strana discontinuità...

Ci tengo a sottolineare che quello che sembra un puro esercizio di geometria è, in realtà, un problema di carattere fisico dato che i due esagoni fanno parte di un unico corpo solido. Il problema dei "salti" e delle varie corrispondenze sono punti essenziali nella descrizioni della struttura stessa dei corpi solidi.

Galileo fa, poi, il passo decisivo, immaginando di aumentare a dismisura il numero dei lati dei poligoni regolari e dice: "...Passa dunque il gran poligono di mille lati, e misura consequentemente, una linea retta eguale al suo ambito; e nell'istesso tempo il piccolo passa una prossimamente egual linea, ma interrottamente composta di mille particelle eguali a i suoi mille lati con l'interposizione di mille spazii vacui, che tali possiamo chiamargli in relazione alle mille lineette toccate da i lati del poligono..."

Ecco che Galileo inserisce di prepotenza il "vuoto", ossia un numero molto alto di intervalli composti da punti vuoti, appartenenti, comunque, alla linea tracciata dall'esagono piccolo. La sua linea lungo il rotolamento è uguale a quella dell'esagono maggiore, ma invece che da punti reali e un insieme formato da punti reali e da punti "vuoti". Se i lati fossero 100 000, il percorso dell'esagono piccolo sarebbe formato da 100 000 lati piccoli "continui" e da 100 000 segmenti uguali ai lati, ma vuoti.

Dal poligono con migliaia e migliaia di lati al cerchio il passo è breve e Galileo si ripone la domanda: "Or come dunque può senza salti scorrere il cerchio minore una linea tanto maggiore della sua circonferenza? ".

A questo punto Sagredo dà una risposta che oggi sappiamo essere una delle vere soluzioni: "Andava pensando se si potesse dire [...] che punti della circonferenza minore, tirati dal moto della maggiore, andare strascicandosi per qualche particella della linea...". Sagredo ipotizza un trascinamento, che oggi ci può apparire ovvio, ma che allora era un comportamento del tutto da scoprire. Infatti, Salviati-Galileo lo ferma subito: "Questo non può essere [...] perché non sarebbe maggior ragione che alcuno de i toccamenti [...] andassero stracicando per qualche parte della linea , ed altri no ...".

Poi dà la sua spiegazione, più filosofica che matematica, ma che pur non considerandola veramente risolutiva o compresa, apre la porte al vuoto che gli permetterà di descrivere il moto di caduta di un grave, anticipando Newton: "Io ricorrerei alla considerazione de i poligoni sopra considerati, l'effetto de i quali è intelligibile e di già compreso: e direi, che sì come ne i poligoni di cento mila lati alla linea passata e misurata dal perimetro del maggiore, cioè da i cento mila suoi lati continuamente distesi, è eguale la misurata da i cento mila lati del minore, ma con l'interposizione di cento mila spazii vacui traposti; così direi, ne i cerchi (che son poligoni di lati infiniti) la linea passata da gl'infiniti lati del cerchio grande, continuamente disposti, esser pareggiata in lunghezza dalla linea passata da gl'infiniti lati del minore, ma da questi con l'interposizion d'altrettanti vacui tra essi; e sì come i lati  son bene infiniti, così gl'interposti vacui son infiniti: quelli, cioè, infiniti punti tutti pieni; e questi, infiniti punti parte pieni e parte vacui. E qui voglio che notiate, come risolvendo e dividendo una linea in parti numerate, non è possibile disporle in una estensione maggiore di quella che occupavan mentre stavano continuate e congiunte senza l'interposizione d'altrettanti spazii vacui; ma imaginandola risoluta ne' suoi infiniti indivisibili, la possiamo concepire distratta in immenso d'infiniti indivisibili vacui".

Questo insieme composto da punti vuoti e pieni, lo trascina nel problema degli indivisibili che riporta agli atomi di Democrito e ad altre ipotesi ancora aperte e apparentemente irrisolvibili. In realtà Galileo-Salviati conclude con una frase molto vaga e quasi timorosa: "... ricordiamoci che siamo tra gl'infiniti e gl'indivisibili, quelli incomprensibili dal nostro intelletto finito per la lor grandezza, e questi per la lor piccolezza. Con tutto ciò veggiamo che l'umano discorso non vuol rimanersi dall'aggirarsegli attorno; dal che pigliando io ancora qualche libertà, produrrei
alcuna mia fantasticheria, se non concludente necessariamente, almeno, per la novità, apportatrice di qualche maraviglia. "

Vale la pena mostrare in Fig. 6, il disegno originale di Galileo riguardo al paradosso della ruota:

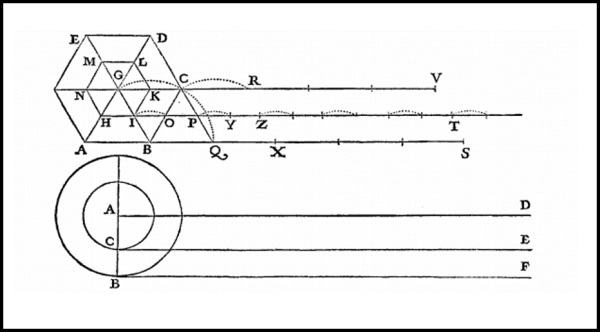
Galileo non può dare una dimostrazione risolutiva, ma comprende che questo tipo di analisi lo porterà a grandi scoperte: una vera e innovativa descrizione della struttura della materia, che, sebbene a prima vista estremamente "fantasiosa" e quasi "infantile", avrà ricadute fondamentali sull'esistenza del vuoto.

Per il momento, comunque, conclude: "Queste son di quelle difficoltà che derivano dal discorrer che noi facciamo col nostro intelletto finito intorno a gl'infiniti, dandogli quelli attributi che noi diamo alle cose finite e terminate; il che penso che sia inconveniente...".

In realtà, Giordano Bruno aveva già dimostrato chiaramente quanto fosse veramente INCONVENIENTE e ben si comprende quanto fosse "terribile" per la chiesa, data la sua assoluta fiducia in Aristotele.

Riassumendo l'intera descrizione potremmo dire che la ragione che permette alle due linee tracciate da un punto della ruota esterna e da uno corrispondente di quella interna di essere uguali durante il rotolamento risiede nel fatto che il percorso della ruota piccola consiste in  infiniti punti intervallati da infiniti spazi vuoti infinitamente piccoli, mentre il percorso di quella grande consiste solo di punti e non di spazi vuoti.

In particolare, la possibilità dell'esistenza del vuoto – prevista da Democrito – viene ritenuta una seria ipotesi scientifica e proprio nel vuoto Galileo sostiene giustamente che tutti i corpi "discenderebbero con eguale velocità", in opposizione alla scienza contemporanea che riteneva l'impossibilità del moto nel vuoto e, di conseguenza, non poteva che seguire Aristotele e credere fermamente che la velocità di caduta dipendesse dalla massa dell'oggetto.

Ricordiamo che Aristotele  riteneva che per mantenere in moto un oggetto fosse necessaria l’applicazione continua di una forza. Secondo il grande filosofo, una freccia in movimento creava una sorta di vuoto dietro di sé e l’aria, che si precipitava IMMEDIATAMENTE a riempirlo, spingeva la freccia in avanti: il terrore del vuoto, diventato una vera ossessione per la chiesa. Come conseguenza, Aristotele affermava che corpi differenti cadono con velocità differenti: la velocità dipende dal loro peso. Maggiore è il peso e maggiore è la velocità di caduta. Purtroppo, questa affermazione sembra confermata dalle osservazioni, e, ancora oggi, è diffusa fra la maggior parte della popolazione mondiale (non per niente gli astronauti sulla Luna hanno mostrato che il vuoto galileiano esisteva e che una piuma e un martello cadevano realmente con la stessa velocità).

Essere riusciti, come ha fatto Galileo, a ipotizzare una caduta nel "malefico" vuoto, e di aprire le porte alla rivoluzione newtoniana è veramente un capolavoro assoluto del pensiero umano!

In generale, nei Discorsi Galileo apre un nuovo e irresistibile interesse riguardo alla composizione del "continuo"  e delle quantità infinitesime  che porterà, attraverso studiosi come Cavalieri e Torricelli, allo sviluppo del calcolo infinitesimale  di Newton e Leibniz. .

La soluzione del paradosso della ruota ha oggi più di una soluzione.

La prima si appoggia proprio alla frase di Sagredo, che Salviati-Galileo boccia subito.  In realtà, da un punto di vista fisico, la ruota più piccola non rotola senza strisciare! Lei ruota e striscia nel contempo... Possiamo facilmente pensare a un esempio di tutti i giorni per confermarne la verità: basta pensare alle ruote di un automobile. Esse hanno un certo diametro e rotolano normalmente sulla strada. All'interno delle ruote si trova il coprimozzo, che può simulare benissimo il cerchio più piccolo e che normalmente sembra rotolare come la ruota. Provate, però, a parcheggiare troppo vicino al marciapiede, in modo che il coprimozzo (aggettante) vada a toccare il marciapiede, come illustrato dalla Fig. 7 (in cui in alto vi è la visione di fronte e in basso quella dall'alto).

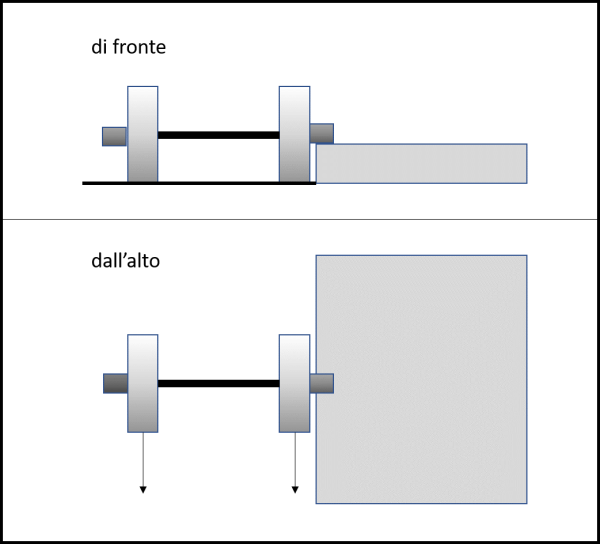
Se il coprimozzo rotolasse come la ruota principale dovrebbe continuare a farlo anche sul marciapiede e, invece, si sente nitidamente il rumore stridente tipico dello "strisciamento", anche se le tracce lasciate sia sul marciapiede che sulla strada hanno la stessa lunghezza.

Sagredo, aveva ragione, dato che Galileo, con la sua analisi, aveva evidenziato che il tutto avveniva come se la ruota piccola compiesse infiniti salti di ampiezza infinitesima, prima di arrivare al termine della corsa. Questi salti sono, in fondo, quelli corrispondenti allo strisciamento.

Un'altra soluzione, puramente geometrica, fa ricorso al percorso compiuto da un punto P della circonferenza durante il rotolamento. Stiamo parlando ovviamente della cicloide, che ormai conosciamo molto bene. In questo caso, il punto della ruota più piccola descrive una cicloide accorciata, la quale compie un percorso nettamente più breve. Il centro, invece, va esattamente in linea retta. i tre punti percorrono orizzontalmente il percorso uguale alla circonferenza massima, ma il loro effettivo percorso avviene secondo le cicloidi e quella del cerchio minore è nettamente più corto di quello della ruota più lunga. Il centro sceglie la linea più diretta, il punto della ruota piccola compie un percorso più lungo e quello della ruota grande ancora di più. In tal modo essi riescono a ritrovarsi nella stessa identica posizione iniziale dopo un rotolamento completo (Fig.

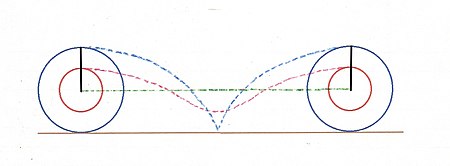
In modo ancora più semplificato (fisico) si può dire che il centro è comune alle due ruote e che se esso percorre un certo tragitto, ogni punto delle due ruote deve compiere un tragitto uguale (proprietà della traslazione di un solido).

Vale anche la pena ricordare che ciò che capita per il rotolamento della ruota maggiore, capiterebbe anche se a rotolare fosse la ruota più piccola. Nel primo caso avremmo un trascinamento forzato della più piccola da parte della più grande, nel secondo una frenata della più grande da parte della più piccola. Basta guardare la Fig. 9,  dove utilizziamo nuovamente una ruota e il suo mozzo... In alto chi comanda il moto è la ruota grande, in basso è invece la ruota piccola. Anche questa figura, in fondo, risolve il paradosso.

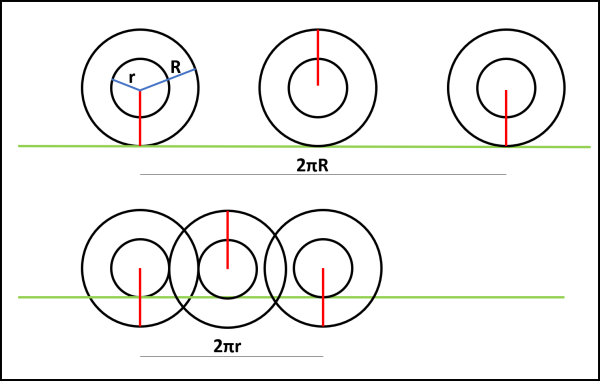
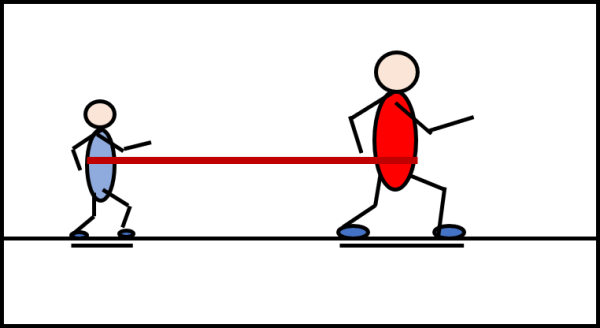
Non ci sarebbe nemmeno bisogno di far rotolare qualcosa... pensate a un adulto legato in modo rigido a un bambino. Il passo dell'adulto è lungo il doppio di quello del bimbo. Se l'adulto andasse al suo ritmo il bimbo verrebbe in gran parte TRASCINATO. Se fosse il bimbo a dettare il ritmo, l'adulto sarebbe frenato...

Grande Galileo!