Categorie: Curiosità Matematica
Tags: espressione matematica quiz tempo limite
Scritto da: Vincenzo Zappalà
Commenti:19
Un quiz rapidissimo **
Ci sono espressioni matematiche che sembrano praticamente irrisolvibili, soprattutto se si richiede la soluzione in un tempo molto breve... proviamo a fare un esempio...
No spaventatevi... quello che vi chiedo è di trovare il risultato della espressione che segue...
Il vero problema è che dovrete farlo in meno di cinque minuti (orologio alla mano!) e senza usare calcolatrici... insomma del tutto "a mente" (diciamo così).
Veniamoci incontro... non datemi la soluzione, ma ditemi il tempo che avete impiegato. Poi daremo anche la soluzione...


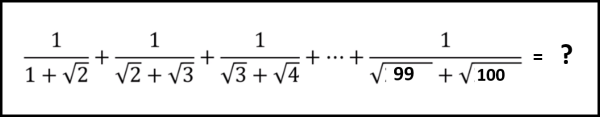




19 commenti
2:45, di botto. Poi circa 7 min per rifarlo al computer. Mi sa che è ora di smettere di usare fortran e passare a qualche cosa di più moderno.
Devo ammettere che mio figlio ha fatto da poco le espressioni più semplici con le radici, e ho pensato subito alla risoluzione. Qualche mese fa ci avrei messo più tempo
1:05 col computer ... ho rinunciato alla soluzione mentale
Conta solo se fatto a mente e senza calcoli... (poi Francesco ci spiegherà come c'è riuscito... ma, per adesso, continuate a provare SENZA computer e senza qualsiasi specie di calcolatrice)
Anzi... potete anche darmi la soluzione dell'espressione... senza dire però come avete fatto a risolverla senza calcolatore o cose del genere...
A me 99
9?
Una coincidenza. Le somme parziali In corrispondenza della radice di 4, 9, 16 ,25, 36…...100.
Si, scusa, ho pigiato due volte. Solo 9
Facciamo chiarezza,,,
Sarebbe bello sapere il risultato e il tempo impiegato senza alcun calcolatore..
Francesco 9 2:45
Marco68
Fabrizio 9 5
GuanFranco
Dai, riempiamo i buchi...
Mi arrendo
Dalle 22:38 alle 22:43 di ieri segnati dal PC.
Il risultato dovrebbe essere 9 , però ho usato carta e penna perchè a mente non avevo visto le semplificazioni da fare. Tempo impiegato: circa 60min.
caro MarcoC,
io non ho detto di farlo a mente, ho solo detto di non usare il calcolatore o la calcolatrice. Un po' di carta e penna ci vuole (ma in solo 5 minuti...). Un aiutino? Ricordiamoci i prodotti notevoli!
va bene... a questo punto mi dite come avete fatto a risolverlo senza calcolatrici e con un minimo di carta e penna?
Io l'ho risolto abbastanza velocemente, perchè ho una certa idiosincrasia nei confronti di alcuni numeri (quelli che io chiamo bruttini) e perchè mio figlio a scuola ha appena studiato alcuni argomenti che mi hanno aiutato.
Ci sono alcuni numeri che non riesco a guardare: 0.428571... è proprio brutto e non mi dice nulla. Vuoi mettere 3/7? Semplice
Analogamente non riesco a pensare a 1.414213..., è radice(2), e così lo lascio scritto.
Poi una radice al denominatore mi appare come il parmigiano sugli spaghetti allo scoglio: devo fare di tutto per portarla al numeratore. Quindi il lato di un quadrato con diagonale d nota, per me non si scrive d/radice(2), ma d*radice(2)/2.
Considerando poi che mio figlio ha appena fatto i prodotti notevoli, mi è venuto subito in mente che (a+b)*(a-b)=a^2-b^2
Quindi il passo è stato veloce:
Prima applico la proprietà commutativa dell'addizione ai denominatori (questo per evitare successivamente dei denominatori negativi, che sono pure loro inguardabili):
1/(1+rad(2))+1/(rad(2)+rad(3))+....=1/(rad(2)+1)+1/(rad(3)+rad(2)+....
Poi moltiplico il numeratore ed il denominatore di ogni addendo per il rispettivo prodotto notevole in modo da far sparire la radice al denominatore:
1/(rad(2)+1)=(rad(2)-1)/((rad(2)+1)*(rad(2)-1))=(rad(2)-1)/(2-1)=rad(2)-1
Quindi al denominatore appare sempre 1 ed al numeratore la differenza tra i termini del denominatore (prima del prodotto notevole)
rad(2)-1+rad(3)-rad(2)+rad(4)-rad(3)+.....+rad(100)-rad(99)
Le varie radici sono una volta con il segno + ed una volta con il segno -
Resta soltanto:
-1+rad(100)=-1+10=9
Ciao
Finalmente la matematica dell'orologio! Altro che quella di Gauss...
Stesso modo di Francesco. Forse reminiscenze remote dell'algebra studiata a scuola.
La lampadina si è accesa quando ho afferrato che le radici a denominatore si prestavano ad essere rimosse moltiplicando e dividendo ciascun termine per la differenza degli addendi. Tutti i denominatori erano uguali a 1 o -1 a secondo di come si mette il meno tra i due termini. A numeratore rimaneva una catena di radici che però si annullavano a vicenda. Rimanevano solo il primo e l'ultimo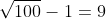 .
.
Il termine generico è
La catena di termini diventa:
OTTIMO amici !!!!