Categorie: Fisica classica
Tags: asse di rotazione assi principali d'inerzia asteroidi astronauta sovietico effetto Džhanibekov ellissoide a tre assi energia cinetica Iperione momenti d'inerzia momento angolare ribaltamento ribaltamento della Terra segreto assoluto stabilità teorema racchetta da tennis
Scritto da: Vincenzo Zappalà
Commenti:16
L' Effetto Džhanibekov: Dagli asteroidi alla stazione spaziale e a una racchetta da tennis **
Questo articolo è presente nella sezione d'archivio Dinamica e Meccanica (all'interno di Fisica Classica)
Passare da un asteroide a una racchetta da tennis, anche se attraverso la stazione spaziale, non è un piccolo salto... ma quando c'è di mezzo il momento d'inerzia tutto è possibile.
Il fenomeno che voglio descrivere era già noto da più di cent'anni, ma è stato riscoperto e messo in evidenza su una stazione spaziale sovietica. Noi cominciamo, però, dagli asteroidi...
Immaginiamo di assimilare la forma di un asteroide con un ellissoide a tre assi (cosa di cui abbiamo già parlato QUI). Come per qualsiasi altro solido si può dimostrare (ma non lo faremo adesso) che esistono tre direzioni, tra loro ortogonali, per le quali il momento della quantità di moto (o momento angolare) è parallelo all'asse di rotazione. Questi sono detti assi principali di inerzia e i corrispondenti momenti di inerzia sono detti momenti principali di inerzia. Per un ellissoide a tre assi è facile determinarli ed essi sono proprio quelli relativi ai tre assi dell'ellissoide (a, b, c con a>b>c).
Facendolo ruotare ci accorgeremmo che la rotazione è stabile solo per il massimo (attorno a c) e il minimo momento (attorno ad a). Per quello intermedio la stabilità va a farsi benedire e la rotazione è caotica. In realtà, la soluzione comunemente raggiunta dagli asteroidi è quella relativa al massimo momento d'inerzia, dato che è quella che comporta anche la minima energia cinetica.
N.B: Tanto per richiamare vecchi concetti, esiste una semplice relazione tra momento angolare e momento d'inerzia (ricordate la ballerina sul ghiaccio che allarga e stringe e braccia?) ed è data da:
L = I ω
Il che vuol dire che se aumento il momento d'inerzia I (braccia larghe), dovendo restare costante il momento angolare L, la velocità angolare ω deve diminuire e viceversa.
In Fig. 1 disegniamo il nostro asteroide triassiale (a sinistra) e vediamo come viene visto assumendo che il suo asse di rotazione (a destra) sia diretto verso di noi.
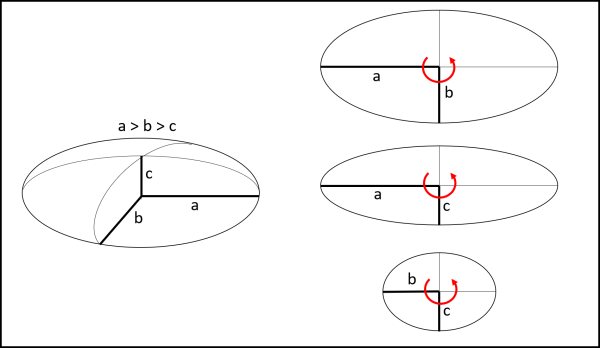
Si ha il massimo momento d'inerzia (minima velocità angolare) quando l'asse di rotazione coincide con c. Questa è la configurazione normale (stabile). Come già detto sarebbe teoricamente stabile anche la soluzione in cui la rotazione avviene attorno ad a (minimo momento d'inerzia = massima velocità angolare), ma la ricerca "naturale" della configurazione con la minima energia favorisce di gran lunga il momento massimo. Non sarebbe invece stabile la rotazione attorno all'asse b in quanto porterebbe a un momento d'inerzia intermedio. Quando ciò dovesse capitare si avrebbe un moto caotico, come succede, ad esempio, per Iperione (il satellite di Saturno) o per diversi asteroidi molto piccoli (collisione avvenuta recentemente).
Guardiamo come ruota Iperione e riflettiamo.
Per Iperione la caoticità del moto è legata anche alle risonanze con il pianeta, ma in generale possiamo vedere che si notano veri e propri ribaltamenti del satellite. Questo è il fenomeno che c'interessa maggiormente...
Passiamo, allora, a vedere ciò che capita in un ambiente a microgravità come una stazione spaziale. Il video che segue mostra cosa capita a una vite (o qualcosa del genere) che ruoti secondo un asse che non sia il suo massimo o minimo momento d'inerzia. Sembra veramente un gioco di prestigio! Un fenomeno già riportato "teoricamente" nel lavoro del francese Poinsot nel 1850, confinato nel dimenticatoio, ma che è stato riscoperto "praticamente" dall'astronauta russo Vladimir Aleksandrovič Džhanibekov nel 1985, tanto che oggi viene anche chiamato effetto Džhanibekov.
Attorno a questa "riscoperta" vi è stato un decennio di segretezza assoluta da parte sovietica, dato che tutta la faccenda è legata proprio alla non stabilità del momento d'inerzia intermedio. Si pensò a livello scientifico: "E se la Terra non stesse girando attorno al suo massimo momento d'inerzia? Dovremmo aspettarci prima o poi un ribaltamento di 180° con conseguenze catastrofiche globali?". Oggi sappiamo che la Terra è sicuramente stabile nella sua rotazione (ma la cosa non era del tutto ovvia, dipendendo anche dalla distribuzione della massa interna). In ogni modo l'effetto Džhanibekov è stato poi chiamato anche teorema della racchetta da tennis, dopo un articolo del 1991 uscito quando ancora il segreto della notizia dell'astronauta sovietico era mantenuto molto stretto.
Mentre la spiegazione matematica dell'effetto non è banale e mi permetto di evitarla, anche se in pratica non è altro che una veloce o lenta variazione dell'asse che porta a una nuova configurazione che non è comunque quella di minima energia e quindi il ribaltamento si ripete continuamente, non è invece assolutamente difficile realizzarla a casa nostra (o in un prato) pur patendo fortemente la gravità.
Intorno a noi vi sono moltissimi oggetti con tre assi principali d'inerzia. Un qualsiasi parallelepipedo come un libro o un... cellulare (lo consiglio vivamente dato che si rischia anche di fracassarlo e non sarebbe male!) sono capaci di riprodurlo. Tuttavia, rimaniamo nel classico e utilizziamo una racchetta di tennis da tavolo (più maneggevole di una racchetta da tennis). Se la ruotiamo attorno al manico (minimo momento d'inerzia) o attorno ad un asse perpendicolare alle facce della racchetta (massimo momento d'inerzia) tutto rimane stabile e la rotazione si mantiene (malgrado la gravità faccia finire in fretta l'esperimento). Ma se la facciamo ruotare attorno ad un asse perpendicolare al lato lungo della racchetta considerata "di piatto", il moto diventa chiaramente instabile e si noterà che velocemente si verifica un ribaltamento di 180° della racchetta. La Fig. 2 riassume meglio di tante parole i tre assi principali.
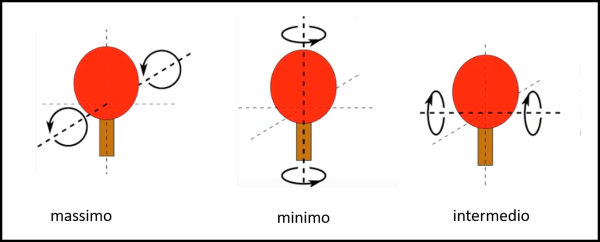
Il video che segue mostra molto bene come quanto detto sia realmente verificabile da chiunque. Buon divertimento, soprattutto sapendo che la Terra non farà la stessa fine...
P.S.: spero che Arturo (per gli amici l'uomo del palloncino!) non se lo lasci scappare!
A proposito di moti caotici, QUI parliamo dello strano caso di un asteroide (o cometa?) alieno...






16 commenti
Nei video si vedono gli oggetti ruotare "molto" velocemente.
Mi chiedevo se questa rotazione instabile si manifesta solo per valori di omega oltre una certa soglia? oppure si verificano per ogni valore di omega?
Grazie.
caro MarcoC,
la stessa cosa della vite succede alla racchetta da tennis nel giro di poche rotazioni e a velocità decisamente bassa.
Sicuramente nei calcoli entra anche la velocità di rotazione (energia cinetica), ma questo non cambia la instabilità della situazione, al limite potrebbe far variare i tempi dei ribaltamento, allo stesso modo, però, gioca anche la distribuzione della massa e il momento d'inerzia...
Mi sto chiedendo del tempo che passa tra un'inversione e l'altra (mi aspetto una relazione che tenga conto della velocità angolare, oltre che ovviamente della distribuzione di massa, come già dici).
Poi voglio riprendere l'esame di meccanica razionale, perché vedo molte analogie con il problema delle vibrazioni che si instaurano in un'albero con eccentrico che gira (sto pensando ad un pezzo sul tornio durante la sua lavorazione: nelle sedi dei cuscinetti delle morse e della contropunta si creano forze trasversali alternate, talvolta di natura simile alle forze impulsive, ma le ho sempre riferite alla combinazione tra l'eccentricità di massa del pezzo e la sua rigidezza in una certa direzione). Certo, sulla terra c'è sempre la gravità e poi il pezzo che si studia è sempre appoggiato/incernierato, altrimenti cade. Ma potrebbe essere interessante nel moto di un proiettile o anche in quello di un tuffatore. Ci voglio ragionare un po'
Ciao e grazie: come al solito riesci a risvegliare l'interesse dello studentello che ero.
Sono molto contento Francesco! Devo cercare, ma non è difficile trovare la trattazione analitica accurata... forse su wikipedia (edizione inglese). Tuttavia, non è banale e ho preferito evitare...
Prova qui...
https://en.wikipedia.org/wiki/Tennis_racket_theorem
Si, l'avevo visto. Sul testo di meccanica razionale era trattata la questione, ed è probabile che da lì mi venga in mente l'esempio del tuffatore. Grazie
caro Francesco,
l'esempio del tuffatore... beh, normalmente lui ruota attorno al massimo momento d'inerzia o il minimo, quando fa gli avvitamenti. Tienimi informato...
Molto bello ed esemplificativo. Pensando al tuffatore ed a certi tuffi che si vedono in televisione mi pare che occorra il caso in cui il tuffo si svolge prima con una rotazione attorno ad un asse con massimo momento d'inerzia per poi finire con la rotazione attorno ad un asse con minimo momento. Interviene anche la modificazione della geometria e della distribuzione delle masse del tuffatore quando questi si piega/torce, ma in generale direi che il passaggio attraversa condizioni di instabilità. Forse una delle difficoltà del tuffatore è anche quella di cercare di "domare" il passaggio da una rotazione stabile ad un'altra?
Ora la difficoltà nello studio del tuffatore credo che stia proprio nel fatto che non è un corpo rigido, sposta i suoi assi: in una capriola rannicchiata probabilmente l'asse di inerzia fianco dx-fianco sx rimane simile a quando sta ritto (ovviamente, come la ballerina, cambia la velocità), ma se la capriola la fa carpiata (piegamento in modo da portare la testa verso i piedi, a gambe stese) allora l'asse si sposta verso le ginocchia. Poi probabilmente l'asse intermedio (diciamo approssimativamente ombelico-schiena) non è poi cosi diverso da quello fianco-fianco (siamo abbastanza dei cilindri).
Per fare avvitamenti inoltre torciono il busto e portano le braccia in maniera molto asimmetrica (una sopra la testa, l'altra davanti al petto)
Indubbiamente passano per punti di non equilibrio, altrimenti non si moverebbero (oppure proseguirebbero in moto uniforme intorno al loro baricentro).
Quello che intendevo dire era che questi cambi continui degli assi di inerzia sono responsabili delle loro figure e dei repentini ribaltamenti che fanno, o più facilmente subiscono perché quando sono in aria non ci sono appoggi su cui fare reazione. Purtroppo il libro è in soffitta da mia suocera e mi ci vuole un po' a recuperarlo. Era una raccolta di dispense e dubito che sia in rete,ma più ci penso e più mi sembra di aver già visto queste trattazioni (in fin dei conti anche nei link di Enzo si dice che è un fenomeno già conosciuto da circa 150 anni)
Sicuramente l'essere elastico aiuta nel cambiamento del proprio momento d'inerzia da istante a istante. Un po' come le supernove e la contrazione del diametro... La velocità del cambiamento influisce abbastanza poco sulla instabilità momentanea, ma probabilmente la trattazione accurata dovrebbe tenerne conto... Iperione ci m ostra un bel ... tuffo!
Tenetevi pronti a camminare con una formica, avendo tanto tempo davanti a voi...
Certo, un passo alla volta: prima corpi rigidi per i quali il moto del corpo è più facilmente descrivibile (mto del baricentro + moto intorno al baricentro), poi corpi elastici (cioè rigidi ma che si deformano sotto forze esterne in maniera elastica, con piccoli spostamenti relativi che tornano a zero quando la forza cessa), poi corpi plastici (che restano deformati, quando togli le forze), poi meccanismi (un po' come le bielle-manovelle dei motori), poi meccanismi di corpi deformabili con forze interne (come sono gli uomini). Sembra di vedere il programma del triennio di ingegneria dei vari corsi di meccanica e costruzioni. Ma la base stava nel corso di meccanica razionale che, a quanto mi riferiscono, non si fa nemmeno più. E tutto nasce sempre da Newton (F=ma).
Vedi come Iperione, un cacciavite, una racchetta da tennis, il movimento dell'uomo sono tutti legati e grazie ad uno che portava la parrucca per coprire i pidocchi ma che ha avuto la curiosità di guardare pianeti e stelle, ora siamo qui a ragionarci?
splendide riflessioni, caro Francesco, e ti ringrazio di cuore!!
E se questo effetto fosse legato alla inversione dei poli magnetici?
Al centro della terra c'è un ambiente a microgravità e se il nucleo è composto da metallo fluido non perfettamente simmetrico può occorrere in questo fenomeno..
beh visto che i poli stanno migrando sempre più velocemente ora saremo vicini al "salto"
Mha, qui stiamo parlando solo di cinematica, la dinamica credo entri in campo solo successivamente come effetto di ordini successivi. E non penso che siano da valutare effetti elettromagnatici, ma solo di meccanica classica. Cioè, stiamo parlando semplicemente di una trottola a tre assi d'inerzia.
Sono d'accordo con Francesco... l'elettromagnetismo non c'entra nel fenomeno, che rimane essenzialmente di meccanica.
Sto leggendo un libro che accenna alla possibilità, individuata da Laskar, che Venere abbia subito dei capovolgimenti a causa del caos presente nel suo moto. Possibilità che potrebbe spiegare la diversa rotazione del pianeta.
Questa ipotesi ha a che vedere con il fenomeno descritto in questo articolo?
Direi di no Fabrizio... Il caso di Venere (e non solo) è dovuto all'instabilità dell'asse di rotazione per effetto delle perturbazioni planetarie e mareali (anche dello stesso Sole). La nostra Terra ha un inclinazione di 23° che si mantiene costante (a meno di circa un paio di gradi) per merito della Luna che ci stabilizza con le sue maree. Se non ci fosse la Luna oscilleremmo fino a 80° rispetto ai 23° odierni. Sono calcoli fatti proprio da Laskar...
Questo capita anche se la rotazione avviene secondo un asse principale.