Gli altri articoli di questa serie (LA SFERA DI POINCARÉ) , li trovate nel'archivio--> Matematica e geometria-->Matematiche pure

Per chi non conosce il differenziale di una funzione.

Un concetto base, nella definizione di varietà differenziabile, è proprio il differenziale. Per chi non lo conosce, possiamo introdurlo in modo grafico-intuitivo. Diciamo intanto che riguarda le funzioni fra spazi euclidei, dove abbiamo due o più coordinate. Ricordo che con n indichiamo la dimensione della varietà. Ci limiteremo al caso  n=1 o n=2 di linee o superfici. Ciò nonostante, questo è valido anche per n=3 o superiore, ma non possiamo fare rappresentazioni grafiche.

Forse la terminologia può spaventare, ma  il differenziale in un punto della varietà altro non è che una semplice funzione lineare (nel caso n=1 una retta, nel caso n=2 un piano, nel caso n>=3 semplicemente un "iperpiano")  tangente in quel punto alla varietà.

si dice poi che una funzione è differenziabile, se in ogni punto ammette differenziale  (nel caso n=1 per trovare il differenziale dobbiamo calcolare la derivata, nel caso n=2 una matrice di derivate parziali).

Partiamo da una superficie parametrizzata definita localmente

Come sempre in matematica,  le cose nate da esigenze più o meno pratiche, diventano poi dei concetti generalizzati.

E' poi importante ricordare il percorso storico di quella che si chiama superficie fino ad arrivare alle varietà.

Vediamo  allora come veniva definita  una superficie( o meglio un elemento di superficie) in :

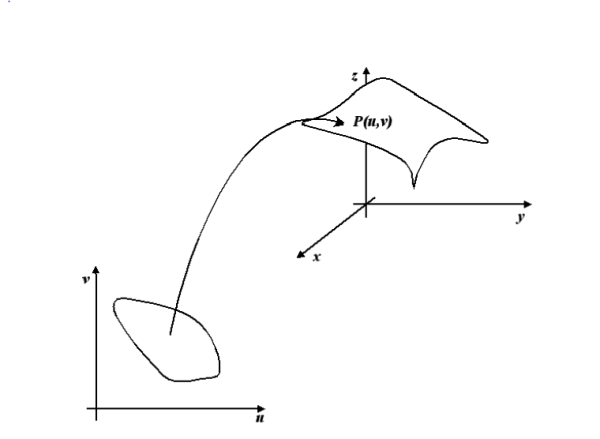
Ricordando  la topologia, possiamo parlare di carte,  ossia di omeomorfismi  fra un aperto del piano e un aperto dello  spazio .  Visto che abbiamo a che fare con aperti dello spazio euclideo, possiamo esplicitare facilmente questi omeomorfismi,  che indichiamo con :

usando ad esempio delle funzioni parametriche:

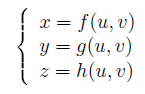
che dipendono appunto dai parametri u,v.

Nello spirito di quanto detto sopra, richiediamo (senza entrare oltre nei particolari) che questi elementi di superficie ammettano piano tangente, ovvero che le funzioni  siano differenziabili.

Richiami sulle varietà topologiche

la definizione di varietà topologica richiede quella di spazi di Hausdorff:

Spazi di  Hausdorff

Uno spazio topologico S è detto di Hausdorff se per ogni coppia x, y di elementi distinti di S esistono un intorno di x e un intorno di y disgiunti. In tal caso lo spazio si dice separato.

Come si può facilmente verificare, ogni spazio metrico è di  Hausdorff. Non è però vero in generale per ogni spazio topologico.

Noi tratteremo in questo contesto solo Spazi di  Hausdorff.

Facciamo un riassunto dell'articolo sulle varietà topologiche che trovate per esteso qui.

Ricordiamo  la definizione di spazio localmente euclideo, che è alla base della definizione di varietà topologica:

Uno spazio topologico X si dice localmente euclideo se ogni suo punto x ha un intorno aperto Ui  omeomorfo a un disco aperto  in .  Chiamiamo 

cerchiamo dunque degli insiemi aperti e delle funzioni omemorfe (biettive, continue, con inversa continua). Ebbene,una varietà topologica è costituita da uno spazio topologico connesso (fatto di un solo pezzo), di Hausdorff, e localmente euclideo . E una varietà differenziabile? Semplice:

Una varietà differenziabile è una varietà topologica in cui ogni carta locale che compone l'atlante(unione delle carte) della varietà sia differenziabile.

Se prendiamo  l' esempio della costruzione dell'atlante del cerchio ricordiamoci ancora una volta che il cerchio è una varietà topologica; osserviamo però che è qualcosa di più; il cerchio infatti possiede in ogni punto una retta tangente; questo lo sappiamo da sempre. Il cerchio passa perciò di grado, e diventa una  varietà differenziabile.  Intuitivamente , una varietà differenziabile è una varietà topologica  liscia, cioè  senza rugosità, senza punte.

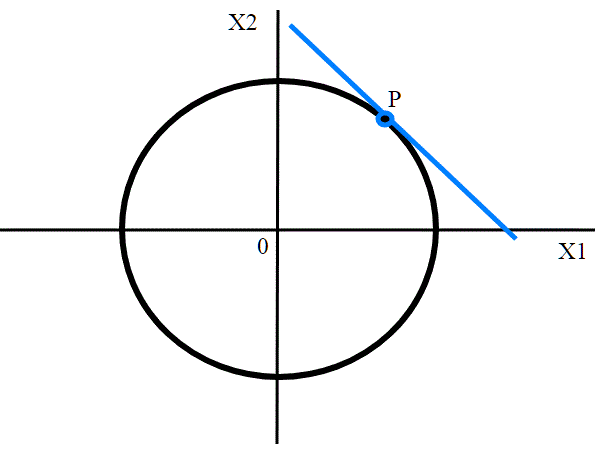
Nel caso  del quadrato le cose invece non vanno  così.

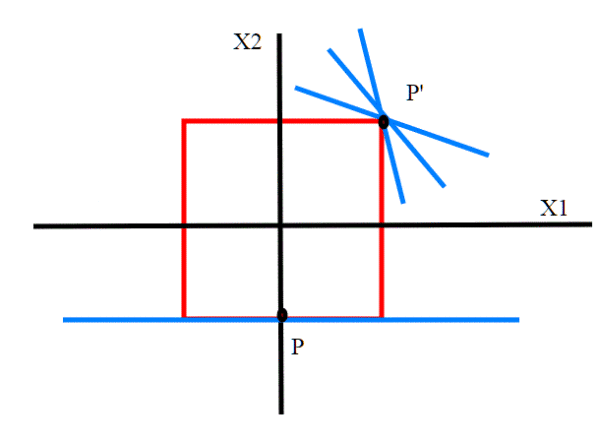
Pur essendo il quadrato una varietà topologica di dimensione 1, in esso non è possibile come per il cerchio definire  la tangente (il differenziale) in ogni punto. Nei punti interni si, ma negli spigoli no.

Perché sono importanti le varietà differenziabili?

Con i requisiti richiesti, la varietà, ovvero il nostro spazio in questione , ammette differenziale in ogni punto. Pensiamo al caso n=2; possiamo in ogni punto trovare il piano tangente alla nostra varietà, che in questo caso è una superficie. Ora, potrebbe presentarsi il problema di misurare la lunghezza di una linea sulla superficie. Consideriamo allora i piani tangenti alla linea; su di essi possiamo definire un pezzettino di distanza riguardante la sua lunghezza. Poi, con un procedimento di integrazione, possiamo sommare tutti questi pezzetti, ottenendo la lunghezza cercata. Abbiamo, con questo sistema, ridotto la metrica della curva a quella dei piani tangenti, che stanno in .  Lo scopo del prossimo articolo sarà proprio di parlare di un altro tipo di varietà, ossia di quelle dotate di metrica. Concludo   lasciando ai più teorici la definizione formale di varietà differenziabile:

Definizione formale di varietà differenziabile nel caso generale.

Risulta intuitivo definire una varietà differenziabile quando le funzioni di transizione sono differenziabili.

Nel caso generale, abbiamo una superficie ricoperta da un atlante. Consideriamo due aperti di tale atlante che non abbiano intersezione nulla, Ui, Uj e i corrispondenti omeomorfismi  in . Quindi, se , le carte relative avranno diverse coordinate nello spazio euclideo, come per gli archi del cerchio.

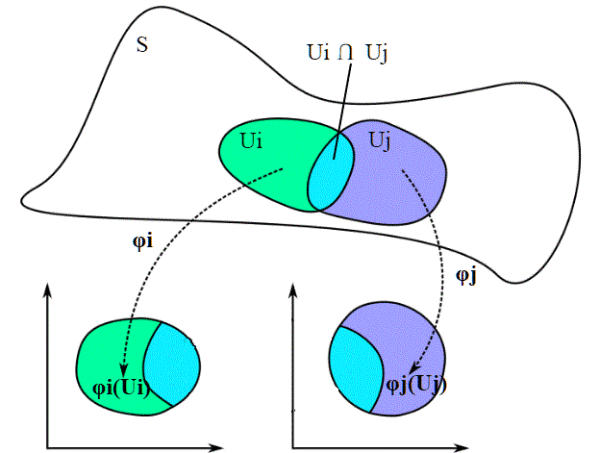
Chiamiamo , e  le rispettive immagini dell'intersezione   tramite i due diversi omeomorfismi. Vogliamo costruire una funzione  che dia la corrispondenza fra le coordinate.

Essendo  un omeomorfismo, essa è biunivoca, quindi ammette inversa :

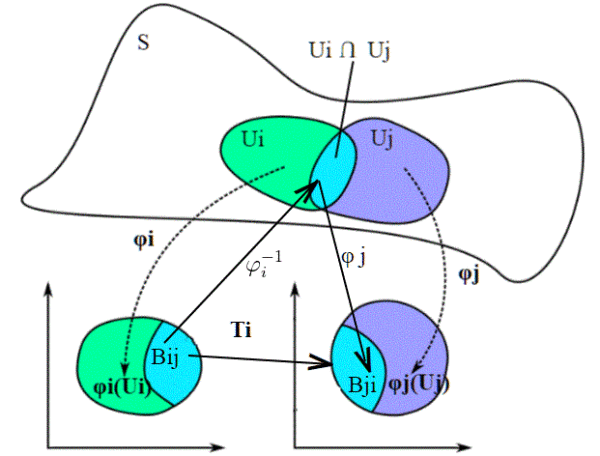
dopodiché, con , andiamo da   in :

; componendo  adesso le due funzioni, ottengo Ti:

.

Non abbiamo fatto tutto questo lavoro per niente; siamo partiti da una varietà topologica, in cui non c'è alcuna struttura di ma solo gli intorni definiti dalla topologia. Abbiamo costruito una funzione  che è un omeomorfismo. Da qui nasce storicamente un innalzamento di struttura:  essendo le funzioni Ti di transizione definite e a valori in , ha senso richiedere che siano differenziabili. Se tutte le Ti  dell'atlante di una varietà topologica sono differenziabili allora la varietà diventa una varietà differenziabile. 

Gli altri articoli di questa serie:

0) Un progetto ambizioso

1. LE OMOTOPIE E LA SEMPLICE CONNESSIONE
2. L'ENUNCIATO DELLA CONGETTURA.
3. Le TRI-Varietà topologiche