Per risolvere il quiz basta ricordarsi dei prodotti notevoli... niente di più!

Ricordiamone uno dei più usati:

(a + b)(a - b) = a² - b²

Cerchiamo di farlo "entrare" nella nostra espressione...

Consideriamo il suo termine generico: 1/(√k + √(k + 1))

cominciamo a scriverlo come:

1/(√(k+ 1) + √k)

Un banalissimo passaggio... Adesso moltiplichiamo sopra e sotto per: 1/(√(k + 1) - √k)

(√(k + 1) - √k)/((√(k+ 1) + √k)(√(k + 1) - √k)) = (√(k + 1) - √k)/((k+1) - k) = (√(k + 1) - √k)/1

A denominatore abbiamo usato il prodotto notevole citato prima e si è trasformato in 1.

Il termine generico è quindi diventato : √(k + 1) - √k

Basta pensare al termine successivo e salta subito all'occhio cosa succederà...

√(k + 1) - √k + √(k + 2) - √(k + 1)

- √k + √(k + 1) - √(k + 1) + √(k + 2)

Il termine √(k + 1) si elimina con quello successivo uguale e cambiato di segno. E così via... in  modo tale che di tutta la somma rimanga solo il primo termine cambiato di segno più l'ultimo.

Vediamo cosa succede scrivendo proprio i numeri. La nostra somma originaria

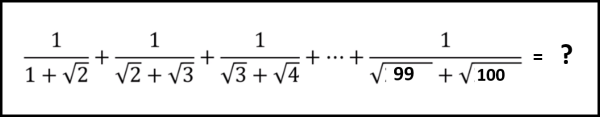
è diventata

(- √1 + √2) + ( - √2 + √3) + (- √3 + √4) + .... + (- √99 + √100)

- √1 +  √100 = - 1 + 10 = 9

Come trovato da vari lettori (praticamente questa è la copia dell'ultimo commento di Fabrizio).

BRAVI tutti!

QUI il quiz