Categorie: Fisica classica Relatività Storia della Scienza
Tags: caduta dei gravi discorsi Einstein esperimento mentale Galileo principio di equivalenza relatività generale vuoto
Scritto da: Vincenzo Zappalà
Commenti:5
Due esperimenti mentali che hanno cambiato la fisica ***
Questo articolo è stato inserito nella pagina d'archivio "La caduta libera" compresa nelle sezioni "Dinamica e meccanica" e "Relatività Generale"

Parliamo ancora una volta di Galileo e della sua legge di caduta dei gravi nel vuoto. Abbiamo visto che egli era riuscito a scacciare da sé la paura del “vuoto”, inserendolo in qualche modo all’interno della ruota piccola che ruotava solidalmente con quella grande. In qualche modo, non solo aveva gettato i primi semi per i concetti matematici di limite e di insieme finito e infinito, ma l'aveva usato "fisicamente" proprio per analizzare la struttura dei materiali e il loro moto.
Il punto di arrivo più grande è, però, la deduzione che il vuoto sia da considerare una realtà a tal punto che solo al suo interno si possa realmente verificare che i corpi nella loro caduta non sono assolutamente influenzati dalla propria massa. Essi seguono tutti la stessa legge e questa dipende solo e soltanto dal tempo al quadrato, ossia si è di fronte a un moto uniformemente accelerato, dovuto alla "gravità".
Vale la pena estrarre qualche parte dei suoi “Discorsi” per vedere soprattutto come egli smonta con un esperimento mentale, geniale nella sua semplicità, la visione aristotelica. Già di per sé una conquista di eccezionale importanza e di pari coraggio.
La caduta dei gravi di Galileo
L’inizio della trattazione viene data a Sagredo.
Sagredo: … A quella del vacuo vorrei sentir ben ponderare la dimostrazione d'Aristotele, con la quale ei l'impugna, e quello che voi, Sig. Salviati, gli opponete. Il Sig. Simplicio mi farà grazia di arrecar puntualmente la prova del Filosofo, e voi Sig. Salviati, la risposta.
Sagredo chiede espressamente a Simplicio di dimostrare l’assunto di Aristotele e a Salviati di contrapporgli qualcosa di valido e alternativo.
Simplicio: Aristotele, per quanto mi sovviene, insurge contro alcuni antichi, i quali introducevano il vacuo come necessario per il moto, dicendo che questo senza quello non si potrebbe fare. […] A questo contrapponendosi Aristotele, dimostra che, all'opposito, il farsi […] il moto distrugge la posizione del vacuo […]. Fa due supposizioni: l'una è di mobili diversi in gravità, mossi nel medesimo mezzo; l'altra è dell'istesso mobile mosso in diversi mezzi. Quanto al primo, suppone che mobili diversi in gravità si muovano nell'istesso mezzo con diseguali velocità, le quali mantengano tra di loro la medesima proporzione che le gravità; sì che, per esempio, un mobile dieci volte più grave di un altro si muova dieci volte più velocemente. Nell'altra posizione piglia che le velocità del medesimo mobile in diversi mezzi ritengano tra di loro la proporzione contraria di quella che hanno le grossezze o densità di essi mezzi; talmente che, posto, v. g., che la crassizie (densità, consistenza) dell'acqua fusse dieci volte maggiore di quella dell'aria, vuole che la velocità nell'aria sia dieci volte più che la velocità nell'acqua. E da questo secondo supposto trae la dimostrazione in cotal forma; Perché la tenuità del vacuo supera d'infinito intervallo la corpulenza, ben che sottilissima, di qualsivoglia mezzo pieno, ogni mobile che nel mezzo pieno si movesse per qualche spazio in qualche tempo, nel vacuo dovrebbe muoversi in uno istante; ma farsi moto in uno instante è impossibile; adunque darsi il vacuo in grazia del moto è impossibile.
Simplicio-Aristotele è estremamente chiaro. Innanzitutto ribadisce ciò che è sotto gli occhi di tutti: i corpi più pesanti cadono più velocemente al suolo. Stabilisce una proporzionalità diretta tra peso e velocità. Poi analizza come uno stesso corpo cadrebbe se si cambiasse il mezzo attraverso cui si muove (acqua, aria, olio, …). Nuovamente l’esperienza diretta ci dice che più il mezzo è denso e più lentamente cade l’oggetto. Egli assume, perciò, che se la densità dell’acqua fosse dieci volte maggiore di quella dell’aria, la velocità dell’oggetto sarebbe dieci volte minore. Ne segue, in pratica, una formula del tipo:
V = P/D (V velocità, P peso, D densità del mezzo)
Da questa formula conclude logicamente che se il mezzo si rarefacesse sempre di più, fino a raggiungere il vuoto, il corpo cadrebbe a velocità grandissima, ossia “in uno istante”. E ciò è chiaramente impossibile.
Salviati: … quanto concluda la dimostrazione d'Aristotele, mi par che si potrebbe andar contro a gli assunti di quello, negandogli amendue
E Sagredo inizia a porre qualche dubbio
Sagredo: Ma io, Sig. Simplicio, che n'ho fatto la prova, vi assicuro che una palla d'artiglieria, che pesi cento, dugento e anco più libbre, non anticiperà di un palmo solamente l'arrivo in terra della palla d'un moschetto, che ne pesi una mezza, venendo anco dall'altezza di dugento braccia.
Ed ecco che Galileo-Salviati, preparatogli il terreno adatto, introduce il suo innovativo modo di affrontare la realtà, ossia attraverso l’esperimento; in altre parole, attraverso un’esperienza fatta in una situazione controllata e quindi misurabile. Ad Aristotele basta l’esperienza a livello qualitativo, per Galileo è fondamentale la quantificazione. Galileo sente l'esigenza di considerare l'esperienza in condizioni ideali e rigorosamente determinabili, di eliminare tutti i fattori di disturbo rispetto al fenomeno che deve essere studiato.
Tuttavia, Salviati smonta le conclusioni di Simplicio, proprio analizzando situazioni legate all’esperienza osservabile da tutti. E lo fa in modo veramente geniale…
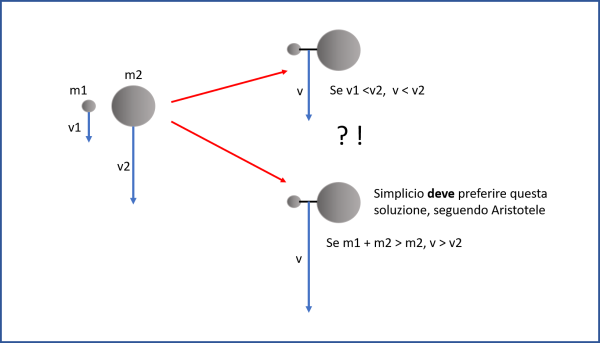
Salviati: Quando dunque noi avessimo due mobili, le naturali velocità de i quali fussero ineguali, è manifesto che se noi congiugnessimo il più tardo col più veloce, questo dal più tardo sarebbe in parte ritardato, ed il tardo in parte velocitato dall'altro più veloce. Non concorrete voi meco in quest'opinione?
Salviati suppone di collegare il corpo più veloce a quello più lento e conclude che in tal modo il corpo, nato dalla loro unione, deve avere una velocità intermedia. O, in altre parole, il più lento verrebbe accelerato e il più veloce ritardato. Simplicio non può che confermare… e cade nel tranello.
Salviati: Ma se questo è, ed è insieme vero che una pietra grande si muova, per esempio, con otto gradi di velocità, ed una minore con quattro, adunque, congiugnendole amendue insieme, il composto di loro si moverà con velocità minore di otto gradi: ma le due pietre, congiunte insieme, fanno una pietra maggiore che quella prima, che si moveva con otto gradi di velocità: adunque questa maggiore si muove men velocemente che la minore; che è contro alla vostra supposizione. Vedete dunque come dal suppor che 'l mobile più grave si muova più velocemente del men grave, io vi concludo, il più grave muoversi men velocemente.
Simplicio: Io mi trovo avviluppato, perché mi par pure che la pietra minore aggiunta alla maggiore le aggiunga peso, e aggiugnendole peso, non so come non debba aggiugnerle velocità, o almeno non diminuirgliela.
Salviati: Qui commettete un altro errore, Sig. Simplicio, perché non è vero che quella minor pietra accresca peso alla maggiore.
Simplicio: Oh, questo passa bene ogni mio concetto.
Salviati: Non lo passerà altrimente, fatto ch'io v'abbia accorto dell'equivoco nel quale voi andate fluttuando: però avvertite che bisogna distinguere i gravi posti in moto da i medesimi costituiti in quiete. Una gran pietra messa nella bilancia non solamente acquista peso maggiore col soprapporgli un'altra pietra, ma anco la giunta di un pennecchio di stoppa la farà pesar più quelle sei o dieci once che peserà la stoppa; ma se voi lascerete liberamente cader da un'altezza la pietra legata con la stoppa, credete voi che nel moto la stoppa graviti sopra la pietra, onde gli debba accelerar il suo moto, o pur credete che ella la ritarderà, sostenendola in parte? […] Concludete pertanto che nella libera e naturale caduta la minor pietra non gravita sopra la maggiore, ed in consequenza non le accresce peso, come fa nella quiete.
Simplicio: Ma chi posasse la maggior sopra la minore?
Salviati: Le accrescerebbe peso, quando il suo moto fusse più veloce: ma già si è concluso che quando la minore fusse più tarda, ritarderebbe in parte la velocità della maggiore, tal che il loro composto si moverebbe men veloce, essendo maggiore dell'altra; che è contro al vostro assunto. Concludiamo per ciò, che i mobili grandi e i piccoli ancora, essendo della medesima gravità in spezie, si muovono con pari velocità.
Simplicio: Il vostro discorso procede benissimo veramente: tuttavia mi par duro a credere che una lagrima di piombo si abbia a muover così veloce come una palla d'artiglieria.
L’esperimento mentale di Galileo mette decisamente in crisi Simplicio e tutta la teoria aristotelica sulla caduta dei gravi. Il ragionamento quasi diabolico di Galileo può essere così riassunto:
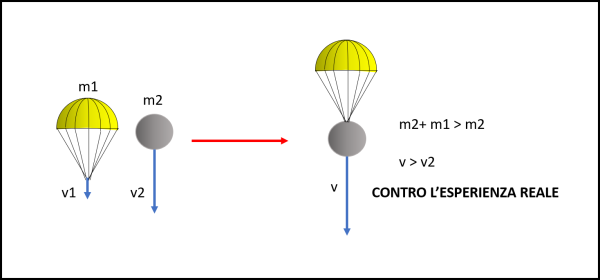
- Aristotele dice che il corpo più pesante arriva al suolo prima di quello più leggero.
- Leghiamo insieme i due corpi con una corda sottile.
- Quello più leggero e lento dovrebbe ostacolare la caduta di quello più pesante e dovrebbe farlo andare più piano.
- Tuttavia, è anche vero che mettendo assieme i due corpi se ne ottiene un terzo più pesante che dovrebbe andare più veloce se avesse ragione Aristotele.
- La stessa cosa dovrebbe succedere se su una palla di cannone venisse attaccata una sostanza meno densa. La massa aumenterebbe e nuovamente la velocità dovrebbe essere maggiore. Aristotele non può che avere torto.
I risultati sono incompatibili fra loro. Ciò è inaccettabile e, quindi, si deve ammettere che l’idea di partenza è sbagliata. Mezzi diversi, attrito diverso, forma, peso a riposo e in moto … troppe variabili “nascoste” impediscono un esperimento “puro”.
Con un esperimento ideale Galileo ha distrutto la teoria ed ora non gli resta che inventarne una nuova che attraverso un esperimento reale dimostri che la velocità di caduta dipenda solo e soltanto dal tempo. Ma l’esperimento reale deve seguire i vincoli dell’esperimento ideale, nel modo migliore possibile, permettendo altresì di quantificare l’intero processo. Non lo può certo eseguire facendo cadere due gravi dalla Torre di Pisa, dato che sarebbe del tutto simile all’esperienza su cui si basava la teoria di Aristotele. O, quantomeno, non potrebbe certo usare una piuma e una sfera di ferro, dato che non potrebbe controllare l’attrito su materiali diversi. D’altra parte, se usasse oggetti dello stesso materiale, poco sensibile all'attrito, avrebbe difficoltà insormontabili nella misura dei tempi di caduta (con i mezzi di allora). E’ giunta l’ora di usare percorsi quasi completamente privi di attrito e, nel contempo, di materiale tale da risentirne al minimo. Ma, soprattutto, di “rallentare” la caduta… Ed ecco l’invenzione sublime del piano inclinato…
Einstein e l’esperimento della cassa nel vuoto
Facciamo un salto di tre secoli, siamo di nuovo vicinissimi a una rivoluzione epocale ed Einstein vuole riassumere in poche parole il passaggio dalla relatività dei sistemi inerziali (galileiana) alla relatività ben più generalizzata, introducendo le accelerazioni e la forza di gravità. Di fronte a lui si pone, comunque, il problema delle due masse, quella inerziale e quella gravitazionale. Ciò che vuole dimostrare Einstein, però, non è tanto l’uguaglianza tra massa inerziale e massa gravitazionale, già registrata dalla meccanica classica, ma riuscire a interpretarla.
L’esperimento mentale di Einstein vuole proprio giungere a questo scopo e, nel contempo, dimostrare la validità di un principio generale di relatività (valido per qualsiasi sistema di riferimento).
Einstein immagina una larga porzione di spazio vuoto, così lontana da astri e da altre masse di grandezza apprezzabile, da fornirci approssimativamente le condizioni richieste dal principio fondamentale di Galileo, ossia un riferimento rispetto al quale i punti siano in quiete o in moto rettilineo uniforme.
Come sistema di riferimento, Einstein immagina “una spaziosa cassa che assomigli a una stanza, avente al suo interno un osservatore e molti apparecchi”. Nel mezzo del soffitto viene inserito un gancio esterno con una corda. Un essere (“alieno”, immaginiamo noi) comincia a tirare la corda con una forza costante, ossia con costante accelerazione. Un osservatore esterno vedrà la cassa andare a velocità sempre più grande, ma cosa sta pensando l’osservatore all’interno della cassa?
“L’accelerazione di detta cassa gli verrà trasmessa dalla reazione del pavimento della medesima […]. Egli sta dunque in piedi nella cassa esattamente come chiunque sta in piedi in una stanza di una casa della nostra terra. Se egli lascia andare un corpo che prima teneva in mano, l’accelerazione della cassa non sarà più trasmessa a questo corpo, e per tale ragione, il corpo si dirigerà verso il pavimento con un moto relativo accelerato”. In poche parole, l’uomo penserà di trovarsi, insieme con la cassa in un campo gravitazionale costante.
Einstein prosegue: “Egli (l’uomo) per un momento si chiederà con stupore come mai la cassa non cade in questo campo gravitazionale. Proprio allora però, egli scopre il gancio nel mezzo del coperchio e la corda che vi è attaccata, e di conseguenza ne conclude che la cassa è sospesa immobile nel campo gravitazionale. Dobbiamo sorridere di questa persona e dire che essa sbaglia nelle conclusioni che trae? Io credo che non possiamo farlo se vogliamo essere conseguenti; dobbiamo invece ammettere che il suo modo di concepire la situazione non contrasta né con la ragione né con le leggi note della meccanica. Sebbene la cassa risulti accelerata rispetto allo “spazio galileiano” poco fa preso in esame, possiamo nondimeno considerarla come in quiete. Abbiamo così delle buone ragioni per estendere il principio di relatività fino a corpi di riferimento che sono accelerati uno rispetto all’altro, e abbiamo così guadagnato un potente argomento a favore di un postulato di relatività generalizzato.”
Einstein dimostra che le leggi della meccanica, valide per un corpo in quiete immerso in un campo gravitazionale, sono le stesse che agiscono su un corpo in moto accelerato. Non esiste un criterio oggettivo, indipendente dall’osservatore e dal luogo in cui si trova, per dire se la cassa e il suo occupante sono in moto accelerato oppure se sono immobili, sospesi all’interno di un campo gravitazionale. Sia l’osservatore che sta nella cassa sia quello che si trova all’esterno ritengono corretta la propria interpretazione: moto e quiete non sono dunque condizioni assolute, ma stati relativi, dipendenti da ciò che ciascun osservatore sperimenta intorno a sé. Nel nostro caso, osservare la cassa dall’interno o dall’esterno cambia completamente le conclusioni a cui giunge l’osservatore.
Il passo successivo dell’esperimento porta Einstein a scoprire che massa inerziale e massa gravitazionale sono esattamente come due facce di una stessa medaglia:
Supponiamo che questa persona dentro la cassa fissi una corda al lato interno del coperchio, e appenda un corpo all’estremo libero della corda. Il risultato sarà che la corda verrà tesa in modo da pendere “verticalmente” all’ingiù. Se chiediamo la sua opinione sulla causa della tensione della corda, la persona risponderà: “Il corpo sospeso subisce una forza all’ingiù nel campo gravitazionale e questa è neutralizzata dalla tensione della corda; ciò che determina la misura della tensione della corda è la massa gravitazionale del corpo sospeso.” Invece, un osservatore che si libri senza vincoli nello spazio interpreterà i fatti così: “La corda deve per forza prendere parte al moto accelerato della cassa, e trasmette questo moto al corpo appeso ad essa. La tensione della corda è tanto grande quanto occorre per produrre l’accelerazione del corpo. Ciò che determina la misura della tensione è la massa inerziale del corpo”. Guidati da quest’esempio, vediamo che la nostra estensione del principio di relatività fa apparire necessaria la legge dell’uguaglianza fra massa inerziale e massa gravitazionale. Abbiamo ottenuto così un’interpretazione fisica di questa legge.
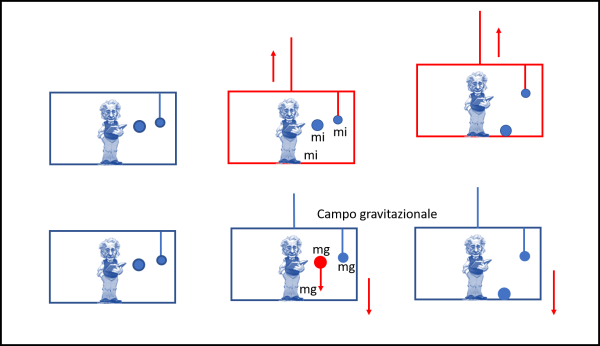
In basso, ciò che conclude chi è all'interno. La cassa è in quiete con i suoi occupanti. Improvvisamente, si instaura un campo gravitazionale diretto verso il basso. Einstein e le due palline cominciano a cadere, ma il pavimento (per Einstein) e la corda (per la pallina sospesa) li fermano. La pallina libera cade sul pavimento e viene fermata. Ovviamente, Einstein si accorge che vi è una corda esterna che blocca la cassa nel suo moto dovuto al campo gravitazionale. Le masse di Einstein e delle due palline sono masse gravitazionali, perché stanno obbedendo alla legge di gravitazione.
Ecco dunque che la corrispondenza tra massa inerziale e massa gravitazionale non è più un accidente casuale come nella gravità newtoniana, ma una conseguenza necessaria del principio di relatività: ciò che appare all’osservatore esterno come resistenza inerziale al moto, è giudicato con altrettanto diritto effetto di un campo gravitazionale dall’osservatore all’interno della cassa.
Il principio di equivalenza così definito è un elemento fondamentale della relatività generale: se tutti i corpi non cadessero con la stessa velocità all’interno di un campo gravitazionale, non sarebbe più possibile scambiare le conseguenze di un moto accelerato qualsiasi per quelle dell’azione di un campo gravitazionale.
È importante infine precisare che l’esperimento mentale proposto da Einstein vale solo a livello locale, cioè se l’osservatore si trova in una regione di spazio sufficientemente piccola come è appunto l’interno di una cassa.
Possiamo, perciò, tornare al celebre vagone in moto uniforme, imprimendo ad esso un'accelerazione (o decelerazione). Se il moto del vagone non è uniforme, chi è dentro subisce una forte spinta in avanti (se il moto è decelerato). Il comportamento meccanico dei corpi all’interno del vagone si manifesta all’osservatore interno in modo ben diverso rispetto a quello rivelato quando è in moto uniforme. Il principio di relatività galileiano non può applicarsi al vagone che si muove di moto non uniforme. Ciò farebbe pensare a una specie di realtà fisica assoluta al moto non uniforme, in opposizione al principio generale di relatività appena dimostrato. Tuttavia, Einstein dimostra che ciò non è assolutamente vero.
Ecco le sue parole: “E’ certamente vero che l’osservatore situato nel vagone ferroviario percepisce una spinta in avanti come risultato della frenata, e che egli riconosce in ciò la non uniformità del moto del vagone, Nessuno però lo costringe a riferire questa spinta ad una reale accelerazione (positiva e negativa) del vagone. Egli potrebbe anche interpretare così la sua esperienza: “Il mio corpo di riferimento (il vagone) rimane perennemente in quiete. Rispetto ad esso, tuttavia, esiste (durante il periodo di funzionamento dei freni) un campo gravitazionale che è diretto in avanti e che è variabile rispetto al tempo. Sotto l’influenza di questo campo, la banchina insieme con la terra si muove di moto non uniforme in maniera tale che la sua velocità originaria diretta all’indietro viene continuamente ridotta. Questo campo gravitazionale è anche quello che imprime la spinta all’osservatore”
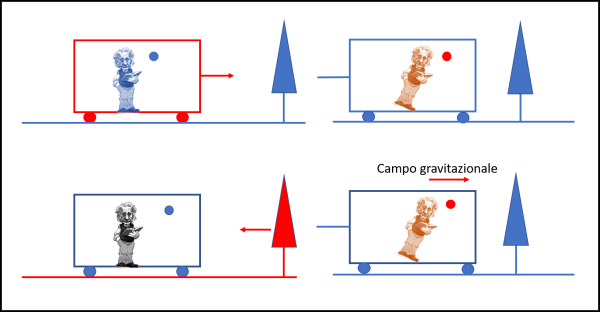
In basso, chi occupa il vagone si considera fermo e vede muovere verso di lui albero e terreno. Ciò che è dentro al vagone rimane in quiete. Improvvisamente si instaura un campo gravitazionale diretto versa destra. Il campo impone un movimento uguale e contrario all’albero e al terreno, per cui loro risultano fermi. Nuovamente, viene applicata una corda al vagone che lo rende immobile nel campo gravitazionale. Ne segue che gli unici che si muovono in avanti sotto l’azione del campo gravitazionale sono Einstein e la pallina.
Tra i due esperimenti mentali sono passati circa tre secoli e, in tale periodo è vissuto nientemeno che Newton. Tuttavia, sia nella sua semplicità quasi ironica (Galileo) sia nella apparente banalizzazione dell’introduzione a qualcosa di completamente rivoluzionario (Einstein), i due personaggi rimangono geni assoluti. L’unica differenza è che Galileo riuscì a rendere reale il suo esperimento con i piani inclinati, mentre Einstein dovette aspettare molto tempo prima che qualcuno potesse osservare le ricadute reali del suo esperimento mentale. E, ancora oggi, è continuamente messo sotto esame…






5 commenti
Mi ha colpito questa frase di Galilei:
Sembrerebbe una anticipazione degli argomenti di Einstein. Ma forse è una interpretazione da "postero" di Galilei ed in particolare di Einstein, che non è possibile attribuire alla affermazione di Galilei.
Forse c'era un legame, diciamo , "quantistico" tra i due. . Aldilà dello scherzo non può che evidenziarsi un continuum tra due Grandi Scienziati; due grandi che hanno costruito in tempi diversi (proprio come Work in progress) una grande teoria che , compòletata appunto al momento da Eistein, continua a ricevere conferme su conferma, in attesa di un'altro Grande che la definisca e unifichi finalmente.
. Aldilà dello scherzo non può che evidenziarsi un continuum tra due Grandi Scienziati; due grandi che hanno costruito in tempi diversi (proprio come Work in progress) una grande teoria che , compòletata appunto al momento da Eistein, continua a ricevere conferme su conferma, in attesa di un'altro Grande che la definisca e unifichi finalmente.
cari amici,
sicuramente non possiamo a dare a Galileo segni di preveggenza (doveva ancora arrivare Newton...), ma sicuramente tra i grandi c'è sempre un segno di continuità. Ricordiamo cosa diceva il Vasari: "Giotto posò il pennello che raccolse dopo molti decenni Masaccio...".
Ancora una volta mi trovo a sottolineare una mancanza del sistema educativo scolastico di base: non si insegna ai ragazzi il meccanismo dell'"esperimento mentale" e le notevoli potenzialità che esso racchiude. Infatti, anche a livello liceale, l'impatto con la fisica classica è generalmente duro anche per una evidente difficoltà a "costruire" e "vedere" mentalmente i fenomeni ed il loro sviluppo consequenziale. Si torna sempre al punto fondamentale: occorre che la mente si abitui fin da bambini a "fare ginnastica" invece che a ingurgitare passivamente solo nozioni.
La frase che ha sottolineato Fabrizio mi affascina, anche per l'uso dell'italiano.