Categorie: Matematica
Tags: bisettrice cerchio corda qualsiasi corde geometria musica quiz relazioni tra corde
Scritto da: Vincenzo Zappalà
Commenti:2
Una nuova media... circolare (con QUIZ trigonometrico) ***
Abbiamo da poco parlato di corde (del cerchio) e di quanto possono essere utili per determinare le aree di figure curvilinee anche molto strane. Nel nostro piccolo, possiamo trovare una relazione tra due corde qualsiasi e la loro corda "media". Una formula semplicissima, all'interno di quella meravigliosa figura geometrica che è il cerchio... Ma voi potreste fare anche di più! Questa volta io mi prendo la parte più semplice e a voi "regalo" la parte più difficile.
Prendiamo un cerchio e tracciamo due corde a e b a partire da un punto P qualsiasi del cerchio. Tracciamo poi la bisettrice dell'angolo tra le due corde. Vogliamo ricavare la lunghezza della corda bisettrice (Fig. 1)
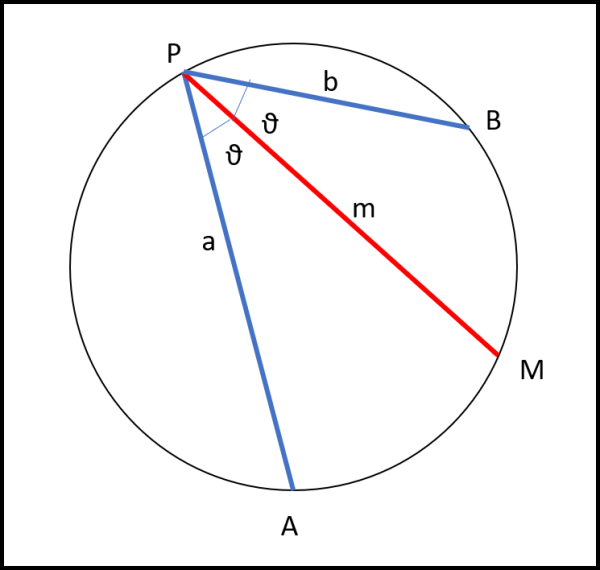
E' sicuramente un gioco molto semplice, ma dovrebbe essere interessante per chi ama la musica e le note. Io sono completamente ignorante in materia e se qualcuno vuole dire qualcosa a proposito è il benvenuto! Occupiamoci, per adesso, solo della parte puramente geometrica...
Sia P il punto da cui tracciare le due corde e la relativa bisettrice. Siano invece A,B e M i corrispondenti punti alle loro estremità opposte. Conoscendo PA = a e PB = b, vogliamo determinare il valore di PM = m. In qualche modo è come volessimo fare una media "particolare" tra PA e PB. L'angolo tra le corde e la bisettrice sia θ.
Agiamo nel modo più intuitivo, congiungendo B con A in Fig. 2.
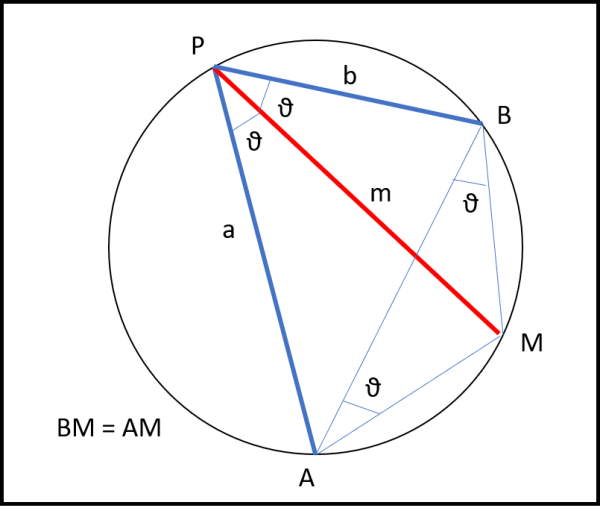
Gli angoli ABM e BAM sono angoli alla circonferenza e devono entrambi essere uguali a θ, dato che devono essere uguali agli angoli APM e BPM, relativi agli stessi archi di circonferenza. Ne segue che il triangolo ABM deve essere isoscele (due angoli uguali) e quindi si ha che:
AM = MB
N.B. : Che AM e MB fossero uguali si poteva anche dedurre dal fatto che i due archi AM e BM sottendono lo stesso angolo al centro (2θ)
L'uguaglianza è quanto basta per considerare separatamente i due triangoli PAM e PBM e applicare ad entrambi il teorema di Carnot,
Dal primo abbiamo:
AM2 = a2 + m2 - 2am cosθ
Dal secondo
BM2 = b2 + m2 - 2bm cosθ
Ma AB2 = BC2
per cui:
a2 + m2 - 2am cos θ = b2 + m2 - 2bm cosθ
Semplificando e raccogliendo:
a2 - b2 = 2m(a - b) cosθ
m = (a2 - b2)/(2(a -b) cosθ)
Ricordando il solito "prodotto notevole" (a2 - b2) = (a + b)(a - b), si ha:
m = ((a + b)/2 )(1/cos θ)
In parole molto povere, non dobbiamo fare altro che fare una normale media delle due corde ((a + b)/2) e moltiplicarla per un fattore che va da 1 (θ = 0) a un valore che tende a infinito per θ che tende al valore massimo degenere di 90°.
La relazione la possiamo vedere molto bene, costruendo due triangoli rettangoli "ad hoc"...
Prolunghiamo, in Fig. 3, la corda m e poi da A tracciamo un segmento perpendicolare ad a che incontri il prolungamento in K. Facciamo lo stesso a partire da B con il punto d'incontro in H.
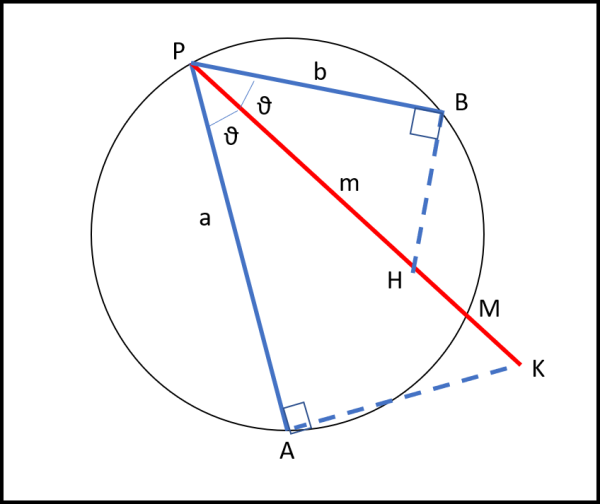
Ci vuol poco a scrivere che:
PK = a /cosθ
PH = b/cosθ
Facendo la media tra PK e PH otteniamo:
(PK + PM)/2 = ((a + b)/2)(1/cosθ) = m
Da cui risulta chiaro che HM = MK.
ADESSO TOCCA VOI (quiz)
Devo dirvi la verità? Il metodo che ho usato non mi è piaciuto molto e preferisco un approccio diverso. Non solo diverso, ma capace di risolvere il caso generale, ossia con la corda centrale NON bisettrice (vedi Fig. 4).
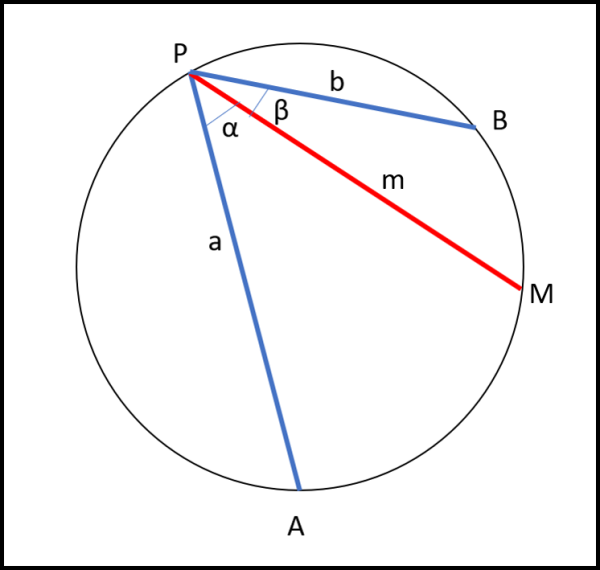
Oltretutto, questo caso potrebbe anche essere più interessante per i musicisti.
Riassumendo: Trovare la relazione che lega la lunghezza della corda c alle due corde a e b e ai due angoli α e β.
P.S.: non cercate nel web e, soprattutto, non fidatevi dei ... cinesi!






2 commenti
A me viene una espressione di questo tipo:
Per trovarla ho introdotto in figura il diametro d che passa per il punto P.
Se chiamo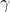 l'angolo tra questo diametro ed m, dovrei avere
l'angolo tra questo diametro ed m, dovrei avere )
Analogamente avrei
Da queste ultime si può ricavare) in funzione di
in funzione di 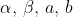 . Nonostante le apparenze è un sistema lineare con due equazioni e due incognite.
. Nonostante le apparenze è un sistema lineare con due equazioni e due incognite.
Che sostituita nella espressione precedente di m porta al risultato.
Bene Fabry,
io l'ho risolto in altro modo... forse ancora più veloce... ma sempre meglio dei ... cinesi (a tempo debito capirai perché... )
)